Содержание водяного пара в воздухе называют влажностью воздуха. Основные характеристики влажности — это упругость водяного пара и относительная влажность.

Водяной пар, как всякий газ, обладает упругостью (давле­нием).

Упругость водяного пара е пропорциональна его плотно­сти (содержанию в единице объема) и его абсолютной темпера­туре. Она выражается в тех же единицах, что и давление воздуха, т. е. либо в миллиметрах ртутного столба, либо в мил­либарах.

Упругость водяного пара в состоянии насыщения называют упругостью насыщения Е. Это максимальная упругость водяного пара, возможная при данной температуре. Например, при тем­пературе 0° упругость насыщения равна 6,1 мб. На каждые 10° температуры упругость насыщения увеличивается примерно вдвое.

Если воздух содержит водяного пара меньше, чем нужно для насыщения его при данной температуре, можно определить, на­сколько воздух близок к состоянию насыщения. Для этого вы­числяют относительную влажность f. Так называют отношение фактической упругости е водяного пара, находящегося в воз­духе, к упругости насыщения Е при той же температуре, выра­женное в процентах, т. е.

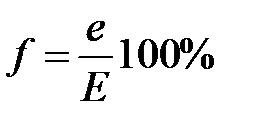
Упругость водяного пара у земной поверхности меняется от сотых долей миллибара (при очень низких температурах зимой в Антарктиде и в Якутии) до 35 мб и более (у экватора). Чем теплее воздух, тем больше водяного пара может он содержать без насыщения и, стало быть, тем больше может быть в нем упругость водяного пара.

Относительная влажность воздуха может принимать все зна­чения от нуля для вполне сухого воздуха (е = 0) до 100% для состояния насыщения (е = Е).

Уравнение состояния газов

Основными характеристиками физического состояния газа являются его давление, температура и плотность. Эти три характеристики не независимы одна от другой. Газы сжимаемы; поэтому плотность их меняется в широких пределах в зависимости от давления и, кроме того, зависит от темпера­туры.

Связь между давлением, температурой и плотностью для идеальных газов дается уравнением состояния газов, известным из физики:

ρ = р /RT,

где р – давление, Т – температура по абсолютной шкале (К), R – газовая постоянная, зависящая от природы газа.

Уравнение состояния газов с достаточным приближением применимо и к сухому воздуху, и к водяному пару, и к влаж­ному воздуху. В каждом случае будет своя величина газовой постоянной R . Для влажного воздуха R меняется в зависимости от упругости водяного пара, содержащегося в воздухе.

Остановимся на указанных основных характеристиках состо­яния применительно к воздуху.

Атмосферное давление

Всякий газ производит давление на ограничивающие его стенки, т. е. действует на эти стенки с какой-то силой давления, направленной перпендикулярно (нормально) к стенке. Число­вую величину этой силы давления, отнесенную к единице пло­щади, и называют давлением. Давление газа объясняется дви­жениями его молекул. При возрастании температуры и при сохранении объема газа скорости молекулярных движений увеличиваются и, следовательно, давление растет.

Если мысленно выделить какой-то объем внутри атмосферы, то воздух в этом объеме испытывает давление извне на во­ображаемые стенки, ограничивающие данный объем, со стороны окружающего воздуха. Со своей стороны воздух изнутри объ­ема оказывает такое же давление на окружающий воздух.

Выделенный объем может быть сколь угодно малым и в пределе сводится к точке. Таким образом, в каждой точке атмо­сферы имеется определенная величина атмосферного давления, или давления воздуха.

С высотой атмосферное давление быстро убывает.

В настоящее время в метеорологии давление выражают в абсолютных единицах — миллибарах (мб). Один миллибар есть давление, которое сила в 1000 дин производит на площадь в один квадратный сантиметр. Среднее атмосферное давление на уровне моря —760 мм рт. ст. — близко к 1013 мб, а 750 мм рт. ст. эквивалентны 1000 мб. Таким образом, для перехода от величины давления в миллиметрах ртутного столба к величине в миллибарах нужно давление в миллиметрах ртутного столба умножить на 4/3; для обратного перехода нужно ввести множи­тель 3/4.

Температура воздуха

Воздух, как и всякое тело, всегда имеет температуру, от­личную от абсолютного нуля. Температура воздуха в каждой точке атмосферы непрерывно меняется; в разных местах Земли в одно и то же время она также различна.

Температура воздуха, а также почвы и воды в большин­стве стран выражается в градусах международной температур­ной шкалы, или шкалы Цельсия (°С), общепринятой в физиче­ских измерениях. Нуль этой шкалы приходится на температуру, при которой тает лед, а +100° — на температуру кипения воды (то и другое при давлении 760 мм рт. ст., близком к фактически существующим на уровне моря условиям). Однако во многих странах употребительна шкала Фаренгейта (F). В этой шкале интервал между точками таяния льда и кипения воды разделен на 180°, причем точке таяния льда приписано значение +32°. Таким образом, величина одного градуса Фарен­гейта равна 5/9°С, а нуль шкалы Фаренгейта приходится на -17,8° С. Нуль шкалы Цельсия соответствует +32° F, a +100°C = +212°F.

Кроме того, в теоретической метеорологии применяется абсолютная шкала температуры (шкала Кельвина, К). Нуль этой шкалы отвечает полному прекращению теплового движе­ния молекул, т. е. самой низкой возможной температуре.

Один кельвин равен 1/273.16 расстояния от абсолютного нуля до тройной точки воды (состояния, при котором лёд, вода и водяной пар находятся в равновесии).

По шкале Цельсия это будет -273,18±0,03°. Но на практике за абсолютный нуль принимается - 273° С. Величина градуса абсолютной шкалы равна величине градуса шкалы Цельсия. Поэтому нуль шкалы Цельсия соответствует 273°

Плотность воздуха

Плотность воздуха непосредственно не измеряется: она вычисляется с помощью уравнения состояния газов. Применяя уравнение состояния газов к сухому воздуху, сле­дует ввести числовое значение газовой постоянной для сухого воздуха R_d , равное 2,87*10⁶, если плотность ρ в г/см³ и давление р в дин/см². Тогда уравнение со­стояния Менделеева—Клапейрона ρ = р / R_d T  даст плотность сухого воздуха.

Найдем теперь выражение для плотности влажного воздуха с температурой Т, давлением р и упругостью водяного пара е. Можно представлять влажный воздух как смесь сухого воздуха и водяного пара. Из общего давления воздуха р на долю сухого воздуха приходится давление р — e . Следовательно, для этой части смеси, для сухого воздуха, уравнение состояния напишется так:

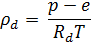
Для водяного пара, находящегося в смеси, уравнение состоя­ния напишется

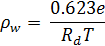
где множитель 0,623 представляет собой отношение плотностей водяного пара и сухого воздуха. Так как общая плотность влаж­ного воздуха ρ' равна сумме плотностей сухого воздуха и водяного пара ρ _d + ρ _w, то уравнение состояния для влажного воздуха окончательно напишется так:

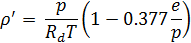
Это и будет выражение для плотности влажного воздуха. Не забудем, что R_d здесь — газовая постоянная для сухого воздуха.

Вследствие малости отношения е/р можно с достаточной точностью приближенно написать, что

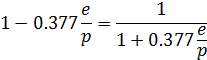
тогда уравнение состояния для влажного воздуха примет вид

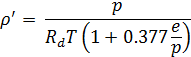
Назовем функцию от температуры, давления и упругости пара Т( 1+0,377∙e / p) виртуальной температурой T_v . Тогда можно написать

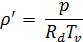
т. е. плотность влажного воздуха выражается уравнением со­стояния для сухого воздуха, но только с заменой истинной тем­пературы на виртуальную. Отсюда можно сказать, что виртуаль­ная температура - это температура T_v , которую должен был бы иметь сухой воздух, чтобы его плот­ность равнялась плотности данного влажного воздуха с темпе­ратурой Т, давлением р и упругостью пара е. Виртуальная температура всегда несколько выше истинной температуры влажного воздуха.

Из уравнения 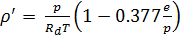видно, что влажный воздух несколько менее плотен, чем сухой воздух при тех же значениях давления и температуры. Это объясняется тем, что водяной пар менее плотен, чем сухой воздух. Если взять какой-то объем сухого воздуха и заменить часть молекул постоянных газов более лег­кими молекулами водяного пара в том же количестве и с теми же скоростями движения так, что температура и давление от этого не изменятся, плотность полученного влажного воздуха будет несколько меньше, чем плотность сухого воздуха. В этом и состоит смысл данного уравнения.

Плотность воздуха в каждом месте непрерывно меняется во времени. Кроме того, она сильно меняется с высотой, потому что с высотой меняются также атмосферное давление и темпе­ратура воздуха. Давление с высотой всегда уменьшается, а вме­сте с ним убывает и плотность. Температура с высотой по боль­шей части понижается, по крайней мере в нижних 10—15 км атмосферы. Но падение температуры влечет за собой повышение плотности. В результате совместного влияния изменения давле­ния и температуры плотность с высотой, как правило, понижа­ется, но не так сильно, как давление.

Если бы плотность воздуха не менялась с высотой, а оста­валась на всех уровнях такой же, как у земной поверхности, то для высоты атмосферы получилась бы величина около 8000 м. В самом деле, приземная плотность сухого воздуха при давле­нии 760 мм и температуре 0° равна 1293 г/м³; столб воздуха с этой плотностью должен был бы иметь высоту, очень близкую к 8000 м , чтобы производить такое же давление, какое произво­дит столб ртути в 760 мм высотой (1033 г/см³). Указанная высота (8000 м) называется высотой однородной атмосферы. В действительности плотность воздуха с высотой убывает, и по­тому истинная высота атмосферы равняется многим тысячам километров.