Теперь поставим вопрос: по какому закону меняется ат­мосферное давление с высотой? Допустим, что известно давле­ние на одном уровне. Каково оно в тот же момент на другом, выше- или нижележащем уровне?

Возьмем вертикальный столб воздуха с поперечным сече­нием, равным единице, и выделим в этом столбе бесконечно тонкий слой, ограниченный снизу поверхно­стью на высоте z , а сверху — поверхностью на высоте z + dz ; толщина слоя, таким образом, dz (Рис. 3). На нижнюю поверх­ность выделенного элементарного объема смежный воздух действует с силой давления, направленной снизу вверх; величина этой силы на рассматриваемую поверхность с площадью, равной единице, и будет давле­нием воздуха р на этой поверхности. На верхнюю поверхность элементарного объе­ма смежный воздух действует с силой дав­ления, направленной сверху вниз. Числовая величина этой силы p + dp есть давление на верхней границе. Это давление отличается от давления на нижней границе на бесконечно малую вели­чину dp , причем заранее не известно, будет ли dp положитель­ным или отрицательным, т. е. будет ли давление на верхней границе выше или ниже, чем на нижней границе.

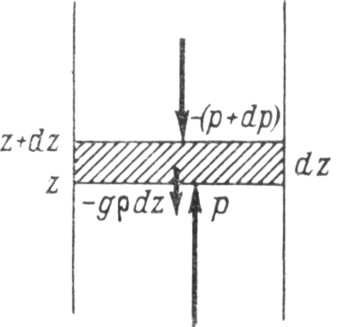
Рис. 3. Силы, действующие на элементарный объем воздуха

Что касается сил давления, действующих на боковые стенки объема, то допустим, что в горизонтальном направлении атмо­сферное давление не меняется. Это значит, что силы давления, действующие со всех сторон на боковые стенки, уравновешива­ются; их равнодействующая равна нулю. Отсюда следует, что воздух в горизонтальном направлении не обладает ускорением и не перемещается.

Кроме того, воздух в рассматриваемом элементарном объеме испытывает силу тяжести, которая направлена вниз и равна ускорению силы тяжести g , умноженному на массу воздуха во взятом объеме. Так как при поперечном сечении, равном единице, объем равен dz , то масса воздуха в нем равна ρ*dz , где ρ — плотность воздуха, а сила тяжести равна g ρ dz . Допустим, что в атмосфере суще­ствует равновесие также и в вертикальном направлении, т. е. что взятый объем воздуха не имеет никакого ускорения также и по вертикали и, таким образом, остается на одном и том же уровне, несмотря на наличие веса. Это значит, что сила тяжести (вес) и силы давления уравновешиваются. Вниз направлены сила давления p + dp и вес g ρ dz ; возьмем их с отрицательным знаком. Вверх направлена сила давления р, которую возьмем с положительным знаком. Сумму всех этих трех сил приравняем к нулю и, таким образом, получим

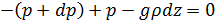
или

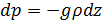
Отсюда следует, что при положительном dz имеем отрица­тельное dp , т. е. что с высотой атмосферное давление падает. При этом разность давлений на нижней и верхней границах рассматриваемого элементарного объема равна весу воздуха в этом объеме.

Уравнение 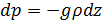 носит название основного уравнения статики атмосферы. Это дифференциальное уравнение говорит о том, как меняется давление при бесконечно малом приросте высоты.

Основное уравнение статики можно написать еще так:

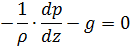
Величина –dp / dz - падение давления на единицу прироста высоты, т. е. вертикальный барический градиент (вертикальный градиент давления). Это равнодействующая сил давления, направленных сверху и снизу на единицу нашего объема.

Разделив ее на плотность ρ, мы получим –1/ρ* dp / dz  — силу верти­кального барического градиента, отнесенную к единице массы и направленную вверх.

Второй член — это сила тяжести, действующая на ту же еди­ницу массы и направленная вниз. Она равна силе барического градиента, но направлена в противоположную сторону. Следова­тельно, основное уравнение статики выражает условие равнове­сия между двумя силами, действующими на единицу массы воз­духа по вертикали, — силой вертикального барического гради­ента и силой тяжести.

Чтобы получить выражение для изменения давления при конечном приросте высоты, нужно уравнение проинтегрировать в пределах от уровня z ₁ с давлением р₁ до вышележа­щего уровня z ₂ с давлением р₂. При этом плотность воздуха р является переменной величиной, функцией высоты.

В конце концов, получим формулу

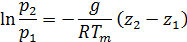
Потенциируя ее, получим

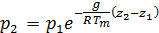
Это уравнение представляет собой интеграл основ­ного уравнения статики атмосферы. Его называют еще баромет­рической формулой высоты. Эта формула показывает, как ме­няется атмосферное давление с высотой в зависимости от температуры воздуха.

Выше было показано, что бесконечно малая разность давле­ний равна весу элементарного объема воздуха с толщиной dz . Следовательно, и конечная разность давлений между нижним и верхним уровнем равна весу воздушного столба между этими уровнями. Если за верхний уровень принять верхнюю границу атмосферы, на которой давление практически равно нулю, то очевидно, что давление на любом уровне равно весу всего столба атмосферы, простирающегося над данным уровнем.

Основное уравнение статики выводится в предположении равновесия воздуха по вертикали. В действительности может су­ществовать какая-то равнодействующая сил тяжести и верти­кального барического градиента, отличная от нуля. Но, как правило, эта равнодействующая незначительна, и, стало быть, ускорение, сообщаемое ею воздуху, мало. Основное уравнение статики будет при этом выполняться не абсолютно строго, но с большой степенью точности.