Не двоичные счетчики – это счетчики, у которых M≠2n, где n – число разрядов, а М – число состояний.
Существует два подхода к реализации таких счетчиков:
1) За основу берут сразу не двоичный счетчик.
2) За основу берут двоичный счетчик и удаляют лишние состояния.
К не двоичным счетчикам относят: полиноминальные, счетчики Джонсона и др.
Из двоичных счетчиков не двоичные получают методом блокировки переноса или методом принудительного насчета.
Рассмотрим не двоичные счетчики на примере двоично-десятичного счетчика (модуль счета 10).
В двоично-десятичном коде одна десятичная цифра представлена четырьмя двоичными разрядами. Эти четыре разряда называют тетрадой или декадой.
| Цифра | Тетрада | ||||
| 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 2 | 0 | 0 | 1 | 0 | |
| 3 | 0 | 0 | 1 | 1 | |
| 4 | 0 | 1 | 0 | 0 | |
| 5 | 0 | 1 | 0 | 1 | |
| 6 | 0 | 1 | 1 | 0 | |
| 7 | 0 | 1 | 1 | 1 | |
| 8 | 1 | 0 | 0 | 0 | |
| 9 | 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 |
| |
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | ||
| 1 | 1 | 1 | 0 | ||
| 1 | 1 | 1 | 1 | ||
За основу берут сразу не двоичный счетчик.
Полиноминальные счетчики.
Полиноминальными счетчиками называют пересчетные схемы, получаемые на основе сдвигающих регистров, в которые заведены обратные связи через сумматоры по модулю 2. Часто используют для получения псевдослучайной последовательности чисел.
Сумматор по модулю 2:
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Условное графическое обозначение:
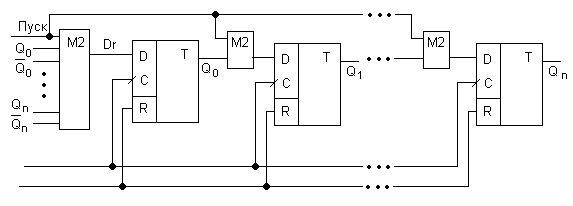
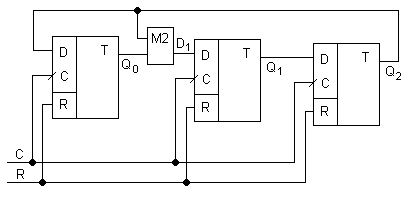
Двухвходовые сумматоры на входе D используются лишь в начальный момент для установки начального кода. На вход триггера Q0 устанавливается многовходовой сумматор, на вход которого заводят прямые или инверсные выходы триггеров. Количество разрядов которые заводят на вход М2 не регламентируются (может быть 1, а может и n+1). Если на вход М2 заводятся только прямые значения Q или четное количество инверсных, то счетчику обязательно требуется сигнал «Пуск». Если число инверсных входов не четно, то сигнал «Пуск» не обязателен, а тогда не нужны и двухвходовые сумматоры по модулю 2.
Многовходовой сумматор дополнительно может быть установлен и на входы других разрядов, не только Q0. В стандартном полиноминальном счетчике на вход многовходового сумматора М2 заводят только прямые значения Q и начальная установка такого счетчика состоит из двух этапов:
- В начале подают сигнал R, который сбрасывает все триггера и счетчик получает значение 0000. В этом состоянии он может находиться сколь угодно долго.
- Далее на один такт сигнала С подается сигнал «Пуск». И в те разряды, куда заведен сигнал «Пуск» вдвинется 1. Во время работы сигнал «Пуск» равен 0. При этом получаем обычный сдвиговый регистр, только на вход Dr заведена сумма разрядов.
Пример: Стандартный счетчик на 7 состояний.
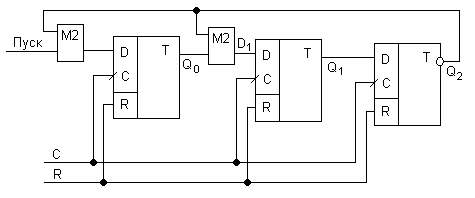
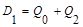
| Q2 | Q1 | Q0 | D1 | Пуск | ||
| 0 | 0 | 0 | 0 | 1 | ||
 0 0
| 0 | 1 | 1 | 0 | ||
| 0 | 1 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | 0 | ||
| 1 | 1 | 1 | 0 | 0 | ||
| 1 | 0 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 1 | 0 |
М=7 (модуль счета)
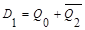
| Q2 | Q1 | Q0 | D1 |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
М=7 (модуль счета)
Если полиноминальный счетчик имеет 2n-1 состояний и одно состояние – начальное устойчивое, то его называют генератор псевдослучайной последовательности.
Дата: 2019-02-25, просмотров: 531.
 запрещенные
запрещенные