Дешифратор – это комбинационный узел, преобразующий двоично-позиционный код в код 1 из N. Код 1 из N содержит одну и только одну 1, остальные комбинации запрещенные.
Условное графическое обозначение:
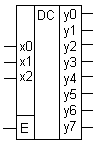
Е – вход разрешения работы.
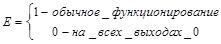
Если дешифратор имеет инверсные выходы, то и вход Е тоже инверсный.
Для дешифратора справедливо выражение: n = 2m, где n – число выходов, а m – число входов.
Классификация дешифраторов:
В зависимости от количества выходов дешифраторы разделяют на:
· Полные (n=2m)
· Не полные (n<2m)
А по внутренней структуре дешифраторы делят на:
· Линейные (параллельные, прямоугольные)
· Пирамидальные
Т.к. дешифратор комбинационный узел, то его можно описать таблицей истинности:
| E | x2 | x1 | x0 | y0 | y1 | y2 | y3 | y4 | y5 | y6 | y7 |
| 0 | * | * | * | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
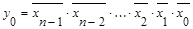
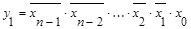
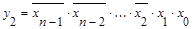
. . .
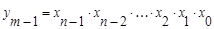
Приведенная система переключательных функций описывает работу дешифратора.
Линейный дешифратор.
В линейном дешифраторе непосредственно реализуется система переключательных функций, с помощью которой описывается его функционирование.
Пример: 2 в 4 (2 входа и 4 выхода)
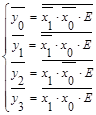
Реализуем дешифратор с инверсными выходами:
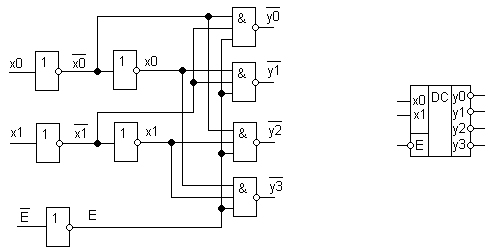
Два инвертора подряд установлены по той же причине, что и у мультиплексора.
Особенности схемы:
1) Линейный дешифратор имеет максимальное быстродействие
2) С увеличением количества выходов:
· Увеличивается число входов у элементов «И-НЕ»
· Возрастает нагрузка на вход инвертора
Дешифратор 1 в 2 имеет следующий вид:
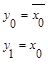
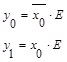
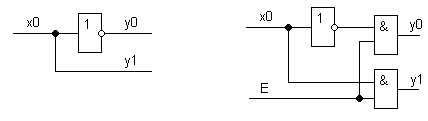
Наращивание разрядности дешифратора.
Существует два способа наращивания:
· Прямоугольный
· Пирамидальный
Пирамидальное наращивание:
Дешифратор строится как многоярусная схема.
Рассмотрим на примере: пусть необходимо построить дешифратор 4 в 16 на основе дешифраторов 2 в 4.
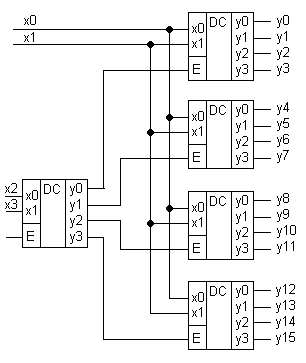
Количество ярусов не ограниченно, число дешифраторов текущего яруса определяется – количеством выходов в предыдущем.
Если при наращивании использовать дешифратор 1 в 2, и представить его на логических элементах, то получают пирамидальный дешифратор, который имеет более низкое быстродействие, по сравнению с линейным, но лишен его недостатков.
Прямоугольное наращивание:
Построим дешифратор 4 в 16 на основе 2 в 4:
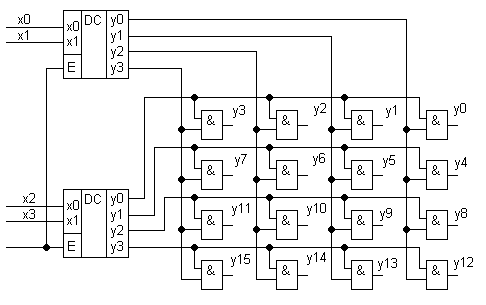
На схеме представлен первый уровень прямоугольного наращивания, но если её сдублировать, то для двух схем можно построить ещё один уровень прямоугольного наращивания и т.д.
Матрица из элементов «И» называется матричным дешифратором.
Если на первом уровне все дешифраторы представить как 1 в 2, причем на логических элементах, то получим прямоугольный дешифратор, обладающий особенностями подобным пирамидальному.
Дата: 2019-02-25, просмотров: 666.