Мультиплексор может быть использован в качестве программируемого универсального логического модуля. Подавая на его информационные входы 0 и 1, можно воспроизвести произвольную функцию от аргументов, поступающих на управляющие входы.
1. Анализ схемы мультиплексора.
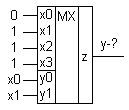
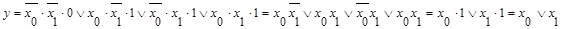
2. Синтез схемы.
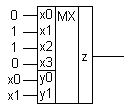
Для воспроизведения функции от числа аргументов, превышающего число входов мультиплексора, используют многоярусную схему.
Предположим, у нас дана функция:
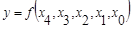
А у нас есть мультиплексор только с двумя и тремя входами управления.
По теореме Шеннона получаем:
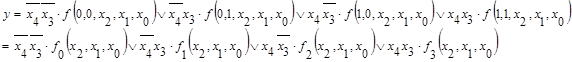
f 0 , f 1 , f 2 , f 3 – можно реализовать на четырех мультиплексорах 8 в 1.
Вид выражения соответствует функции описывающей работу мультиплексора 4 в 1.
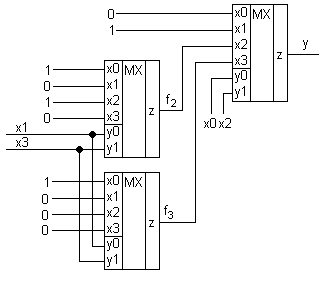
В результате получаем двухъярусную схему:
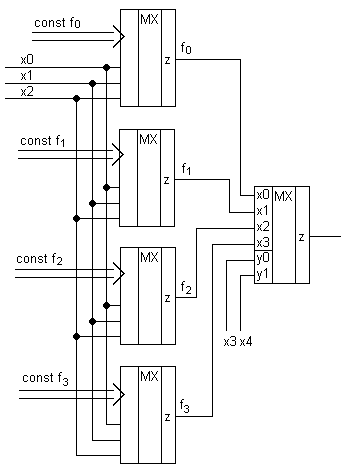
Пусть у нас функция x 3 , x 2 , x 1 , x 0 , а мультиплексор только 4 в 1.
| x 3 | x 2 | x 1 | x 0 | y | |
| 0 | 0 | 0 | 0 | 0 | f 0 |
| 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 1 | f 1 |
| 0 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | f 2 |
| 1 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 1 | f 3 |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 |
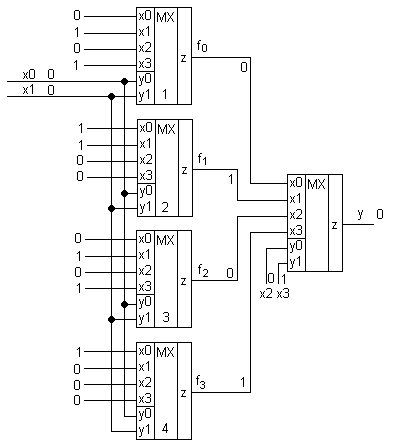
В методичках такая схема называется константа мультиплексора.
В нашем случае получилось, что f 0 = f 2 это значит, что два мультиплексора работают параллельно и один из них можно удалить. Допустим, удалим первый мультиплексор, а вход третьего мультиплексора подадим на x 2 и x 0 .
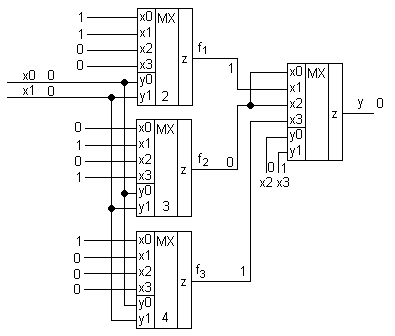
На структуре из пяти мультиплексоров можно реализовать любую функцию четырёх аргументов. Для этого достаточно лишь установить соответствующие константы на входы мультиплексоров первого яруса.
Если f i =0 или 1, либо f i = f j , то число мультиплексоров в первом ярусе уменьшается. Добится таких ситуаций можно путем перераспределения аргументов функции между входами мультиплексоров различных ярусов. Это перераспределение удобно выполнять по картам Карно.
| x 1 | 1. f0: x2=0; x0=0 | ||||||
| x 0 | 2. f1: x2=0; x0=1 | ||||||
| 0 | 1 | 1 | 0 | 3. f2: x2=1; x0=0 | |||
| 1 | 1 | 0 | 0 | 4. f3: x2=1; x0=1 | |||
| 1 | 0 | 0 | 0 | ||||
| x 3 | x 2 | 0 | 1 | 1 | 0 |
| f0: | x1 | f1: | x1 | |||||||
| 0 | 0 | ® f0=0 | 1 | 1 | ® f1=1 | |||||
| x3 | 0 | 0 | x3 | 1 | 1 | |||||
| f2: | x1 | f3: | x1 | |||||||
| 1 | 0 | ® f2 ¹ const | 1 | 0 | ® f3 ¹ const; f3 ¹ f2 | |||||
| x3 | 1 | 0 | x3 | 0 | 0 |
Если у мультиплексора не хватает всего одного входа, то функция fi будет зависеть от одной переменной. Множество таких функций не велико: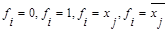 
. Следовательно, в худшем случае, вместо первого яруса мультиплексора понадобиться всего один инвертор.
Реализуем исходную функцию четырех переменных на мультиплексоре 8 в 1, у которого не хватает всего одного входа:
| x1 | |||||||
| x0 | |||||||
| 0 | 1 | 1 | 0 | ||||
| 1 | 1 | 0 | 0 | ||||
| 1 | 0 | 0 | 0 | ||||
| x 3 | x2 | 0 | 1 | 1 | 0 | ||
| x0 | |||||||
| f0: | 0 | 1 |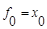 
| ||||
| x0 | |||||||
| f1: | 0 | 1 |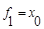 
| ||||
| x0 | |||||||
| f2: | 1 | 1 |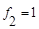 
| ||||
| x0 | |||||||
| f3: | 0 | 0 |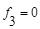 
| ||||
| x0 | |||||||
| f4: | 0 | 1 |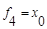 
| ||||
| x0 | |||||||
| f5: | 0 | 1 |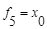 
| ||||
| x0 | |||||||
| f6: | 1 | 0 |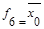 
| ||||
| x0 | |||||||
| f7: | 0 | 0 |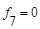 
|
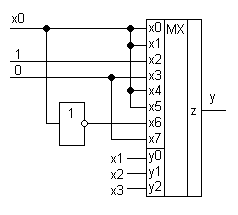
Даже в случае если не хватает двух входов, реализация fi может оказаться более простой на логических элементах, чем использовать ярус мультиплексора. Схема явно будет проще, если все fi содержат либо константы. Либо по две 1, которые склеиваются между собой. Самая сложная схема получается, если fi содержит две единицы, которые не склеиваются.
| x1 | ||||||
| x0 | ||||||
| 0 | 1 | 1 | 0 | |||
| 1 | 1 | 0 | 0 | |||
| 1 | 0 | 0 | 0 | |||
| x3 | x2 | 0 | 1 | 1 | 0 | |
| ||||||
| ||||||
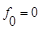
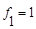
| f2: | x1 | |||||
| 1 | 0 | |||||
| x3 | 1 | 0 | ||||
| ||||||
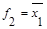
| f3: | x1 | |||||
| 1 | 0 | |||||
| x3 | 0 | 0 | ||||
|
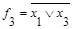
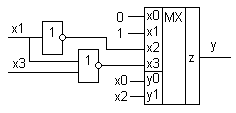
На основе мультиплексора можно построить программируемый модуль для реализации комбинационных узлов, если на информационные входы установить регистр, в который программным образом записывать константы 0 и 1. При изменении констант, меняется функция описывающая узел.
Дата: 2019-02-25, просмотров: 287.
