Функция pdesolve позволяет решать дифференциальные уравнения и системы, в которые не входят уравнения , содержащие производную по t выше первой степени. Однако в любых гиперболических уравнениях есть вторая производная по t. Поэтому, чтобы решить гиперболическое уравнение, нужно его преобразовать в систему дифференциальных уравнений в частных производных, введя дополнительную функцию .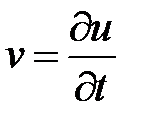

Задача 2

Найти решение начально-краевой задачи для гиперболического уравнения:

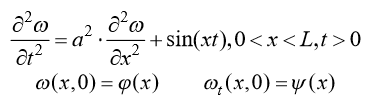
Решение:

Введем дополнительную функцию:

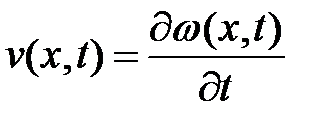
и таким образом сведем гиперболическое уравнение к системе дифференциальных уравнений в частных производных:

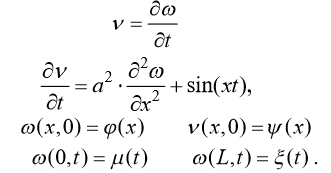
Будем решать эту систему с помощью блока Given-Pdesolve. Первым параметром в функции pdesolve будет массив имен функций, т.е. 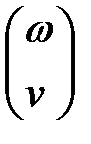. Результатом выполнения функции pdesolve будет вектор функция 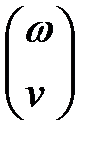, представляющая решение системы.

Ниже приведен пример решения задачи для гиперболического уравнения в Mathcad.

Определяем функции Φ(х), ψ(x), ξ(t), ?(t)

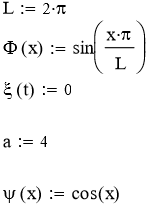
Задаем уравнения и граничные условия:

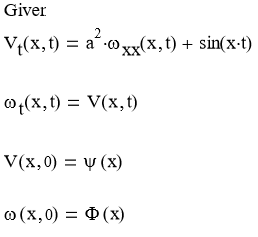
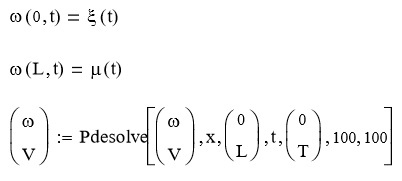
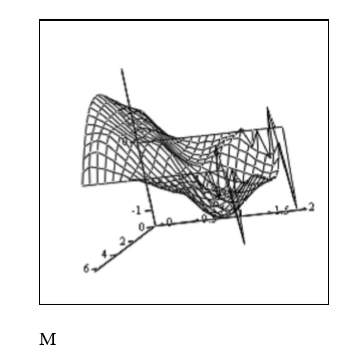
Строим график решения:

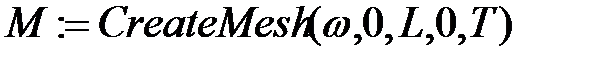
ПЕРЕЧЕНЬ РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ

1. Осиновская, И.В. Численные методы решения алгебраических уравнений и их систем [Электронный ресурс]: электрон, учеб. пособие / И. В. Осиновская, А.Г. Шляпугин, Я. А. Ерисов; Минобрнауки России, Самар, гос. аэрокосм, ун-т им. С. П. Королева (нац. исслед. ун-т). - Электрон, текстовые и граф. дан. (1,41 Мбайт). - Самара, 2012. - 1 эл. опт. диск (CD-ROM).

2. Конспект лекций по дисциплине «Численные методы и моделирование» для студентов направлений подготовки 6.050202 «Автоматизация и компьютерно- интегрированные технологии», 6.092501 «Автоматизированное управление технологическими процессами» / сост. А. А. Костиков. – Краматорск, ДГМА, 2012. – 55с.

3. Макаров, Е. Г. Инженерные расчеты в Mathcad: учебный курс/Макаров Е.Г. — СПб: Питер. 2005 — 448 с.: ил.

4. Вержбицкий В. М. Основы численных методов. - М.: Высшая школа, 2002.

5. Волков Е. А. Численные методы. - СПб.: Лань, 2004.

6. Самарский А. А. Введение в численные методы. - М.: Наука, 1987.

7. Самарский А. А., Гулин А. В. Численные методы. - М.: Наука, 1989.

8. Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной алгебры. - М.: Физматгиз, 1960.

9. Конспект лекций по дисциплине « Информатика». Основы работы с пакетом прикладных программ MatchCAD по разделу «Численные методы решения прикладных задач с помощью пакета MatchCAD: для студентов технических специальностей / Сост.: А.А. Гончаров, Л.В. Васильева.- Краматорск: ДГМА, 2003.-44с.

10. Сборник задач по методам вычислений/Под ред. П. И. Монастырного.- М.: Наука, 1994.

КОНСПЕКТ ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ

"Численные методы"

(для студентов направления подготовки 15.03.04 «Автоматизация технологических процессов и производств» по профилю «Автоматизированное управление технологическими процессами» и специальности 21.05.04 «Горное дело», специализация №10 очной, очно-заочной и заочной форм обучения)

Уровень образования: бакалавриат, специалитет

Составители:                                                         А.Е. Ткаченко