Если приближенное число содержит лишние (или неверные знаки), то его следует округлить. При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причем:

- Если первая отбрасываемая цифра больше четырех, то последняя сохраняемая цифра увеличивается на единицу

- Если отбрасываемая часть состоит только из цифры 5, то округляют так, чтобы последняя цифра оставалась четной.

П ример 1.4

Округляя число 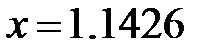 до четырех значащих цифр, определить абсолютную и относительную погрешности полученных приближений.

Решение:

Округлим число 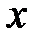 до четырех значащих цифр 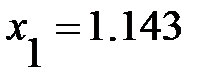. По определению верной цифры абсолютная погрешность числа  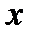равна:

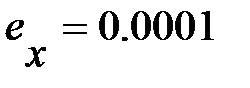. Погрешность округления .

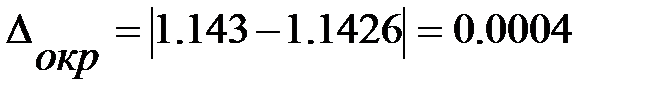Следовательно, погрешность округленного числа 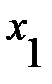 равна:

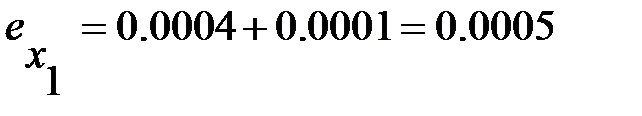. Поэтому абсолютная погрешность равна:

.

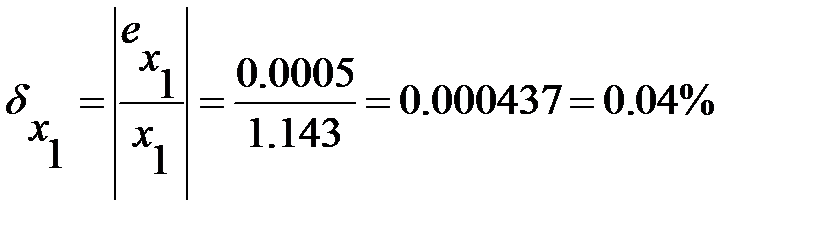Вычислительная погрешность

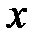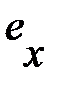Будем обозначать абсолютную погрешность числа  как  , относительную погрешность .

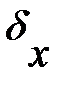Приведем формулы для вычисления погрешностей, возникающих при выполнении арифметических операций над числами х и у.

1) Погрешность суммы

Абсолютная погрешность:

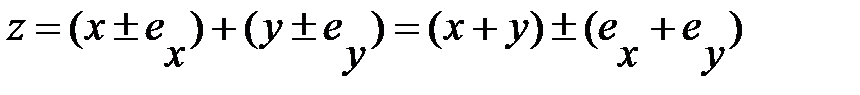
Относительная погрешность:

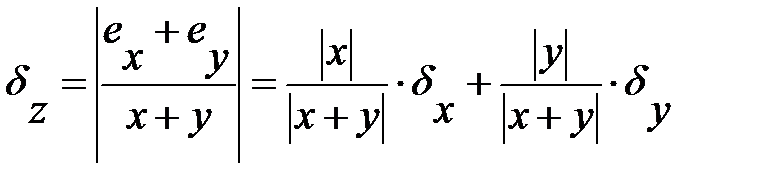
Аналогично определяется погрешность разности.

2) Погрешность произведения

Абсолютная погрешность:

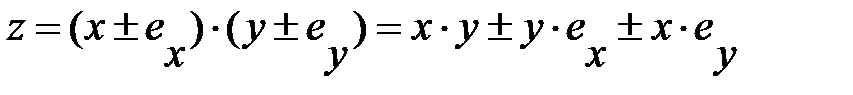
Относительная погрешность:

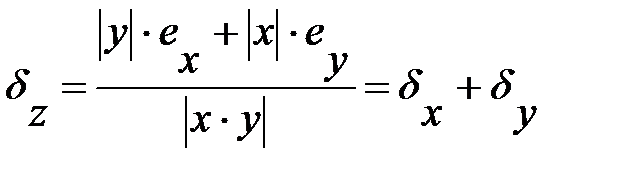
3) Погрешность частного

Абсолютная погрешность:

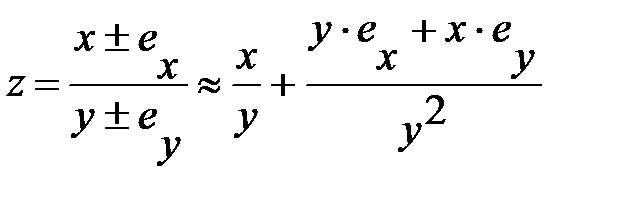
Относительная погрешность:

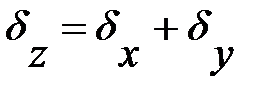
4) Погрешность функции, зависящей от одной переменной

Абсолютная погрешность:

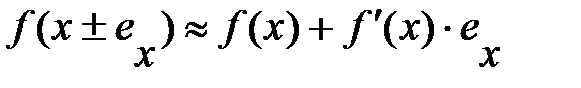
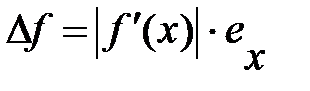
Относительная погрешность:

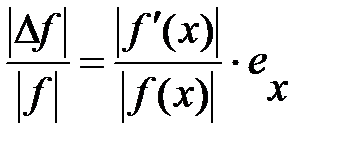
Р Е Ш Е НИЕ УРАВНЕНИЙ С ОДНОЙ ПЕРЕМЕННОЙ.

2.1 О с новные определения.

Нелинейное уравнение имеет вид:

,

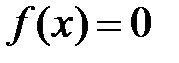где 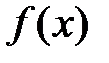 – функция, определенная на участке 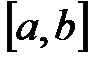. Здесь  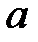и 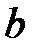 – действительные числа.

Определение 1

Всякое число 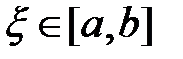, при котором 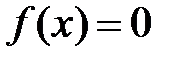, называется корнем уравнения .

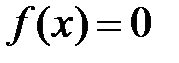Определение 2

Если 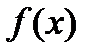 – многочлен, отличный от нулевого, то уравнение называется алгебраическим, иначе – трансцендентным (показательным, логарифмическим, тригонометрическим и т.п.).

Задача приближенного вычисления корней уравнения 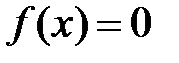 распадается на две:

1) Отделение корней уравнения – процедура нахождения отрезков, на которых уравнение 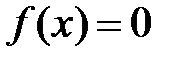 имеет только одно решение.

2) Вычисление корня с заданной точностью .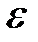

Справедлива следующая теорема:

Теорема Больцано-Коши:

Если непрерывная функция 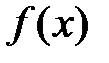 принимает на концах отрезка  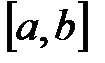значение разных знаков, т.е. 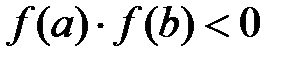, то внутри этого отрезка содержится, по крайней мере, один корень. Этот корень будет единственным, если производная  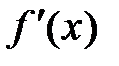существует и сохраняет постоянный знак внутри отрезка .

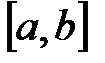Рассмотрим приближенные методы нахождения корней.