Пусть уравнение 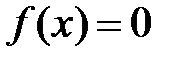 имеет на отрезке
имеет на отрезке 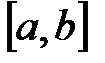 единственный корень и
единственный корень и 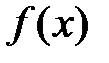 на данном отрезке непрерывна.
на данном отрезке непрерывна.
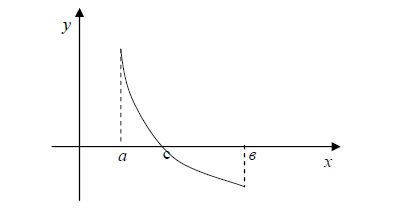
Рисунок 2.1 – Метод половинного деления
Разделим отрезок 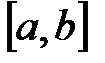 пополам точкой
пополам точкой 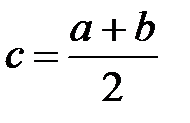 (рис. 2.1).
(рис. 2.1).
Если 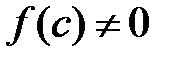 , то возможны два случая:
, то возможны два случая:
1) корень лежит на отрезке 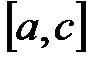
2) корень лежит на отрезке 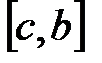 .
.
Если 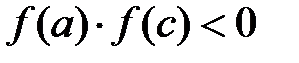 , то корень лежит на отрезке
, то корень лежит на отрезке 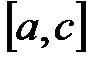 , а если
, а если 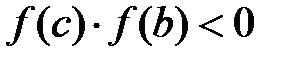 , то корень лежит на отрезке
, то корень лежит на отрезке 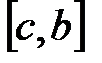 . Выбираем в каждом случае тот отрезок, на котором функция меняет знак и продолжаем процесс половинного деления. В результате получим сколь угодно малый отрезок, содержащий корень уравнения. Блок схема алгоритма половинного деления приведена на рис. 2.2.
. Выбираем в каждом случае тот отрезок, на котором функция меняет знак и продолжаем процесс половинного деления. В результате получим сколь угодно малый отрезок, содержащий корень уравнения. Блок схема алгоритма половинного деления приведена на рис. 2.2.
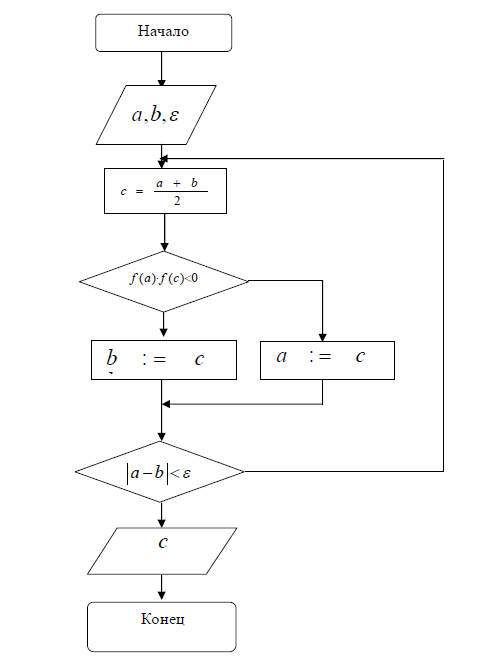
Рис. 2.2 – Блок схема алгоритма метода половинного деления
Рассмотрим пример нахождения корня методом половинного деления в Mathcad.
Пример 2.1
Найти решение уравнения 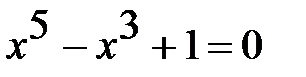 методом половинного деления.
методом половинного деления.
Решение:
1. Определяем функцию 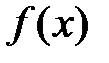 , равную левой части уравнения:
, равную левой части уравнения:
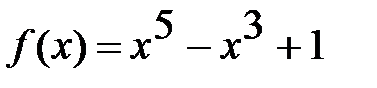
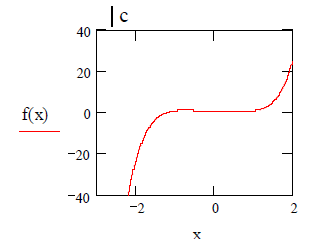
2. Определяем интервал, на котором находится корень уравнения. Для этого строим график функции 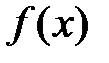 .
.
3. Задаем функцию mpd(a, b, ε), определяющую корень уравнения методом половинного деления. Эта функция имеет следующие аргументы:
a, b – границы интервала, на котором находится корень уравнения, ε – точность вычисления корня.
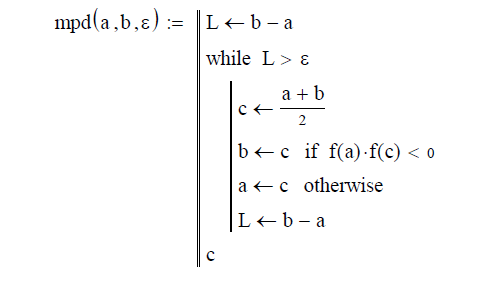
4. Вычисление значения корня:
mpd(–2, 2, 0.01)=1.242
Таким образом, корень уравнения равен –1.242. Из графика видно, что корень уравнения находится на отрезке [–2;2], поэтому границы этого отрезка взяты в качестве параметров a и b функции mpd. Корень найден с точностью ε=0.01.
М е т о д хорд
Вместо деления отрезка 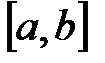 пополам, как в методе половинного деления, делим его в отношении
пополам, как в методе половинного деления, делим его в отношении 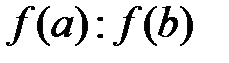 . Таким образом первое приближение корня находится в точке пересечения отрезка
. Таким образом первое приближение корня находится в точке пересечения отрезка 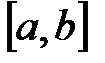 хордой, проходящей через точки с координатами
хордой, проходящей через точки с координатами 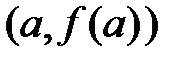 и
и 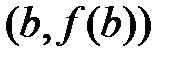 .Если функция меняет знак на отрезке
.Если функция меняет знак на отрезке 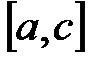 , т.е.
, т.е. 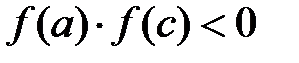 , то корень лежит на отрезке
, то корень лежит на отрезке 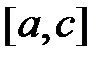 , в противном случае корень лежит на отрезке
, в противном случае корень лежит на отрезке 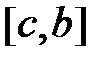 . Выбирая в качестве нового отрезка отрезок
. Выбирая в качестве нового отрезка отрезок 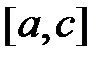 или
или 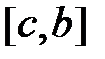 продолжаем процесс до тех пор, пока длина отрезка, на котором находится корень, не станет меньше любого наперед заданного числа
продолжаем процесс до тех пор, пока длина отрезка, на котором находится корень, не станет меньше любого наперед заданного числа 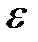 . Точку c находим следующим образом.
. Точку c находим следующим образом.
Запишем уравнение прямой, проходящей через точки с координатами 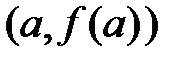 и
и 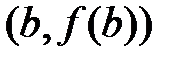 :
:
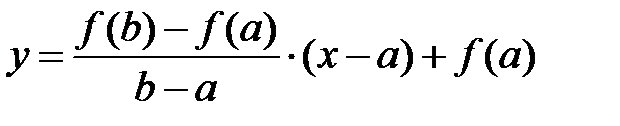
Точка пересечения этой прямой с осью Ох и будет искомой точкой с. Итак,
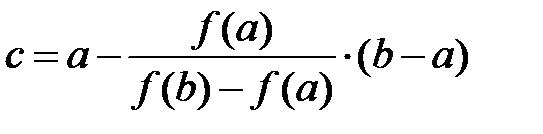
Блок-схема алгоритма метода хорд приведена на рис. 2.3
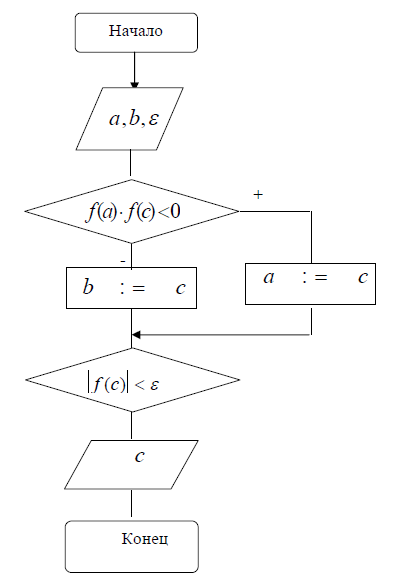
Рис 2.3 – Блок-схема метода хорд
Таким образом, алгоритм метода хорд заключается в следующем:
1. Находим точку с по формуле:
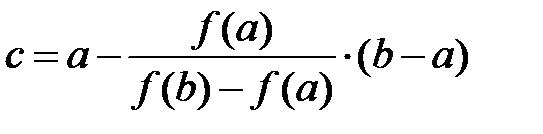
2. Если условие пункта 2 не выполняется, то вычисляем произведение 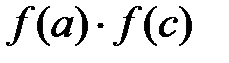 . Если
. Если 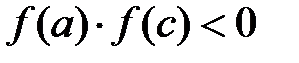 , то полагаем
, то полагаем 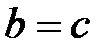 , в противном случае полагаем
, в противном случае полагаем 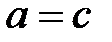 .
.
3. Если 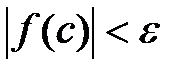 , то завершаем алгоритм. Искомый корень равен с. Корень найден с точностью
, то завершаем алгоритм. Искомый корень равен с. Корень найден с точностью 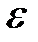 . В противном случае переходим к пункту 1.
. В противном случае переходим к пункту 1.
Рассмотрим пример нахождения корня методом хорд.
Пример 2.2
Найти решение уравнения 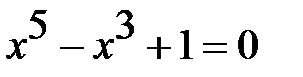 методом хорд.
методом хорд.
Решение:
1. Определяем функцию 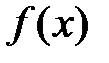 , равную левой части уравнения:
, равную левой части уравнения:
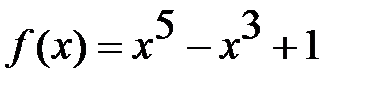
2. Определяем интервал, на котором находится корень уравнения. Для этого строим график функции 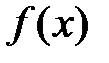 :
:
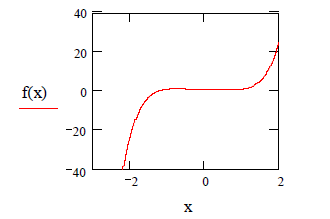
3. Задаем функцию horda(a, b, ε), определяющую корень уравнения методом хорд.
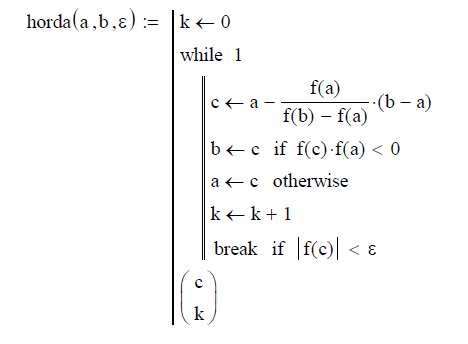
Эта функция имеет следующие аргументы: a, b – границы интервала, на котором находится корень уравнения, ε – точность вычисления корня. Функция horda возвращает значение корня и количество итераций k, необходимое для достижения заданной точности.
Находим корень уравнения с точностью 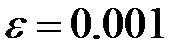 , используя метод хорд:
, используя метод хорд:
horda(–2, –1, 0.001)= 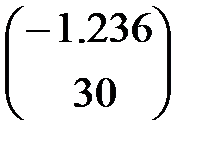
Дата: 2019-02-18, просмотров: 1050.