Будем искать интерполирующую функцию F(x) в виде канонического полинома степени n:
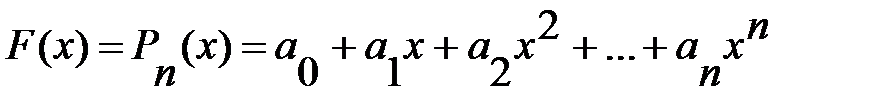(5.2)
Коэффициенты полинома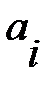 
определяются из условий Лагранжа 
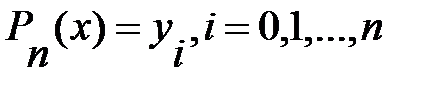, что с учетом выражения (5.2) дает систему линейных уравнений с n+1 неизвестными:
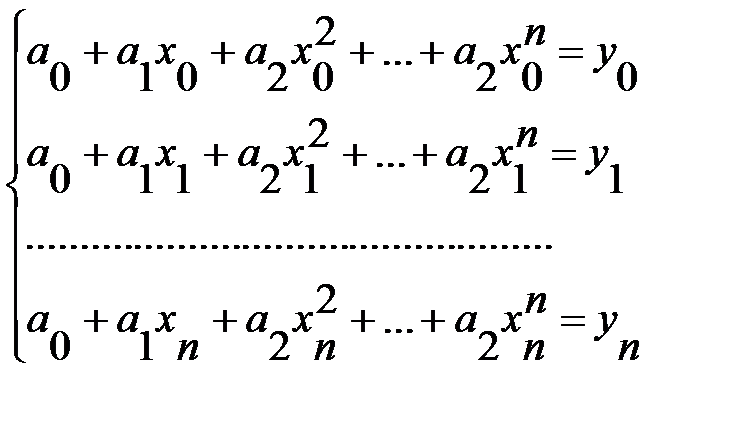(5.3)
Систему уравнений (5.3) можно записать в виде:
, 
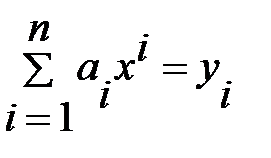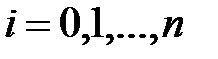
или в матричной форме
C·a=y (5.4)
где a - вектор, содержащий неизвестные коэффициенты полинома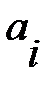 
, y-вектор, содержащий значения функции в узлах интерполяции, 
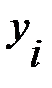, а матрица C имеет вид:
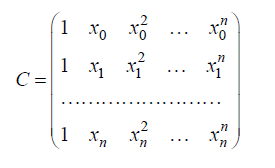
Система линейных алгебраических уравнений имеет единственное решение, если определитель матрицы C отличен от нуля. Этот определитель, называемый определителем Вандермонда, отличен от нуля, если среди узлов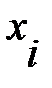 
нет совпадающих.
Решение системы (5.3) в матричном виде имеет вид:
a=C-1·y
где C-1 – обратная матрица (C-1·C=E, E - единичная матрица).
Рассмотрим пример реализации полиномиальной интерполяции в Mathcad.
Пример 5.1
По заданным значениям функции в узлах интерполяции построить канонический полином. Построить график полученного интерполяционного полинома.
Решение
1. Определяем координаты узлов интерполяции:
2. 
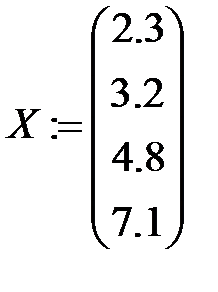
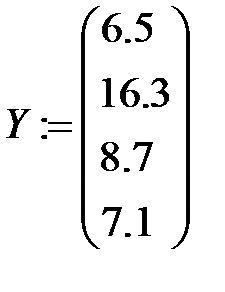
3. Определяем коэффициенты интерполяционного полинома:
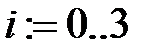
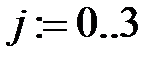
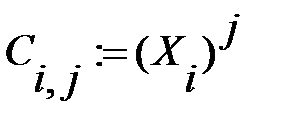
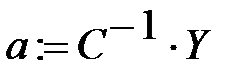
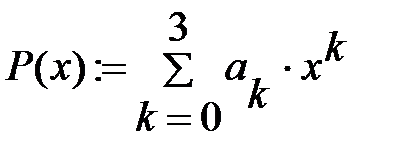
4. Строим график интерполяционной функции:
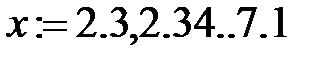
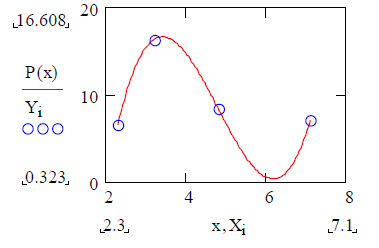
Многоинтервальная интерполяция
Рассмотренная выше полиномиальная интерполяция не всегда дает
удовлетворительные результаты. Несмотря на выполнение условий Лагранжа в узлах, интерполяционная функция может иметь значительное отклонение от аппроксимируемой кривой между узлами.
С увеличением количества узлов возрастает и степень интерполяционного полинома, что приводит к резкому увеличению погрешности в результате возникновения, так называемого явления волнистости. Для того чтобы избежать высокой степени полинома отрезок интерполяции разбивают на несколько частей и на каждом частичном интервале строят самостоятельный полином невысокой степени. Рассмотрим наиболее часто используемые виды многоинтервальной интерполяции, а также способы их реализации в Mathcad.
Линейная интерполяция
Кусочно-линейная интерполяция является простейшим видом многоинтервальной интерполяции, при которой исходная функция на каждом частичном интервале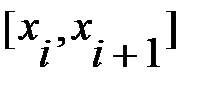 
аппроксимируется отрезком прямой, соединяющей точк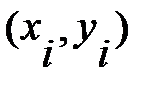и 
и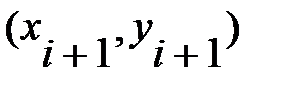 
.Запишем уравнение этой прямой.
Уравнение прямой на отрезке 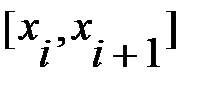имеет вид 
.
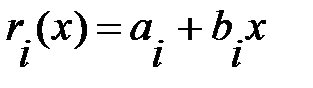Для определения коэффициентов a и b воспользуемся условиям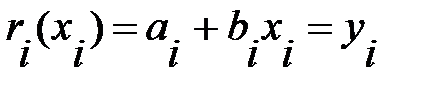и 
и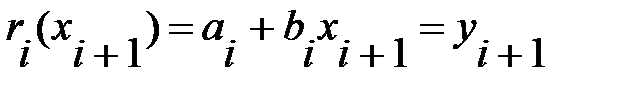 
. Решая эти уравнения, найдем коэффициенты 
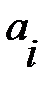и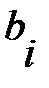 
.
, 
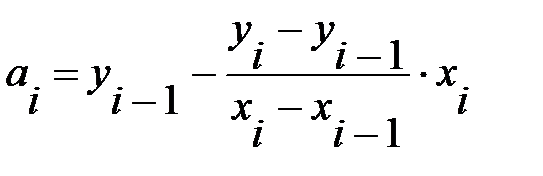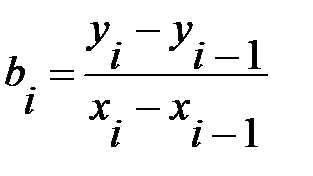
Таким образом, в случае линейной интерполяции интерполяционная функция на каждом из отрезков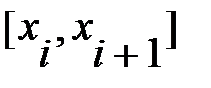 
определяется по формуле:
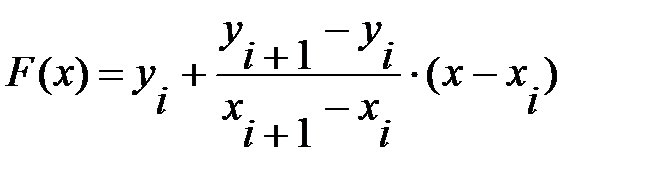
В Mathcad’е имеется встроенная функция linterp, осуществляющая линейную интерполяцию. Обращение к этой функции имеет вид linterp(vx,vy,x).
Аргументами этой функции являются два вектора vx и vy, содержащие координаты узлов интерполяции и независимая переменная х.
Рассмотрим пример построения линейной интерполяции в Mathcad.
Пример 5.2.
Для точек (1.1;7.7), (2.8;9.8), (3.7;6.3), (4.1;1.6) построить линейную интерполяцию. По полученной функции найти прогноз в точке x=3.5.
Решение:
1. Задаем координаты узлов интерполяции:
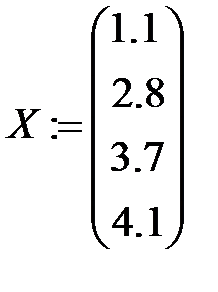
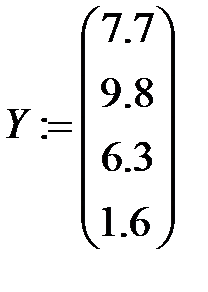
2. Определяем функцию li(x), осуществляющую линейную интерполяцию:
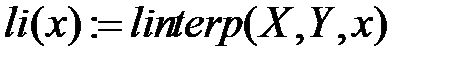
3. Строим график линейной интерполяционной функции:
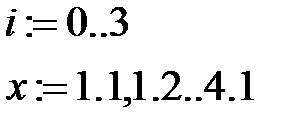
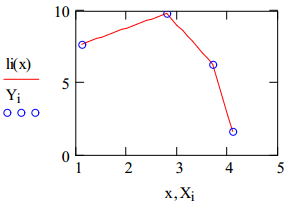
4. Находим прогноз в точке х=3.5
li(3.5)=7.078
Сплайн-интерполяция
Существенным недостатком линейной интерполяции является то, что в точках стыка разных интерполяционных полиномов оказывается разрывной их первая производная. Этот недостаток устраняется при использовании особого вида много интервальной интерполяции.
Интерполяции сплайнами (англ. spline – рейка, линейка).
Сплайн – это функция, которая на каждом частичном интервале представляется полиномом некоторой степени, а на всем заданном отрезке непрерывна вместе с несколькими своими производными. На практике широкое применение получили сплайны третьей степени (кубические сплайны).
На интервале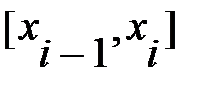 
кубический сплайн можно представить в виде:
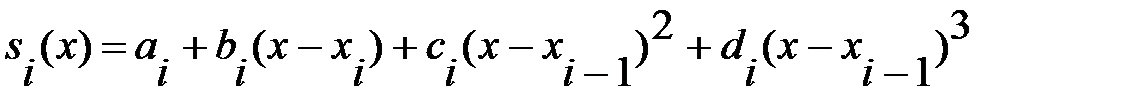, (5.5)
где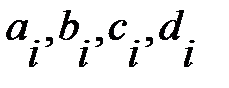 
- коэффициенты сплайнов;
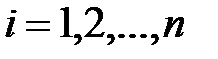- номер сплайна (интервала).
Коэффициенты сплайна определяются из следующих условий:
1) Условия Лагранжа:
, 
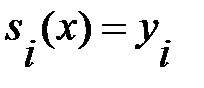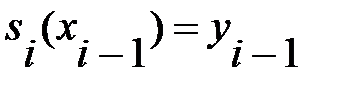(5.6)
2) Условия непрерывности первой и второй производных сплайнов в узлах:
, 
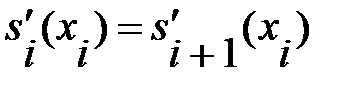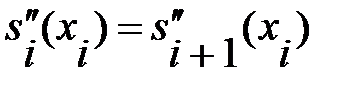(5.7)
Кроме этого необходимо задать дополнительные условия на концах интервала, т.е. в точках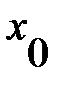 
и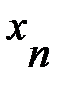 
. Если потребовать нулевой кривизны сплайна в этих точках, то дополнительными условиями будут являться равенства нулю вторых производных сплайнов на концах интервала интерполяции:
, 
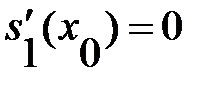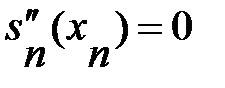(5.8)
Дополнительные условия могут быть и иными, их выбор зависит от конкретной задачи.
Подставив выражение (5.5) в условия (5.6), (5.7), (5.8), получим систему из 4n уравнений относительно коэффициентов сплайнов 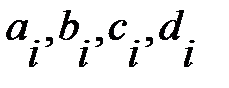. Решив эту систему, определим коэффициенты сплайна.
Интерполяция сплайнами имеет очень простую и наглядную физико-механическую аналогию. Если попытаться совместить упругую металлическую линейку с узловыми точками, то форма, которую примет в этом случае линейка будет совпадать с графиком кубического сплайна (сплошная линия на рис.1). Вне узловых точек, где линейка свободна, она описывается уравнением прямой. Соответствующее поведение сплайна обеспечивается условием (5.8).
Для кубической сплайн-интерполяции в Mathcad используется встроенная функция interp. Обращение к этой функции имеет вид:
interp(vs,X,Y,x)
Функция interp имеет следующие аргументы:
· vs – вектор вторых производных, созданный функцией lspline(X,Y), pspline(X,Y) или cspline(X,Y);
· X – вектор опытных значений аргумента, расположенных
в порядке возрастания;
· Y – вектор опытных значений функции;
· х – значение аргумента, при котором вычисляется интерполирующее значение.
Перед вызовом функции interp необходимо определить первый из ее аргументов – вектор vs. Делается это при помощи одной из трех встроенных функций тех же аргументов Х и Y:
· lspline(X,Y) – создает вектор коэффициентов кривой, которая приближается к прямой линии в граничных точках;
· pspline(X,Y) – создает вектор коэффициентов кривой, которая приближается к квадратичной параболе в граничных точках;
· сspline(X,Y) – создает вектор коэффициентов кривой, которая приближается к кубической параболе в граничных точках;
Выбор конкретной функции сплайн-коэффициентов влияет на интерполяцию вблизи конечных точек интервала.
Пример 5.3
Для точек (1.1;7.7), (2.8;9.8), (3.7;6.3), (4.1;1.6) построить кубическую сплайн-интерполяцию. По полученной функции найти прогноз в точке x=3.5.
Решение:
1. Определяем координаты узлов интерполяции:
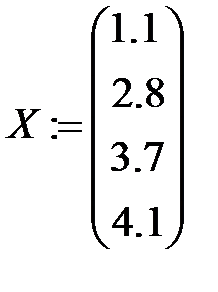
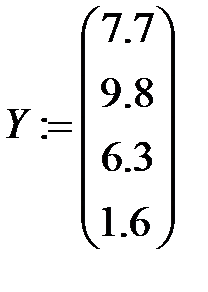
2. Определяем вектор коэффициентов сплайна:
vs := cspline(X, Y)
3. Строим график кубической сплайн интерполяции:
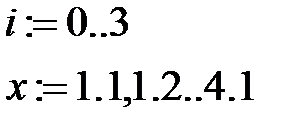
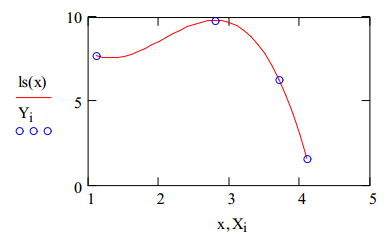
4. Находим прогноз в точке х=3.5
ls(3.5) = 7.81
Дата: 2019-02-18, просмотров: 1096.
