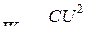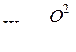При зарядке конденсатора между его обкладками появляется электрическое поле, энергия которого  или . При разрядке конденсатора на катушку индуктивности в ней возникает магнитное поле, энергия которого 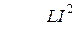. В идеальном контуре максимальная энергия электрического поля равна максимальной энергии магнитного поля:

.

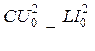Энергия заряженного конденсатора периодически изменяется со временем по закону

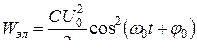
или

.

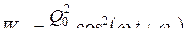Учитывая, что , получаем

.

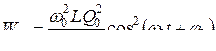Энергия магнитного поля соленоида изменяется со временем по закону

.

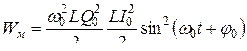Учитывая, что 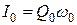, получаем

.

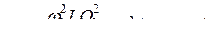Полная энергия электромагнитного поля колебательного контура равна

.

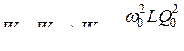Таким образом, в идеальном контуре суммарная энергия сохраняется, электромагнитные колебания незатухающие.

Вынужденные электромагнитные колебания.

Рассмотренные выше колебания происходили с частотами, определяемыми параметрами самой колебательной системы. Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Колебания, возникающие под действием внешней периодически изменяющейся ЭДС, называют вынужденными электромагнитными колебаниями.

Для того чтобы в колебательном контуре возникли вынужденные колебания, необходимо подвести к контуру внешнюю, периодически изменяющуюся по гармоническому закону, ЭДС или переменное напряжение

,

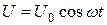где U₀ – максимальное значение напряжения, w – циклическая (круговая) частота.

Тогда аналогично вынужденным механическим колебаниям уравнение вынужденных электромагнитных колебаний имеет вид

.

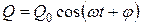В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими.

Амплитуда и фаза колебаний зависят от w и определяются следующими выражениями:

,

.

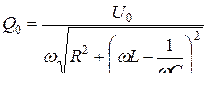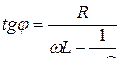Сила тока в контуре при установившихся колебаниях – это скорость изменения заряда, определяется по формуле:

.

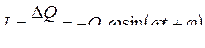Из сравнения формул Q, U и I следует, что колебания заряда (напряжения) и тока сдвинуты на p/2.

Электромагнитное поле

Согласно теории электромагнитного поля, переменное электрическое поле порождает переменное магнитное. Эти поля имеют вихревой характер: силовые линии порождающего поля концентрически охвачены силовыми линиями порождаемого поля. В результате образуется система «переплетенных» между собой электрических и магнитных полей.

Магнитное поле возникает вокруг проводников, по которым текут токи. Силовые линии магнитного поля всегда замкнуты, откуда следует, что электрические токи, порождающие магнитное поле, также должны быть замкнуты.

Если по проводнику протекает постоянный ток, т. е. ток проводимости, то линии тока замкнуты.

Рассмотрим случай, когда в электрическую цепь включен конденсатор. Между обкладками конденсатора заряды перемещаться не могут. Это приводит к тому, что линии тока обрываются у поверхности обкладок конденсатора, ток проводимости, текущий по проводнику, соединяющему обкладки конденсатора, оказывается разомкнутым. Если напряжение источника тока является переменным, то конденсатор попеременно заряжается и разряжается, в цепи идет ток. Это свидетельствует о том, что линии тока замкнуты. Между обкладками конденсатора изменяющийся электрический заряд создает переменное электрическое поле, которое Максвелл назвал током смещения.

Ток смещения – переменное электрическое поле, подобно току проводимости, порождает магнитное поле, силовые линии которого всегда замкнуты.

Таким образом, электрическое и магнитное поля взаимосвязаны: изменение одного из них порождает другое. Эти поля – проявление единого электромагнитного поля.

Электромагнитное поле – особая форма материи. Оно существует реально, т. е. независимо от нас, от наших знаний о нем. Неотъемлемой характеристикой материи является энергия. Под энергией электромагнитного поля подразумевается сумма энергий электрического и магнитного полей:

.

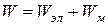Соответственно плотность энергии электромагнитного поля складывается из плотностей энергий электрического и магнитного полей:

.

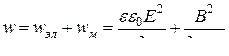Электромагнитные волны

В общем случае утверждать, что в данной точке пространства существует только электрическое или только магнитное поле, нельзя. Предположим, что какой-то заряд, покоящийся относительно Земли, создает неоднородное электрическое поле, магнитного поля вокруг заряда нет. Если наблюдатель находится в системе координат, движущейся относительно Земли, то неоднородное электрическое поле, созданное этим зарядом, для него уже переменно во времени. Это переменное электрическое поле порождает магнитное. Таким образом, для этого наблюдателя существуют одновременно и электрическое и магнитное поля.

Индукция 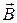 магнитного поля, возникающего в результате изменения электрического, пропорциональна скорости изменения напряженности электрического поля: 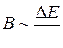. Напряженность  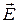электрического поля, возникающего в результате изменения магнитного поля, согласно закону Фарадея, пропорциональна скорости изменения индукции магнитного поля: .

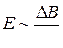Если в какой-либо точке пространства возбудить вихревое электрическое поле, то силовые линии возникающего переменного магнитного поля охватывают силовые линии электрического поля концентрическими окружностями. Меняющееся магнитное поле порождает электрическое поле, силовые линии которого охватывают силовые линии магнитного поля, и т.д.

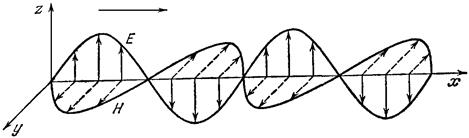
Значит, переменные электрическое и магнитное поля взаимосвязаны, они поддерживают друг друга и могут существовать независимо от источника, их породившего, распространяясь в пространстве в виде электромагнитной волны. Другими словами, электромагнитные волны – это распространяющееся в пространстве переменное электромагнитное поле.

Из теории Максвелла следует, что электромагнитные волны являются поперечными: векторы 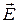 и 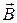 взаимно-перпендикулярны и лежат в плоскости, перпендикулярной вектору  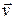– скорости распространения волны. Кроме того, в электромагнитной волне векторы  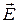и 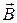 всегда колеблются в одинаковых фазах, одновременно достигают максимума, одновременно обращаются в нуль.

Таким образом, электромагнитная волна является волной поперечной.

Согласно теории Максвелла, скорость распространения электромагнитных волн – величина конечная. Она определяется электрическими и магнитными свойствами среды, в которой распространяется электромагнитная волна:

,

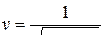где e₀ и m₀ – электрическая и магнитная постоянные; e и m – относительные диэлектрическая и магнитная проницаемости среды.

Если электромагнитная волна распространяется в вакууме, то e = 1, m = 1.

Вычислим скорость распространения электромагнитной волны в вакууме:

.

Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме: .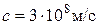

Расстояние, на которое перемещается электромагнитная волна за время, равное одному периоду колебания, называется длиной волны. Если v – скорость распространения электромагнитной волны в однородной среде, T – ее период, n – частота, l – длина, то 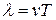или 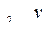. Для вакуума  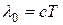или

.

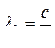Так как скорость волны зависит от e  и m  среды, то при переходе волны из одной среды в другую изменяются v и l, а частота колебаний остается прежней.

Если волна переходит из вакуума в среду с диэлектрической проницаемостью e и магнитной m, то длина волны уменьшается:

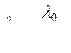
где l₀ – длина волны в вакууме.

Вопросы для самоконтроля:

1. Каким образом возникают свободные колебания в колебательном контуре?

2. От чего зависит период свободных колебания в контуре?

3. Какие колебания называются затухающими?

4. Какие электромагнитные колебания называют вынужденными?

5. Чему равна плотность энергии электромагнитного поля?

6. Что представляет собой электромагнитная волна?

7. От чего зависит скорость распространения электромагнитной волны?

8. Что называют длиной электромагнитной волны?