Цель: познакомиться с условиями возникновения механических колебаний и волн, их характеристиками и видами.
Основные понятия:
Механические колебания – движения, которые точно или приблизительно повторяются через определенный интервал времени.
Свободные колебания – колебания, которые происходят в системе под действием внутренних сил, после того как система была выведена из состояния равновесия.
Вынужденные колебания – колебания, которые происходят под действием внешней, периодически изменяющейся силы.
Гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.
Амплитуда колебаний – максимальное значение колеблющейся величины.
Период колебаний – время, за которое совершается одно полное колебание.
Частота колебаний – число полных колебаний, совершаемых за единицу времени.
Затухающие колебания – колебания, амплитуда которых с течением времени уменьшается.
Логарифмический декремент затухания – физическая величина, обратная числу колебаний, по истечении которых амплитуда убывает в е раз.
Время релаксации – промежуток времени, в течение которого амплитуда убывает в е раз.
Резонанс – явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты колебаний с частотой собственных колебаний системы.
Упругая волна – процесс распространения возмущения в упругой среде.
Продольные волны – волны, в которых частицы колеблются около положений равновесия вдоль направления распространения волны.
Поперечные волны – волны, в которых частицы колеблются около положений равновесия поперек направлению распространения волны.
Длина волны – расстояние, на которое распространяется волна за время, равное периоду колебаний.
Фазовая скорость волны – скорость, с которой распространяется определенное значение фазы волны.
Волновая поверхность (волновой фронт) – поверхность, каждая точка которой в некоторый фиксированный момент времени имеет одинаковую фазу.
Механические колебания
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Таким свойством повторяемости обладают, например, качания маятника часов, колебания струны или ножек камертона, напряжение между обкладками конденсатора в контуре радиоприемника и т. п.
В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т. д. Мы будем рассматривать механические колебания.
В зависимости от характера воздействия, оказываемого на колеблющуюся систему, различают свободные (или собственные) колебания и вынужденные колебания.
Свободными или собственными называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок, либо она была выведена из положения равновесия. Примером могут служить колебания шарика, подвешенного на нити (маятник). Для того чтобы вызвать колебания, можно либо толкнуть шарик, либо, отведя в сторону, отпустить его.
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Примером могут служить колебания моста, возникающие при прохождении по нему людей, шагающих в ногу.
Простейшими являются гармонические колебания, т. е. такие колебания, при которых колеблющаяся величина (например, отклонение маятника) изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническим, и, во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.
Рассмотрим колебания, происходящие под действием упругой силы, например колебания пружинного маятника. Пружинный маятник состоит из массивного шара, насаженного на горизонтальный стержень, вдоль которого он может скользить. На стержень надета стальная пружина, закрепленная на его конце и на шаре. Массой пружины по сравнению с массой шара можно пренебречь. Определим положение шара его смещением х из положения равновесия; в  положении равновесия х = 0 (точка О на рис. а). Если его передвинуть в положение В (рис. б), сжав пружину, а затем отпустить, то он начнет ускоренно двигаться влево под действием упругой силы пружины
положении равновесия х = 0 (точка О на рис. а). Если его передвинуть в положение В (рис. б), сжав пружину, а затем отпустить, то он начнет ускоренно двигаться влево под действием упругой силы пружины 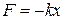 . Знак минус означает, что сила направлена в сторону, противоположную смещению х. Коэффициент k положителен. По второму закону Ньютона:
. Знак минус означает, что сила направлена в сторону, противоположную смещению х. Коэффициент k положителен. По второму закону Ньютона:
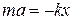 .
.
Решение данного уравнения имеет вид:
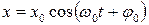 ,
,
где 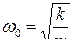 .
.
Данное выражение определяет гармонические колебания.
Величину x 0, равную максимальному смещению шара из положения равновесия, называют амплитудой колебаний. Выражение 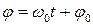 , стоящее под знаком косинуса, определяет смещение х в данный момент времени t. Его называют фазой колебания. В момент начала отсчета времени (t = 0) фаза колебания равна j 0. Поэтому величину j 0 называют начальной фазой колебания. Фазу измеряют в радианах.
, стоящее под знаком косинуса, определяет смещение х в данный момент времени t. Его называют фазой колебания. В момент начала отсчета времени (t = 0) фаза колебания равна j 0. Поэтому величину j 0 называют начальной фазой колебания. Фазу измеряют в радианах.
Величину w 0, входящую в выражение для фазы колебания, называют циклической (или круговой) частотой колебаний. Физический смысл циклической частоты связан с понятиями периода колебаний Т и частоты колебаний n. Периодом незатухающих колебаний называют тот наименьший промежуток времени Т, по истечении которого повторяются значения всех физических величин, характеризующих колебания. За время Т совершается одно полное колебание.
Колебания шара характеризуются не только его смещением, но также скоростью v и ускорением а. Шар движется прямолинейно вдоль оси О x. Поэтому значения скорости v и ускорения а шара на положительное направление оси О x можно получить, из уравнения гармонических колебаний:
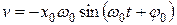 ,
,
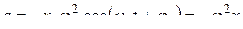 .
.
Графики зависимости х, v и а от времени t показаны на рисунке,  где введены обозначения
где введены обозначения 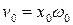 ,
,  .
.
Из определения периода колебаний Т следует, что за время Т фаза колебаний изменяется на 2p рад. В самом деле, это наименьшее изменение фазы, при котором одновременно повторяются значения х, v и а. Следовательно,
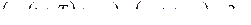
или
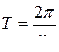 .
.
Частотой колебаний называют число полных колебаний, совершаемых за единицу времени:
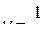 .
.
Тогда
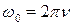 ,
,
т. е., циклическая частота w 0 численно равна числу полных колебаний, совершаемых за 2p с. В этом и состоит ее физический смысл.
Приведем еще пример колебательной системы.
Математическим маятником называют материальную точку, подвешенную на невесомой, нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести. На практике математическим маятником можно считать тяжелое тело, подвешенное на легкой нити, длина которой во много раз больше размеров тела. Период Т колебаний математического маятника можно определить по формуле
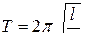 ,
,
где l –длина маятника.
Дата: 2019-02-25, просмотров: 381.