Ток проводимости в замкнутой цепи может возникнуть только под действием стороннего электрического поля. Следовательно, в замкнутом контуре, находящемся в переменном магнитном поле, появляется так называемое индуктированное электрическое поле. Энергетической мерой этого поля служит электродвижущая сила электромагнитной индукции Ei.
Дальнейшие исследования индукционного тока в контурах различной формы и размеров показали, что ЭДС электромагнитной индукции Ei в контуре пропорциональна скорости изменения магнитного потока F сквозь поверхность, натянутую на этот контур (закон Фарадея):
Ei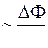 
.
Профессор Петербургского университета Ленц исследовал связь между направлением индукционного тока и характером вызвавшего его изменения магнитного потока. Он установил следующее правило (правило Ленца): при всяком изменении магнитного потока сквозь поверхность, натянутую на замкнутый контур, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.
Интересной иллюстрацией закона Ленца служит следующий опыт. На вертикальный железный сердечник катушки с большим числом витков провода свободно надето алюминиевое кольцо А. Катушку можно включить в цепь аккумуляторной батареи Б с помощью ключа К. При замыкании цепи катушки кольцо подскакивает вверх и падает на стол рядом с ней. Чтобы вновь надеть это кольцо на сердечник катушки, находящейся под током, требуется приложить некоторое усилие. В момент выключения тока кольцо, надетое на сердечник, прижимается к катушке. Такое поведение кольца объясняется возникновением в нем индукционного тока. Если ток в катушке отсутствует, то магнитный поток сквозь поверхность, ограниченную кольцом (магнитный поток, сцепленный с кольцом), равен нулю. При замыкании цепи катушки магнитный поток, сцепленный с кольцом, резко возрастает. В кольце возникает индукционный ток, магнитное поле которого, согласно закону Ленца, должно быть противоположно по направлению магнитному полю тока в катушке. Поэтому индукционный ток в кольце направлен противоположно току в витках катушки. Между такими токами действует сила взаимного отталкивания, и кольцо подбрасывается вверх. При размыкании цепи катушки магнитный поток, сцепленный с кольцом, быстро уменьшается. Теперь в кольце возникает индукционный ток, совпадающий по направлению с током в катушке. Поэтому кольцо притягивается к ней.
Направления индукционного тока Ii при увеличении и уменьшении магнитного потока, сцепленного с кольцом, показаны на рисунке.
Условимся считать ЭДС электромагнитной индукции в контуре положительной, если магнитный момент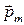 
соответствующего ей индукционного тока образует острый угол с линиями магнитной индукции того поля, которое наводит этот ток. Тогда в случае, изображенном на рисунке а, Ei < 0, а в случае показанном на рисунке б, Ei > 0.
Объединяя закон Фарадея и правило Ленца, получим формулу
Ei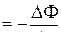 
,
являющуюся математическим выражением основного закона электромагнитной индукции: электродвижущая сила электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, натянутую на контур.
Самоиндукция. Индуктивность
Электрический ток I, текущий в любом контуре, создает пронизывающий этот контур магнитный поток Ф. При изменениях I будет изменяться также Ф и, следовательно, в контуре будет индуцироваться ЭДС. Это явление называется самоиндукцией. Магнитная индукция В пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток в контуре I и создаваемый им полный магнитный поток через контур Ф друг другу пропорциональны:
Ф = L I.
Коэффициент пропорциональности L между силой тока и полным магнитным потоком называется индуктивностью контура.
Линейная зависимость Ф от I имеет место лишь в том случае, если среда, которой окружен контур, не является ферромагнетиком.
Из сказанного следует, что индуктивность L зависит от геометрии контура (т. е. его формы и размеров) и от магнитных свойств (от m) окружающей контур среды. Например, для соленоида длиной l и площадью сечения витка S, находящегося в вакууме или воздухе,
,
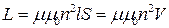где m0 – магнитная постоянная, n – число витков, приходящихся на единицу длины, V = l S – объем соленоида. Заменив n через N/l (N – общее число витков соленоида) получим
.
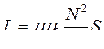За единицу индуктивности в СИ принимается индуктивность такого проводника, у которого при силе тока в нем в 1 А возникает полный поток Ф, равный 1 Вб. Эту единицу называют генри (Гн).
Как следует из опытов, индуктивность всякого контура зависит от свойств среды, в которой он находится. Например, если в катушку поместить железный сердечник, то сила тока самоиндукции возрастет во много раз. Это свидетельствует о том, что увеличилась индуктивность катушки.
Величину, равную отношению индуктивности L контура в однородной среде к индуктивности L0 контура в вакууме, называют магнитной проницаемостью среды:
.
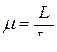Магнитная проницаемость, характеризующая магнитные свойства вещества, – величина безразмерная.
При изменениях силы тока в контуре возникает ЭДС самоиндукции Es , равная
Es .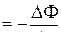
Если L при изменениях силы тока остается постоянной (что, как уже отмечалось, возможно лишь при отсутствии ферромагнетиков), выражение для Es имеет вид
Es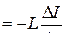 
.
Данное соотношение дает возможность определить индуктивность L как коэффициент пропорциональности между скоростью изменения силы тока в контуре и возникающей вследствие этого ЭДС самоиндукции. Однако такое определение правильно лишь в случае, когда L = const. В этом случае изменение силы тока со скоростью 1 А/сек в проводнике с L = 1 Гн приводит к возникновению Es = 1 В.
Примером, иллюстрирующим явление самоиндукции, является ток при замыкании и размыкании цепи.
По правилу Ленца дополнительные токи, возникающие в проводниках вследствие самоиндукции, всегда направлены так, чтобы воспрепятствовать изменениям тока, текущего в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при размыкании цепи происходит не мгновенно, а постепенно.
После отключения источника ЭДС сила тока в цепи не обращается мгновенно в нуль, а убывает по экспоненциальному закону и чем больше отношение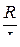 
, т. е. чем больше сопротивление цепи и меньше ее индуктивность, тем быстрее происходит убывание тока.
При включении источника ЭДС сила тока в цепи не возрастает мгновенно до установившегося значения, а растет по экспоненциальному закону и чем больше отношение 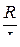, т. е. чем больше сопротивление цепи и меньше ее индуктивность, тем круче происходит нарастание тока.
Из сказанного следует важный практический вывод: контур, содержащий индуктивность, нельзя резко размыкать. Если он рассчитан на рабочее напряжение E, то при резком размыкании возникающие в нем большие Es могут привести к пробою изоляции и порче электроприборов. Сопротивление в такой контур надо вводить постепенно, с тем, чтобы Es не превысила дозволенных значений. Опасным может быть и резкое включение E, что может вызвать на отдельных участках контура недопустимо большие Es.
Взаимная индукция
Рассмотрим систему, состоящую из двух контуров 1 и 2, расположенных друг относительно друга не очень далеко. Если в первом контуре течет ток силы I1, он создает через другой контур пропорциональный I1 поток
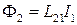
(поле, создающее этот поток, изображено на рисунке сплошными линиями).
При изменениях тока I1 во втором контуре индуцируется ЭДС
Ei 2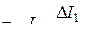 
Аналогично, при протекании во втором контуре тока силы I2 возникает связанный с первым контуром поток
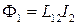
(поле, создающее этот поток, изображено пунктирными линиями).
При изменениях тока I2 в контуре 1 индуцируется ЭДС
Ei 1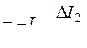 
Контуры 1 и 2 называются связанными, а явление возникновения ЭДС в одном из контуров при изменениях силы тока в другом называется взаимной индукцией.
Коэффициенты пропорциональности L12 и L21 называются взаимной индуктивностью (или коэффициентом взаимной индукции) контуров.
Эти коэффициенты всегда равны друг другу:
L12 = L21.
Взаимная индуктивность L12 зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости, окружающей контуры среды. Измеряется L12 в тех же единицах, что и индуктивность L.
На явлении взаимной индукции основано действие трансформатора – устройства, предназначенного для преобразования напряжения и силы переменного тока.
Энергия магнитного поля
Рассмотрим цепь, изображенную на рисунке. Сначала замкнем соленоид L на батарею E ; в нем установится ток I, который обусловит магнитное поле, сцепленное с витками соленоида. Если, отключив соленоид от батареи, замкнуть его через сопротивление R, то в образовавшейся цепи будет некоторое время течь постепенно убывающий ток, подчиняющийся закону Ома для полной цепи
I = Es /R
где Es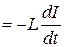 
– ЭДС самоиндукции (предполагаем, что проводники с током находятся в неферромагнитной однородной и изотропной среде, сопротивлением соленоида пренебрегаем).
Таким образом
Es = IR .
Умножим обе части данного выражения на I D t:
Es I D t = I2R D t .
Правая часть равенства представляет собой количество теплоты, выделяемое в проводнике при протекании в нем тока.
Левая часть данного равенства представляет собой элементарную работу, совершаемую током за время D t, обусловленную индукционными явлениями. Полная работа, совершаемая в цепи за все время, в течение которого происходит исчезновение магнитного поля, равная сумме элементарных работ, есть:
.
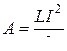Данная работа идет на приращение внутренней энергии проводников, т. е. на их нагревание. Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в окружающем соленоид пространстве. Поскольку никаких других изменений в окружающих электрическую цепь телах не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается данная работа. Таким образом, мы приходим к выводу, что проводник с индуктивностью L, по которому течет ток I, обладает энергией
,
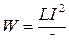которая локализована в возбуждаемом током магнитном поле.
Выразим энергию магнитного поля через величины, характеризующие само поле. В случае бесконечного соленоида
, 
,
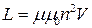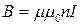откуда
.
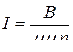Подставляя эти значения L и I в выражение для энергии и производя преобразования, получим
.
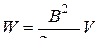Магнитное поле бесконечно длинного соленоида однородно и отлично от нуля только внутри соленоида. Следовательно, энергия заключена в пределах соленоида и распределена по его объему с постоянной плотностью w, которую можно получить, разделив W на V. Произведя это деление, получим
.
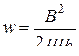Полученное выражение для плотности энергии магнитного поля имеет вид, аналогичный выражению для плотности энергии электрического поля, с тем лишь отличием, что электрические величины в нем заменены соответствующими магнитными.
Вопросы для самоконтроля:
1. В чем состоит явление электромагнитной индукции? Опишите опыты Фарадея.
2. Что называется магнитным потоком?
3. Сформулируйте закон Фарадея и правило Ленца для электромагнитной индукции. Проиллюстрируйте их примерами.
4. Как определяется направление индукционного тока?
5. Сформулируйте основной закон электромагнитной индукции.
6. В чем состоит явление самоиндукции?
7. Что называется индуктивностью проводящего контура?
8. От чего зависят индуктивность проводящего контура и каков ее физический смысл?
9. Напишите выражение для ЭДС самоиндукции.
10. В чем состоит явление взаимной индукции?
12. Напишите выражения для ЭДС взаимной индукции.
13. Что называется взаимной индуктивностью двух контуров? От чего она зависит и каков ее физический смысл?
14. Приведите выражение для объемной плотности энергии магнитного поля.
15. Как распределена энергия магнитного поля соленоида в пространстве?
Дата: 2019-02-25, просмотров: 382.
