На практике всякое колебание, которое не поддерживается извне, затухает, амплитуда его колебания с течением времени уменьшается. Причина затухания обуславливается силами, тормозящими движение, например, силой трения в месте подвеса при колебании маятника или силой сопротивления среды. Чтобы исследовать этот вопрос, надо написать уравнение, выражающее второй закон Ньютона, принимая в расчет силы сопротивления. Мы ограничимся рассмотрением случая, когда точка совершает прямолинейное колебание в вязкой среде. Сила сопротивления среды зависит от скорости движения точки и в случае малых скоростей ее можно считать пропорциональной скорости v; направлена она в сторону, противоположную скорости; таким образом, силу сопротивления можно положить равной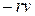 
, где r – постоянная величина, называемая коэффициентом сопротивления. Эта сила прибавится к упругой силе –kx, откуда полная сила, действующая на точку, равна 
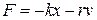и, следовательно, второй закон Ньютона может быть написан в виде:
.
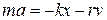Решение последнего уравнения имеет вид
,
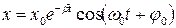где введены обозначения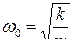 
и 
.
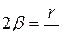Это решение представляет собою колебание с амплитудой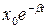 
, уменьшающейся с течением времени. Период колебания 
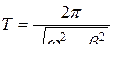в среде с сопротивлением больше, чем период колебания 
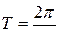такой же массы m под действием такой же упругой силы 
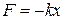в среде без сопротивления. График зависимости х от времени представлен на рисунке. Как видно, колебания затухают со временем.
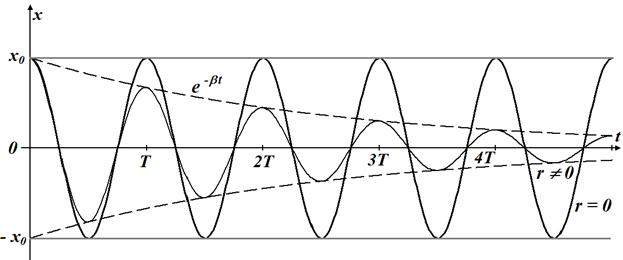
Логарифм отношения двух последовательных значений амплитуд, отстоящих друг от друга на время, равное периоду Т, называется логарифмическим декрементом затухания
.
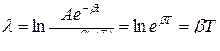Поясним физический смысл величин l и b. Обозначим через t промежуток времени, за который амплитуда колебаний уменьшается в e paз. Тогда
,
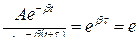откуда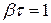 
, или
.
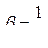Следовательно, коэффициент затухания b есть физическая величина, обратная промежутку времени t, в течение которого амплитуда убывает в е раз. Величину t называют временем релаксации. Пусть, например, b= 102с-1 – это означает, что амплитуда колебаний убывает в е раз за 10-2 с. Пусть N – число колебаний, после которых амплитуда уменьшается в е раз. Тогда
,
.
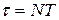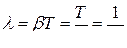Следовательно, логарифмический декремент затухания l есть физическая величина, обратная числу колебаний N, по истечении которых амплитуда убывает в е раз. Пусть, например, l = 0,01. Это значит, что амплитуда колебаний убывает в е раз по истечении 100 колебаний.
Вынужденные колебания
Рассмотренные ранее колебания происходили с собственной частотой w 0, определяемой параметрами самой колебательной системы. Чтобы в реальной колебательной системе получить незатухающие колебания, необходимо компенсировать потери энергии.
Колебания, возникающие под действием внешней периодически изменяющейся силы, называют вынужденными колебаниями. За счет внешней силы периодически компенсируются потери энергии системы. Характер вынужденных колебаний определяется как внешней силой, так и свойствами самой системы. По прошествии некоторого промежутка времени в системе устанавливаются вынужденные колебания с частотой, равной частоте внешней силы.
Пусть вынужденные колебания возникают под действием внешней периодически изменяющейся силы
,
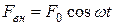где F0 – амплитуда вынуждающей силы, w – циклическая частота.
Определим амплитуду вынужденных колебаний, считая, что затухание отсутствует. В этом случае на тело массой m действуют сила Fвн и квазиупругая сила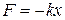 
.
В соответствии со вторым законом Ньютона:
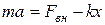
учитывая, что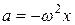 
, а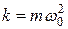 
, получим
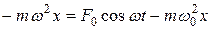
откуда
,
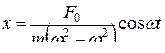где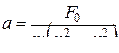 
– амплитуда вынужденных колебаний.
Анализируя выражение для амплитуды, можно сделать вывод, что чем меньше разность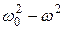 
, тем больше амплитуда вынужденных колебаний.
С приближением частоты вынуждающей силы к частоте собственных колебаний колебательной системы амплитуда вынужденных колебаний резко возрастает. В идеальных колебательных системах (отсутствуют силы сопротивления и трения) амплитуда вынужденных колебаний при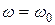 
максимальна и стремится к бесконечности. Реальные колебательные системы характеризуются коэффициентом затухания b; в них амплитуда конечна и достигает наибольшего значения при частоте, несколько меньшей w 0.
Резонанс – явление резкого возрастания амплитуды вынужденных колебаний, когда частота колебаний приближается к частоте собственных колебаний системы.
На рисунке приведены резонансные кривые для различных коэффициентов затухания, откуда видно, что с увеличением коэффициента затухания кривые становятся более пологими.
Явление механического резонанса впервые было описано Г. Галилеем. Механический резонанс может быть как полезным, так и вредным. Явление резонанса используется в вибромашинах, работающих в горнодобывающей области, в электро- и радиотехнике. Вредное действие резонанса связано с разрушениями, которые он может вызвать. Чтобы предотвратить нежелательные последствия резонанса, необходимо при конструировании различных сооружений и машин учитывать даже небольшие периодически действующие силы и вибрации или использовать успокоители колебаний, основанные на явлении антирезонанса.
Упругие волны
Упругой волной называют процесс распространения возмущения в упругой среде. При этом происходит распространение именно возмущения частиц среды, но сами частицы испытывают движения около своих положений равновесия. Среду при этом рассматривают как сплошную и непрерывную, отвлекаясь от ее атомистического строения.
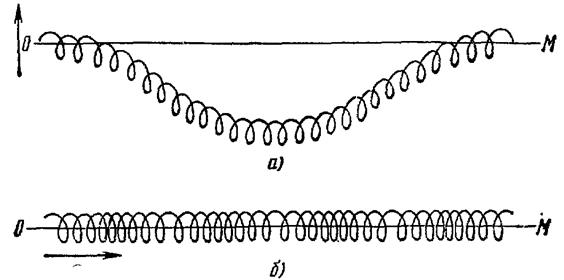
Различают волны продольные и поперечные, в зависимости от того, движутся ли частицы около своих положений равновесия вдоль или поперек направления распространения волны. На рис. а изображен случай, когда мы заставляем крайний виток длинной проволочной спирали, все витки которой упруго связаны друг с другом, колебаться в направлении, перпендикулярном к ОМ. В этом случае и для всех последующих витков направление колебаний будет перпендикулярным к направлению их распространения. Это пример поперечных волн. На рис. б изображен иной случай, когда направление колебаний параллельно направлению распространения. Это пример продольных волн.
Несмотря на большое разнообразие физических процессов, вызывающих волны, их образование происходит по общему принципу. Возмущение, происходящее в какой-нибудь точке среды в некоторый момент времени, проявляется спустя определенное время на интересующем нас расстоянии от первоначальной точки, т. е. передается с определенной скоростью.
Рассмотрим распространение возмущения вдоль оси Ox в положительном направлении без затухания (амплитуды колебаний всех точек одинаковы и равны А). Зададим колебание точки с x=0 (источник колебаний) уравнением
.
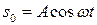До точки с некоторой произвольной координатой x возмущение от начала координат дойдет через время t, поэтому колебания этой точки запаздывают и описываются выражением
.
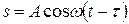Так как время и скорость распространения волны связаны зависимостью 
, то получим
,
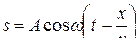где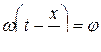 
- фаза волны.
Последнее уравнение является уравнением гармонической волны. Эта волна периодична во времени и пространстве, поскольку сама функция периодична и ее период равен 2 p. Из периодичности во времени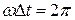 
находим 
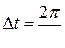. Этот промежуток времени называют периодом колебаний:
.
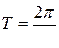Из периодичности в пространстве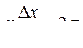 
находим 
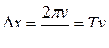. Расстояние D x называют длиной волны l. Таким образом, длина волны – это расстояние между ближайшими точками среды, колеблющимися с разностью фаз 2 p. Другими словами, это расстояние, на которое распространяется волна за время, равное периоду колебаний T:
.
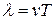Поскольку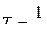 
, где n - частота колебаний, формулу для длины волны можно представить в виде:
.
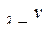Уравнение гармонической волны принято записывать в симметричном более удобном и простом виде. Для этого внесем w в скобку:
,
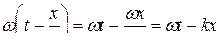где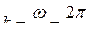 
, или
.
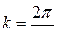Величину к называют волновым числом.
Тогда уравнение гармонической волны примет следующий симметричный вид:
.
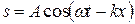Отметим, что фигурирующая выше скорость v – это фазовая скорость волны, т. е. скорость, с которой распространяется определенное значение фазы волны. Именно фаза характеризует определенное состояние движения частиц среды при прохождении волны.
Если волна распространяется не вдоль оси Ox, а в произвольном направлении, то уравнение для такой волны имеет вид:
,
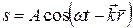причем направление распространения волны определяется волновым вектором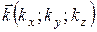 
, а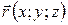 
- радиус- вектор, причем 
.
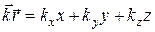Определим форму волновых поверхностей – поверхностей, каждая точка которой в некоторый фиксированный момент времени имеет одинаковую фазу (и, следовательно, одинаковое смещение). Рассмотрим фазу волны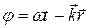 
в некоторый момент времени 
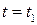. Фаза в данный момент времени должна быть некоторой постоянной величиной для некоторой совокупности точек:
,
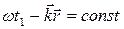или
,
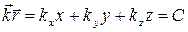где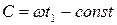 
- некоторая новая постоянная величина.
Уравнение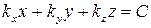 
определяет плоскость, перпендикулярную вектору 
.
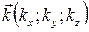Если волна распространяется вдоль оси Ox, то уравнение ее фазовой поверхности имеет вид:
.
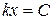Оно определяет плоскость, перпендикулярную вектору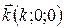 
(перпендикулярную оси Ox).
Таким образом, гармонические волны являются плоскими волнами. В плоской волне волновые поверхности имеют вид плоскостей. Когда говорят, что плоская волна распространяется вдоль оси Ox, то это надо понимать так, что ее волновые поверхности (плоскости) перпендикулярны этой оси.
Рассмотренные выше волны, распространяющиеся вдоль одной прямой, являются частным случаем волн. В упругой среде возможны волны иного вида, например, сферические волны.
В сферической волне амплитуда убывает обратно пропорционально расстоянию r от источника колебаний. Зависимость смещения от координат и времени имеет вид:
.
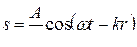Поверхность равных фаз в некоторый момент времени определяется уравнением r = const, т. е. представляет собой сферу радиуса r.
Отсюда и происходит название «сферическая» для такой волны.
Вопросы для самоконтроля:
1. Какое движение называют колебательным?
2. Какие колебания называют гармоническими?
3. Какие колебания называют свободными?
4. Дайте определения периода, частоты и амплитуды колебательного движения?
5. По какому закону изменяется скорость, ускорение при свободных гармонических колебаниях?
6. Какие механические колебания называют свободными?
7. От чего зависит период колебания математического, пружинного маятника?
8. От чего зависит полная энергия колеблющегося тела?
9. Какие механические колебания называются затухающими?
10. От чего зависит амплитуда, период затухающих колебаний?
11. Какие механические колебания называют вынужденными?
12. От чего зависит амплитуда вынужденных колебаний?
13. Какое явление называют механическим резонансом?
14. Что такое волновой процесс?
15. Что называется поперечной волной?
16. Что называется продольной волной?
17. Назовите характеристики волны. Какова связь между ними?
18. Запишите уравнение гармонической волны
Дата: 2019-02-25, просмотров: 302.
