Электромагнитными колебаниями называют периодические взаимосвязанные изменения зарядов, токов, напряженности электрического поля и индукции магнитного поля.

Простейшей идеализированной колебательной системой в механике являются, например, математический или пружинный маятник. Как было показано, в этих системах возникают свободные гармонические колебания. При механических колебаниях происходит периодическое превращение энергии системы из кинетической в потенциальную.

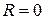Аналогичные процессы протекают при возникновении электромагнитных колебаний в системе, называемой колебательным контуром. Колебательный контур представляет собой электрическую цепь, состоящую из конденсатора С и индуктивности L, соединенных между собой. Если сопротивление контура , то такой колебательный контур называют идеальным.  

Рассмотрим возникновение свободных электромагнитных колебаний в идеальном колебательном контуре, пользуясь аналогией между механическими и электромагнитными явлениями. Чтобы возбудить колебания в контуре, необходимо: 1) либо сообщить конденсатору С некоторый заряд, в результате чего он будет обладать энергией 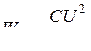; 2) либо возбудить в катушке индуктивности L ток, в результате чего она будет обладать энергией .

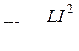Сообщим конденсатору заряд. В начальный момент времени (t = 0) заряд на обкладках конденсатора равен 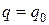 и ток в цепи отсутствует ( 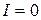). Между обкладками конденсатора появилось электрическое поле, энергия которого

,

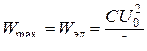где С – электроемкость конденсатора, U₀ – максимальное напряжение между обкладками конденсатора. Такое состояние колебательного контура аналогично состоянию математического маятника, отклоненного от положения равновесия на малый угол (рис. а).

Замкнем конденсатор С на индуктивность L. Конденсатор начнет разряжаться, при этом в контуре возникает электрический ток, вследствие чего в катушке индуктивности появляется магнитное поле 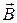. В идеальном контуре через четверть периода энергия электрического поля переходит в энергию магнитного поля:

,

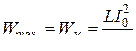где L – индуктивность, I₀ – максимальный ток, протекающий через катушку. Напряжение между обкладками конденсатора при этом равно нулю: 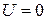, 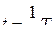. Такое состояние колебательного контура аналогично состоянию математического маятника при прохождении положения равновесия, т. е. когда потенциальная энергия системы полностью превращается в кинетическую энергию (рис. б).

После этого магнитное поле должно быстро уменьшаться до нуля, так как нет токов, его поддерживающих. Изменяющееся магнитное поле вызывает ток самоиндукции в катушке индуктивности, который, согласно закону Ленца, поддерживает убывающий ток разрядки конденсатора. Таким образом, ток, продолжая течь в том же направлении, перезаряжает конденсатор. Когда закончится перезарядка конденсатора, ток в контуре будет равен нулю. Следовательно, через время, равное половине периода ( 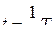), магнитное поле исчезнет, т.е. энергия магнитного поля полностью превратится в энергию электрического поля (рис. в). Это состояние колебательного контура аналогично состоянию математического маятника, отклоненного от положения равновесия на такой же малый угол, но уже в сторону, противоположную состоянию, показанному на рис. а.

После этого конденсатор снова начинает разряжаться, в контуре возникает ток, но уже противоположного направления. Через время 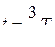 конденсатор разрядится полностью, энергия электрического поля вновь превратится в энергию магнитного поля (рис. г).

Через время 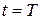 состояние контура станет таким же, как и в начальный момент времени (рис. д). Затем весь процесс повторяется.

В контуре возникают колебания, при которых изменяются напряжение между обкладками конденсатора и сила тока. При этом происходит превращение энергии электрического поля в энергию магнитного поля и наоборот, т. е. возникают электромагнитные колебания. Если сопротивление контура равно нулю, то процесс превращения энергии электрического поля в энергию магнитного поля должен продолжаться бесконечно, возникают незатухающие электромагнитные колебания. Эти колебания называют собственными, или свободными, так как они происходят без воздействия внешней вынуждающей силы.

Период незатухающих собственных колебаний, возникающих в колебательном контуре, определяется по формуле

,

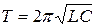которую называют формулой Томсона.

Циклическая, или круговая, частота собственных электромагнитных колебаний

.

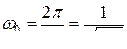В идеальном колебательном контуре колебания заряда происходят по закону

,

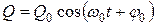где Q₀ – максимальный заряд на обкладках конденсатора, j₀ – начальная фаза.

Периодическое изменение заряда на обкладках конденсатора вызывает переменную разность потенциалов – переменное напряжение U и переменный электрический ток

,

где 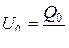– амплитуда напряжения.

Учитывая, что электрический ток характеризует скорость изменения заряда на обкладках конденсатора, можно записать

,

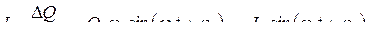где 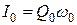– амплитуда тока.

Таким образом, по гармоническому закону изменяется не только заряд на обкладках конденсатора, но и напряжение и сила тока в контуре, т.е. возникают свободные электромагнитные колебания.

Из выражений для Q, U и I вытекает, что колебания заряда (напряжения) и тока в контуре сдвинуты по фазе на p/2. Следовательно, ток достигает максимального значения в те моменты времени, когда заряд (напряжение) на обкладках конденсатора равен нулю, и наоборот.