При решении задач на квадратичную функцию большое практическое значение имеет наличие соответствия между алгебраическим описанием задачи и ее геометрической интерпретацией – изображением на координатной плоскости эскиза графика функции. Именно благодаря этой
особенности у нас всегда есть возможность проверить правильность и непротиворечивость своих теоретических рассуждений.
Квадратичная функция является одной из главных функций школьной математики, для которой построена полная теория и доказаны все свойства. Учащиеся должны четко понимать и знать все эти свойства. При этом задач на квадратичную функцию существует великое множество - от очень простых, которые вытекают непосредственно из теории и формул, до самых сложных, решение которых требует анализа и глубокого понимания всех свойств функции.
Квадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами. Первой рассматривается функция у=х2.
Графиком квадратичной функции является парабола, которая для функции имеет вид:

Рис.1. График функции у=х2, построенный в среде GeoGebra.
1Свойства графика функции у=х2:
· Область определения функции – множество всех действительных чисел D(y)=R;
· Область значений функции E(y)= [0; +∞);
1 Алгебра. 9 класс: учеб.для шк, и кл. с углубл, изуч, тематики/Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков. – 5-е изд. – М.: Мнемозина, 20006. – 439 с. : ил.
· Функция четная;
· y=0 при x=0, y>0 при x>0 и приx<0
· Функция возрастает на промежутке [0; +∞) и убывает на промежутке (-∞;0]. Функция имеет наименьшее значение y=0 при x=0.
Вершина параболы у=х2 – точка (0;0), а ось симметрии параболы – ось Oy. Ветви параболы направлены вверх.
График функции y=kf(x) при получается из графика функции y=f(x) растяжением от оси Ox в k раз, а при 0<k <1 –сжатием к оси Ox в 1 𝑘 раз. Следовательно, график функции y=2𝑥2есть парабола, полученная из графика функции у=х2 растяжением от оси Ox в 2 раза, а график функции у = 1 2 𝑥2– парабола, полученная из графика функции у=х2 сжатием к оси Ox в 2 раза (рис. 2, 3).
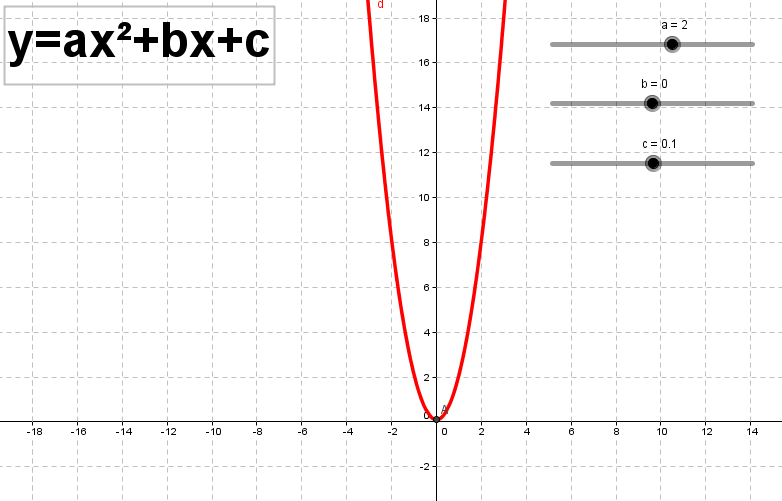
Рис. 2. График функции y=2𝑥2, построенный в среде GeoGebra.
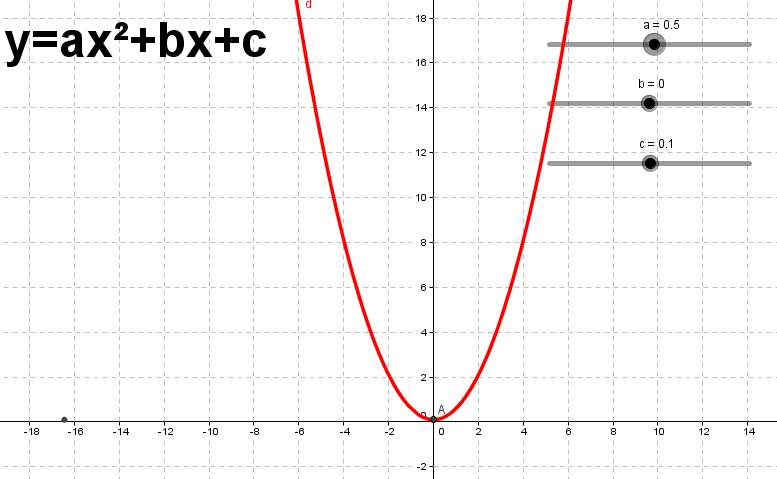
Рис. 3. График функции у = 1 2𝑥2, построенный в среде GeoGebra
В среде GeoGebra надо строить каждый раз новый график. Достаточно установить ползунки для изменения параметров и при передвижении ползунков график будет меняться. Свойства функции y=a𝑥2 при a>0 такие же, как и свойства графика у=х2. График функции y=a𝑥2, где a <0, получается из графика функции с противоположным (положительным) значением а в результате симметрии относительно оси Ox.
На рисунках 4 и 5 изображены графики функций у=−х2 и у=−1 х2.
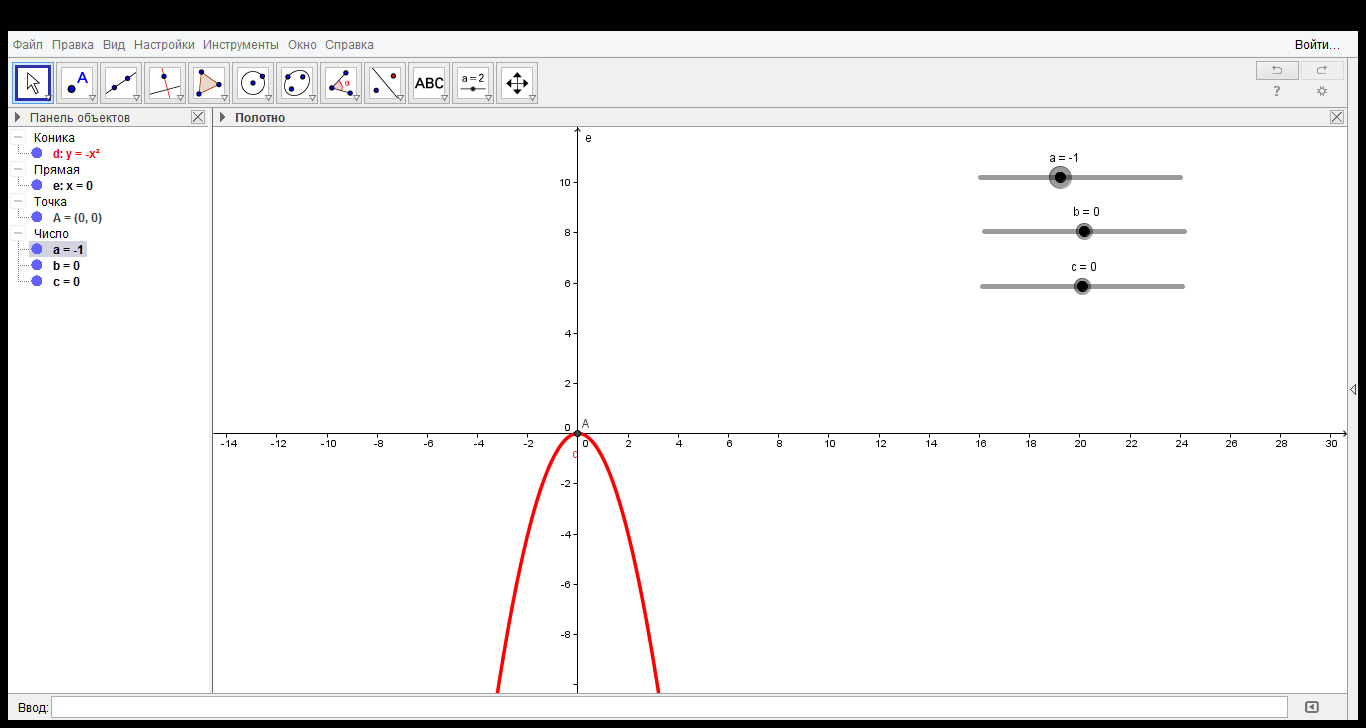
Рис.4. График функции у=−х2, построенный в среде GeoGebra.

Рис. 5. График функции у=− 1
2
х2, построенный в среде GeoGebra.
Свойства графика функции у=−х2:
· Область определения функции – множество всех действительных чисел D(y)=R;
· Область значений функции E(y)=(-∞;0];
· Функция четная;
· y=0 при x=0, y<0 при x>0 и приx<0
· Функция возрастает на промежутке(-∞;0] и убывает на промежутке [0; +∞). Функция имеет наибольшее значение y=0 при x=0.
График функции y=f(x)+n можно получить из графика функции y=f(x) с помощью сдвига вдоль оси Oy на nединиц вверх, если n>0, или на |n| единиц вниз, если n <0, а график функции y=f(x-m) можно получить из графика функции y=f(x) с помощью сдвига графика функции y=f(x) на mединиц вправо, если m>0, или на |m| единиц влево, если m <0.
Поэтому графиком функции вида y=a𝑥2 + 𝑛является парабола с вершиной в точке (0; n), а графиком функции y=a (𝑥 − 𝑚)2–парабола с вершиной в точке (m;0).
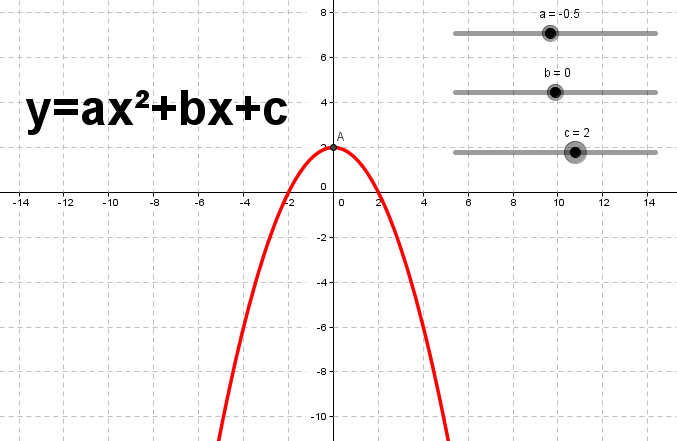
Рис. 6. График функции 𝑦 = −1 2 𝑥2 + 2, построенный в среде GeoGebra 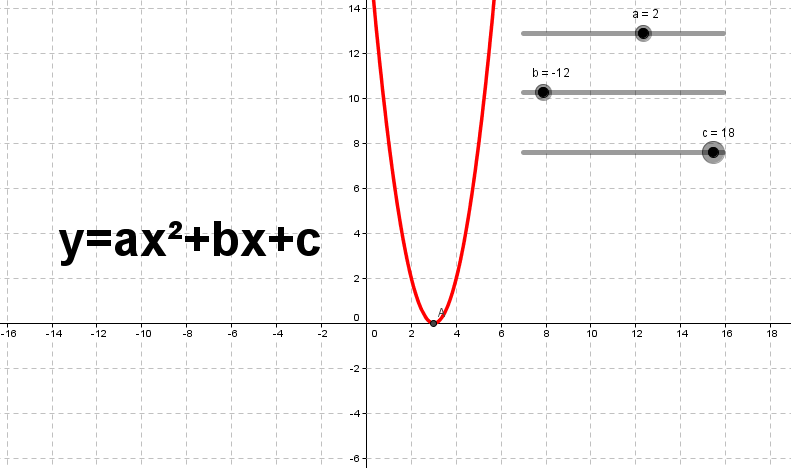
Рис. 7. График функции 𝑦 = 2(𝑥 − 3)2
Любую квадратичную функцию 𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐можно записать формулой вида 𝑦 = 𝑎 (𝑥 − 𝑚)2 + 𝑛, выделив из квадратного трехчлена𝑎𝑥2 + 𝑏𝑥 + 𝑐 квадрат двучлена. Получим:
𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 𝑎 (𝑥 +𝑏 2𝑎)2 −𝐷 2𝑎, где 𝐷 = 𝑏2 − 4𝑎𝑐. Следовательно, график функции 𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 можно получить из графика функции 𝑦 = 𝑎𝑥2 с помощью двух параллельных переносов – сдвига вдоль оси Ox и сдвига вдоль оси Oy.
График функции 𝑦 = 𝑎𝑥2 – парабола. Значит, и графиком функции 𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 является парабола с вершиной в точке (m; n), где 𝑚 = − 𝑏 2𝑎, 𝑛 = − 𝐷 4𝑎. Осью симметрии параболы является прямая x=m.
Учитывая этот вывод, можно схематически изобразить график квадратичной функции. Координаты вершины параболы: 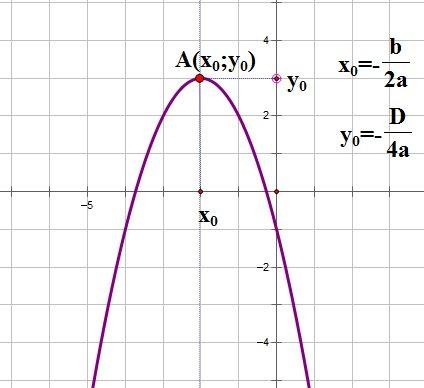
Рис.8. График квадратичной функции, построенный с помощью GeoGebra.
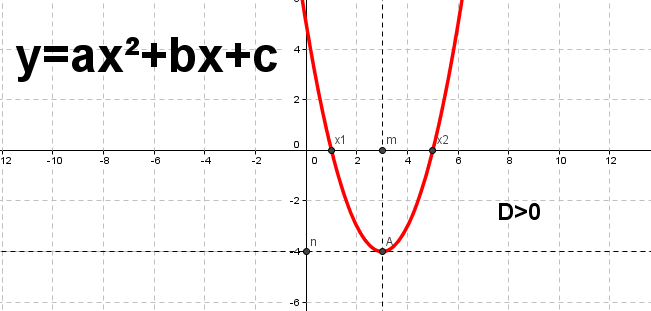
Рис.9. График квадратичной функции, построенный с помощью GeoGebra.

Рис.9. График квадратичной функции, построенный с помощью GeoGebra.
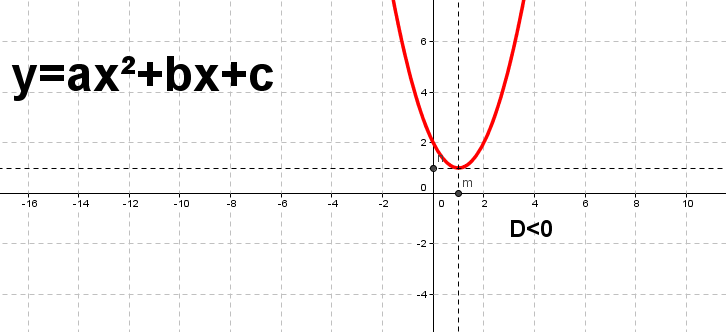
Рис.10. График квадратичной функции, построенный с помощью GeoGebra.
На рисунках 8, 9, 10 показано, какой вид имеют эти графики в зависимости от знака дискриминанта D при a>0. Перечислим свойства функции f(x)=𝑎𝑥2 + 𝑏𝑥 + 𝑐 при a>0: 1. Область определения функции – множество действительных чисел. 2. Если D>0, то функция обращается в нуль при 𝑥1 = −𝑏− 𝐷 2𝑎 и 𝑥2 = −𝑏+ 𝐷 2𝑎. Если D=0, то она обращается в нуль при 𝑥 = − 𝑏 2𝑎. Если D <0, то функция положительна на всей области определения. 3. Если D>0, то функция принимает положительные значения в каждом из промежутков −∞; 𝑥1 и (𝑥2; +∞) и отрицательные значения в промежутке 𝑥1, 𝑥2.
Если D=0, то функция принимает положительные значения при любых x∈R, кроме 𝑥 = − 𝑏 2𝑎.
Если D <0, то функция положительна на всей области определения
4. Функция убывает на промежутке (−∞; − 𝑏 2𝑎]и возрастает на промежутке [− 𝑏 2𝑎; +∞). При 𝑥 = − 𝑏 2𝑎 функция принимает наименьшее значение, равное − 𝐷 4𝑎. 5. Область значений функции – множество [− 𝐷 4𝑎; +∞).
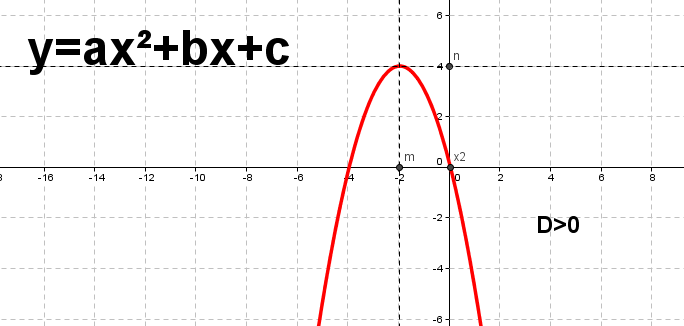
Рис.11. График квадратичной функции, построенный с помощью GeoGebra.
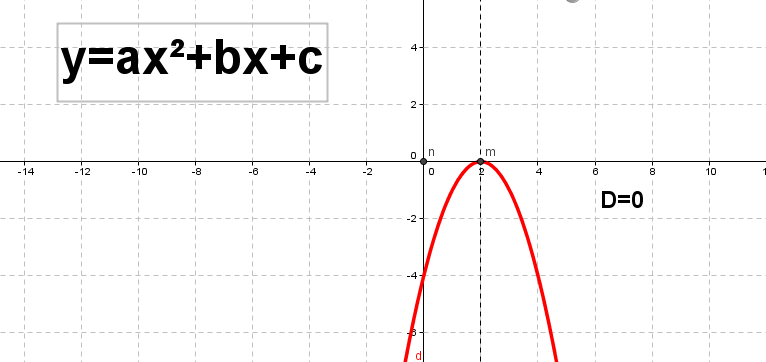
Рис.12. График квадратичной функции, построенный с помощью GeoGebra.
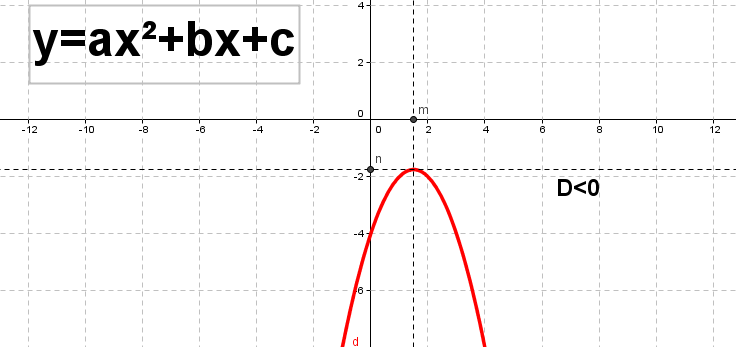
Рис.13. График квадратичной функции, построенный с помощью GeoGebra.
На рисунках 11, 12, 13 показано какой вид имеют графики квадратичной функции при a <0 и в зависимости от знака D. Перечислим свойства функции f(x)=𝑎𝑥2 + 𝑏𝑥 + 𝑐 при a <0: 1. Область определения функции – множество действительных чисел. 2. Если D>0, то функция обращается в нуль при 𝑥1 = −𝑏− 𝐷 2𝑎 и 𝑥2 = −𝑏+ 𝐷 2𝑎. Если D=0, то она обращается в нуль при 𝑥 = − 𝑏 2𝑎.
Если D <0, то функция отрицательна на всей области определения.
3. Если D>0, то функция принимает положительные значения в промежутке 𝑥1, 𝑥2 и отрицательные значения в промежутках −∞; 𝑥1 и (𝑥2; +∞).
Если D=0, то функция принимает отрицательные значения при любых x∈R, кроме 𝑥 = − 𝑏 2𝑎.
Если D <0, то функция отрицательна на всей области определения.
4. Функция возрастает на промежутке (−∞; − 𝑏 2𝑎 ]и убывает на промежутке [− 𝑏 2𝑎; +∞). При 𝑥 = − 𝑏 2𝑎 функция принимает наибольшее значение, равное − 𝐷 4𝑎.
5. Область значений функции – множество (−∞; − 𝐷 4𝑎]. При построении графика квадратичной функции, заданной формулой f(x)=𝑎𝑥2 + 𝑏𝑥 + 𝑐, целесообразно найти нули функции, координаты вершины параболы, координаты точки пересечения параболы с осью Oy и точки, симметричной ей относительно оси симметрии параболы. Затем следует отметить эти точки в координатной плоскости и провести через них плавную непрерывную линию.
Заметим, что в тех случаях, когда парабола не имеет общих точек с осью Ox или пересекает ось Oy в точке, достаточно удаленной от начала координат, для построения параболы используют другие точки, симметричные относительно ее оси. Параметр, полезный при построении графика функции – точка пересечения параболы с осью OY.Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение 𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 вместо х подставить ноль.
Так как ордината (у) любой точки, лежащей на оси Оx равна нулю, чтобы найти координаты точек пересечения графика функции с осью Ox, нужно решить уравнение ах2+вх+с=0.2
Рассмотрим следующие примеры:
Пример 1. Построим графикфункции0.5𝑥2 + 2𝑥 + 2. Найдем нули функции решив уравнение 0.5𝑥2 + 2𝑥 + 2 = 0. 𝐷 = 𝑏2 − 4𝑎𝑐 = 22 − 4 ∗ 0,5 ∗ 2 = 0. Значит парабола пересекает ось Ox в одной точке: 𝑥 = −𝑏 2𝑎 = − 2 1= −2.
Вычислим координаты точек m и n вершины параболы. Абсцисса m равна: 𝑚 = − 𝑏 2𝑎 = − 2 1 = −2. Найдем ординату n, подставив в формулу 𝑓(𝑥) = 0.5𝑥2 + 2𝑥 + 2 вместо x значение m: 𝑛 = 𝑓 −2 = 0,5 ∗ −2 2 + 2 ∗ −2 + 2 = 0 Найдем точку пересечения параболы с осью Oy подставив в уравнение 𝑓(𝑥) = 0.5𝑥2 + 2𝑥 + 2 значение 0 вместо х: 𝑓 0 = 0.5 ∗ 0 + 2 ∗ 0 + 2 = 2 Симметричная ей точка относительно оси симметрии параболы имеет координаты (-4;2). Построим эти точки и, учитывая направление ветвей параболы (вверх), проведем через них непрерывную линию. Получим график функции 𝑦 = 0.5𝑥2 + 2𝑥 + 2.
2Алгебра. 9 класс: учеб.для шк, и кл. с углубл. изуч. математики/Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков.
– 5-е изд. – М.: Мнемозина, 20006. – 439 с. : ил.
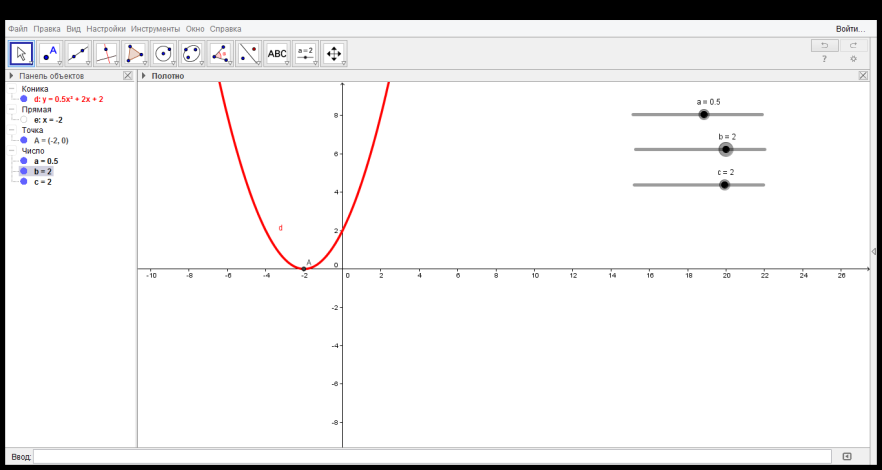
Рис.4. График функции𝑦 = 0.5𝑥2 + 2𝑥 + 2, построенный в среде GeoGebra.
Вывод: квадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами. Первой рассматривается функция у=ах2. Свойства этой функции во многом отличаются от изучаемых ранее случаев линейных функций.
Введение понятия квадратичной функции начинается с решения практической задачи, показывающей зависимость другого рода, отличную от линейной зависимости.
Изучение класса квадратичных функций начинается с изучения функций вида у=ах2; при этом выясняется геометрический смысл коэффициента а. Используя интерактивный объект, учащиеся могут самостоятельно рассмотреть расположение графиков квадратичных функций с разными коэффициентами а и сделать соответствующие выводы.
Построить график функции можно вычислив ее дискриминант, нули функции, координаты вершины параболы, координаты точки пересечения с осью Oy, точку симметричную ей относительно оси симметрии параболы, а можно выделив полный квадрат построить параболу путем сжатия (растяжения), сдвига параболы 𝑦 = 𝑥2.
С помощью программы GeoGebraможно легко построить график любой функции. Причем не обязательно каждый раз строить новый график. Заранее поставив ползунки можно менять значения коэффициентов, график будет меняться. Эту программу очень удобно использовать при объяснении темы
«Квадратичная функция и ее свойства».
Изобразим, зависимость вида параболы от коэффициента.
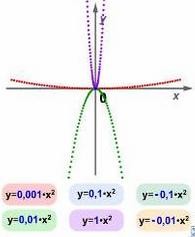
Рис. 11. Графики квадратичных функций.
Для закрепления знаний нужно провести урок на тему «Квадратичная функция. Квадратный трёхчлен» и подробно решить несколько задач по теме «Квадратичная функция» представленных в приложении (приложение1,2).
Заключение
Во время исследования была изучена психолого-педагогическая, методическая и учебная научная литература. Полностью проанализирована тема квадратичной функции. Квадратичная функция является одной из главных функций школьной математики, для которой построена полная теория и доказаны все свойства. Учащиеся должны четко понимать и знать все эти свойства. При этом задач на квадратичную функцию существует великое множество - от очень простых, которые вытекают непосредственно из теории и формул, до самых сложных. Квадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами.
Исследована динамичная средаGeoGebra, которую учителя разных школ могут применять не только для объяснения темы «Квадратичная функция», но и для многих других тем, в которых есть построения и можно продемонстрировать графический метод решения задач.GeoGebra повышает внимание учеников на уроке, их понимание данной темы, а также интерес к предмету в общем. Программу можно использовать для решения задач на интерактивной доске или в компьютерном классе.
Динамичная среда - GeoGebra - это отличное многофункциональное кроссплатформенное математическое приложение, которое станет хорошим помощником всем, кто так или иначе связан в учебе или работе с необходимостью проведения различных математических операций.
При решении задач по теме «Квадратичная функция» большое практическое значение имеет наличие соответствия между алгебраическим описанием задачи и ее геометрической интерпретацией. Именно благодаря этой особенности у нас всегда есть возможность проверить правильность и непротиворечивость своих теоретических рассуждений.
Таким образом, все поставленные цели достигнуты, задачи работы выполнены.
Список использованной литературы
1. Алгебра: сборник заданий для подготовки к итоговой аттестации в 9 кл. Итоговая аттестация / Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович, Л.О. Рослова. - М.: Просвещение, 2006. - С.192.
2. Алгебра: Учеб.для 7 кл, общеобразоват, учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др.- 2-е изд.- М.: Просвещение, 2008. - С.285.
3. Алгебра: Учеб.для 7 кл, общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- 8-е изд.- М.: Просвещение, 2008. - С.207
4. Алгебра: Учеб.для 7 кл, общеобразоват, учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского. - 9- е изд. - М. Просвещение, 2008. - С.223.
5. Алгебра: Учеб.для 8 кл, общеобразоват, учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др.- М.: Просвещение, 2007. - С.287.
6. Алгебра: Учеб.для 8 кл, общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- 44-е изд.- М.: Просвещение: Моск, учеб.», 2008. - С.255.
7. Алгебра: Учеб.для 8 кл, общеобразоват. Учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского. - 3- е изд. - М. Просвещение, 2006. - С. 239.
8. Алгебра: Учеб.для 9 кл, общеобразоват, учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др.- М.: Просвещение, 2008. - С.255.
9. Алгебра: Учеб. Для 9 кл, общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- 10-е изд.- М.: Просвещение: Моск, учеб. 2006. - С.255.
10. Алгебра: Учеб.для 9 кл, общеобразоват, учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского. - 3- е изд. - М. Просвещение, 2006. - С. 271.
11. Алгебра: Учеб, для 9 кл, для школ и кл, с угубл. Изуч, математики / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков - 5-е изд.- М.: Мнемозина, 2006. - С. 439.
12. Печёнкина Е.Н. Практико-ориентированные задачи на уроках математики в основной школе // Электронный ресурс http://rudocs.exdat.com/docs/index.
13. Колягин Ю.М. и Пикан В.В. О прикладной и практической направленности обучения математике: Математика в школе. 1985.
14. Сборник самостоятельных и контрольных работ, автор А.П. Ершова, 2006 год издательство «Илекса» // Электронный ресурс http://rudocs.exdat.com/docs/index.
15. Сборник задач по алгебре. 8-9 классы: пособие для учащихся общеобразовательных учреждений/ М.Л.Галицкий. 15-е изд.- М.: Просвещение, 2010. - С.301.
16. Тесты по математике 5-11 кл. – М.: ООО «Агентство «КРПА
«Олимп»: «Издательство АСТ», 2002. С. 425.
17. Тесты П.И. Алтынов,7-9 класс, 2001 год, издательство «Дрофа».
18. Рубинштейн С. Л. О мышлении и путях его исследования. – М.: Изд-во Акад. наук СССР, 1958. – С.147.
Приложения
Приложение № 1
План-конспект урока алгебры в 9 классе по теме «Квадратичная функция. Квадратный трёхчлен».
Тип урока: обобщение знаний. Цели урока:
1) Обобщение и систематизация знаний, умений и навыков учащихся в построении графиков квадратичной функции, умение применять еѐ свойства, разложение квадратного трёхчлена на множители;
2) развитие чувства гармонии чертежа;
3) развитие исследовательской и познавательной деятельности, самостоятельности и творческой активности, пространственного воображения и логического мышления.
Оборудование: компьютер учителя и школьников, мультимедийный проектор, презентация урока, экран. Программное обеспечение: «PowerPoint», предоставление программы динамичной среды GeoGebraиндивидуально всем школьникам для самостоятельной работы.
План урока:
1. Организационный момент.
2. Математический диктант.
3. Тренировочные упражнения.
4. Самостоятельная работа с применением программы GeoGebra.
5. Итог урока.
6. Домашнее задание.
I. Организационный момент.
Сегодня на уроке мы повторим алгоритмы разложения квадратного трёхчлена на множители, построение графика квадратичной функции, ее свойства и продолжим формирование умений применять эти свойства при выполнении практических заданий.
II. Математический диктант.
1. Определите координаты вершины параболы
2. Составьте уравнение оси симметрии параболы
3. Назовите промежутки, в которых
y > 0, y < 0
4. Назовите промежуток возрастания функции
5. Укажите координаты вершины параболы, заданной формулой:
y = (x + 2)2 - 1
А. (-2; -1) Б. (-2; 1) В. (2; -1) Г. (2; 1).
6. По графику функции y = f (x) определите, какое из утверждений верно:
А. При х=-1 функция принимает наименьшее значение; Б. Функция убывает на промежутке [5; +∞);
В. Функция принимает положительные значения при -1<x <3; Г. Областью значений функции служит промежуток [0;5].
7. С какой прямой график параболы 𝑦 = −𝑥2 + 4𝑥 − 3 не имеет общих точек?
A. y = -10 Б. у = 1 В. у = 0 Г. у = х
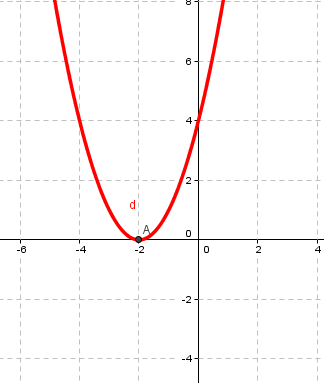
7. График какой функции изображён на рисунке?
A. y=(x+2)2 В. y=-(x+2)2
Б. y=-x2-2 Г. y=-(x–2)2.
III. Тренировочные упражнения.
1. Найдите наименьшее значение квадратного трёхчлена y=2x2+4x-1
2. Найдите наибольшее значение квадратного трёхчлена y=-x2+2x+3.
3. Не выполняя построения, определите, пересекаются ли параболаy =
x2 и прямая у = 5х – 16. Если точки пересечения существуют, найдите их координаты.
IV. Самостоятельная работа. (по вариантам)
1. Сократите дробь:
| 1 вариант | 2 вариант | 3 вариант |
| 12 15 | 21 28 | 4 6 |
2. Разложите на множители квадратный трехчлен
| 1 вариант | 2 вариант | 3 вариант |
| x2 – 8x -9 | x2 – 4x – 96 | -x2 + 3x + 18 |
3. Постройте график функции и опишите еѐ свойства
| 1 вариант | 2 вариант | 3 вариант |
| y = x2 + 4x + 5 | y = x2 - 4x + 1 | y = -x2 + 2x + 2 |
V. Итог урока.
Учитель вместе с учениками разъясняет вопросы:
1. Что такое область определения функции?
2. Что такое множество значений функции?
3. Что такое нули функции?
4. Что такое промежутки убывания функции? 5.Что такое промежутки возрастания функции?
6. Что такое ось симметрии квадратичной функции, по какой формуле вычисляется?
VI. Домашнее задание ученикам.
1.Повторить свойства графика квадратичной функции, алгоритм его построения;
2.Повторить алгоритм разложения квадратного трёхчлена на множители;
3.Стр. 40 №107(б), с. 54 № 183(д).
Приложение № 2
Дата: 2019-02-25, просмотров: 785.