Введение
Развивающее обучение - это обучение, которое непосредственно ориентировано на закономерности развития личности, где развивающий эффект является не побочным, а прямым результатом. Изучение квадратичных функций в средней школе позволяет раскрыть школьникам внутренние связи между понятием функции и другими понятиями школьного курса математики. Кроме того, изучение квадратичной функции расширяет представление учащихся о функции, ее свойствах и графике. Изучение свойств функций имеет огромное развивающее значение для учащихся: они учатся вырабатывать алгоритм действий при решении задач, на основе исследований делают выводы, строят зависимости между величинами.
Актуальность исследуемой работы. Федеральный государственный образовательный стандарт среднего (полного) общего образования, утвержденный приказом Минобразования науки России от 17 апреля 2012 года № 413, предъявляет к результатам обучения курса алгебры и начал математического анализа новые требования, связанные с овладением приемами использования компьютерных программ. Введение ФГОС нового поколения в учебный план способствует оптимизации учебного процесса, разнообразию форм проведения урока, формированию интереса учащихся к математике, кроме того обучение математике по информационно- технологической траектории для подрастающего поколения является ключом к реализации созревающих профильных интересов учащихся, их самовыражению в учении и творческой активности. Именно здесь учащимся разных школ предлагаются разнообразные траектории дополнительного изучения предмета в рамках профильных курсов, факультативов, клубной и проектной деятельности в области информатики.
GeoGebra является динамическим программным обеспечением и геометрической средой предназначенной для построения различных фигур, начиная от простейших парабол, эллипсов заканчивая пространственными
3 D моделями. Сочетание алгебраического, геометрического и числового анализа дает возможность создавать конструкции с точками, линиями, векторами, математическими функциями с возможностью их дальнейшего изменения, то есть полученными объектами учащиеся могут легко манипулировать в пространстве.
Предмет исследования: процесс обучения темы «Квадратичная функция» с использованием среды GeoGebra.
Объект исследования: ученики 9 класса, изучающие тему «Квадратичная функция».
Целью работы является составление соответствующих методических рекомендаций по применению среды GeoGebra при изучении темы «Квадратичная функция».
Для достижения данной цели, были поставлены следующие задачи:
- подбор и анализ учебной литературы;
- подбор и составление практико-ориентированных задач, решаемых в среде GeoGebra по теме «Квадратичная функция» в школьном курсе;
- разработка методических рекомендаций по использованию составленных задач.
Методы исследования:
- изучение и анализ литературы школьного курса математики;
- наблюдение за учебной деятельностью учащихся;
Решение поставленных задач определило структуру курсовой работы. Она состоит из двух глав, введения, заключения и списка использованной литературы, состоящего из 18 изданий, приложения.
Глава 1. Методические особенности изучения темы «Квадратичная функция»
Глава 2.Методическое сопровождение по теме квадратичная функция в школьном курсе
Раздел II . Содержание учебного материала
Цель: расширить сведения о свойствах функций, ознакомить обучающихся со свойствами и графиком квадратичной функции, сформировать умение решать неравенства вида: ах2 + bх+ с>0 и ах2+ bх + с <0
В начале темы рассматриваются сведения о функциях. Повторяются основные понятия: что такое функция? аргумент? область определения функции? график? и т.д., после повторяются понятия о возрастании и убывании функции, промежутках монотонности. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.
Подготовительный шаг к изучению свойств квадратичной функции –это рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квадратного трехчлена, разложении квадратного трехчлена на множители.
Изучать квадратичную функцию будем с рассмотрения функции у=ах2, ее свойств и особенностей графика, а также других частных видов квадратичной функции: у=ах2+n, у=а (х − 𝑚)2. Эти данные нужны при изучении свойств квадратичной функции общего вида. Важно, чтобы ученики поняли, что график функции у = ах2+ bх + с может быть получен из графика функции у = ах2cпомощью двух параллельных переносов. Приёмы построения графика функции у = ах2+ bх + с отрабатываются на конкретных примерах. Здесь особое внимание мы должны уделить формированию у школьников умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.
При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак.
Формирование умений решать неравенства вида ах2+bх+с>0 иах2+bх+с <0, где а не равно 0, осуществляется с опорой на сведения о графике квадратичной функции, где направление ветвей параболы ее расположение относительно оси Ох.
Школьники знакомятся с методом интервалов, с помощью которых можно решить несложные рациональные неравенства. Также они знакомятся со свойствами степенной функции у=𝑥𝑛 при четном и нечетном натуральном показателе n. Вводится понятие корня n-й степени. Они должны понимать смысл записей и иметь представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
Дополнительно школьниками рассматривается степенная функция.
Корень n -й степени, где изучается четная и нечетная функция. Функция
у= 𝑥𝑛 . Определение корня n -й степени. Вычисление корней n -й степени. Таким же образом продолжается изучение свойств функций, рассматриваются свойства степенной функции с натуральным показателем. Изучение корней ограничивается введением понятия корня n -й степени и выполнением несложных заданий на вычисление корней n -й степени, в частности кубических корней.
Раздел III Примерное календарно-тематическое планирование по алгебре для 9 класса на тему «Квадратичная функция»
| № п/п | Тему урока | часы | Тип урока | Элементу содержания | Требования я к уровню подготовленности | Вид контроля | Задание на дом |
| Квадратичная функция. Всего17 часов | |||||||
|
| |||||||
| 1 | Функция | 1 | Актуализация знаний | Функции, область определения и область значения Функции, примеры. | Знать понятие функции, находить их значения, заданных формулам и, таблицей, графиком, решать обратную задачу. | Входной Контроль 20 мин. | п.1. № 3 и 5. |
| 2 | График функции | 1 | Обобщение знаний. | Фронтальный опрос. | п.1. № 15 и 17. | ||
| 3 | Свойства функций, линейной функции, обратной пропорциональности и Контрольная работа | 3 часа | Ознаком ление, закрепле ние и усвоение темы | Возрастание, убывание, свойства функции, свойства обратной пропорцион альности | Текущий, практическая работа и самостоятельная. | п.1 и 2 № 17,1 9, 22,2 4, 33, 25,3 7, 41, 44,4 6б 53,4 6,52 | |
| Квадратичный трехчлен. 5 часов | |||||||
| Квадратичная функция и ее график. 8 часов | |||||||
| Степенная функция. Корень n-ой степени. 4 часа | |||||||
Раздел IV Требования к уровню подготовки учащихся 9 класса на тему «Квадратичная функция»
Учащиеся 9 классов, изучив данную тему, должны уметь определять квадратичную функцию; самостоятельно должны строить и исследовать квадратичную функцию; решать уравнения и системы уравнений графическим способом; определять уравнение параболы по рисунку и определять наименьшее и наибольшее значения функции.
Заключение
Во время исследования была изучена психолого-педагогическая, методическая и учебная научная литература. Полностью проанализирована тема квадратичной функции. Квадратичная функция является одной из главных функций школьной математики, для которой построена полная теория и доказаны все свойства. Учащиеся должны четко понимать и знать все эти свойства. При этом задач на квадратичную функцию существует великое множество - от очень простых, которые вытекают непосредственно из теории и формул, до самых сложных. Квадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами.
Исследована динамичная средаGeoGebra, которую учителя разных школ могут применять не только для объяснения темы «Квадратичная функция», но и для многих других тем, в которых есть построения и можно продемонстрировать графический метод решения задач.GeoGebra повышает внимание учеников на уроке, их понимание данной темы, а также интерес к предмету в общем. Программу можно использовать для решения задач на интерактивной доске или в компьютерном классе.
Динамичная среда - GeoGebra - это отличное многофункциональное кроссплатформенное математическое приложение, которое станет хорошим помощником всем, кто так или иначе связан в учебе или работе с необходимостью проведения различных математических операций.
При решении задач по теме «Квадратичная функция» большое практическое значение имеет наличие соответствия между алгебраическим описанием задачи и ее геометрической интерпретацией. Именно благодаря этой особенности у нас всегда есть возможность проверить правильность и непротиворечивость своих теоретических рассуждений.
Таким образом, все поставленные цели достигнуты, задачи работы выполнены.
Список использованной литературы
1. Алгебра: сборник заданий для подготовки к итоговой аттестации в 9 кл. Итоговая аттестация / Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович, Л.О. Рослова. - М.: Просвещение, 2006. - С.192.
2. Алгебра: Учеб.для 7 кл, общеобразоват, учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др.- 2-е изд.- М.: Просвещение, 2008. - С.285.
3. Алгебра: Учеб.для 7 кл, общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- 8-е изд.- М.: Просвещение, 2008. - С.207
4. Алгебра: Учеб.для 7 кл, общеобразоват, учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского. - 9- е изд. - М. Просвещение, 2008. - С.223.
5. Алгебра: Учеб.для 8 кл, общеобразоват, учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др.- М.: Просвещение, 2007. - С.287.
6. Алгебра: Учеб.для 8 кл, общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- 44-е изд.- М.: Просвещение: Моск, учеб.», 2008. - С.255.
7. Алгебра: Учеб.для 8 кл, общеобразоват. Учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского. - 3- е изд. - М. Просвещение, 2006. - С. 239.
8. Алгебра: Учеб.для 9 кл, общеобразоват, учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др.- М.: Просвещение, 2008. - С.255.
9. Алгебра: Учеб. Для 9 кл, общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- 10-е изд.- М.: Просвещение: Моск, учеб. 2006. - С.255.
10. Алгебра: Учеб.для 9 кл, общеобразоват, учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского. - 3- е изд. - М. Просвещение, 2006. - С. 271.
11. Алгебра: Учеб, для 9 кл, для школ и кл, с угубл. Изуч, математики / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков - 5-е изд.- М.: Мнемозина, 2006. - С. 439.
12. Печёнкина Е.Н. Практико-ориентированные задачи на уроках математики в основной школе // Электронный ресурс http://rudocs.exdat.com/docs/index.
13. Колягин Ю.М. и Пикан В.В. О прикладной и практической направленности обучения математике: Математика в школе. 1985.
14. Сборник самостоятельных и контрольных работ, автор А.П. Ершова, 2006 год издательство «Илекса» // Электронный ресурс http://rudocs.exdat.com/docs/index.
15. Сборник задач по алгебре. 8-9 классы: пособие для учащихся общеобразовательных учреждений/ М.Л.Галицкий. 15-е изд.- М.: Просвещение, 2010. - С.301.
16. Тесты по математике 5-11 кл. – М.: ООО «Агентство «КРПА
«Олимп»: «Издательство АСТ», 2002. С. 425.
17. Тесты П.И. Алтынов,7-9 класс, 2001 год, издательство «Дрофа».
18. Рубинштейн С. Л. О мышлении и путях его исследования. – М.: Изд-во Акад. наук СССР, 1958. – С.147.
Приложения
Приложение № 1
План-конспект урока алгебры в 9 классе по теме «Квадратичная функция. Квадратный трёхчлен».
Тип урока: обобщение знаний. Цели урока:
1) Обобщение и систематизация знаний, умений и навыков учащихся в построении графиков квадратичной функции, умение применять еѐ свойства, разложение квадратного трёхчлена на множители;
2) развитие чувства гармонии чертежа;
3) развитие исследовательской и познавательной деятельности, самостоятельности и творческой активности, пространственного воображения и логического мышления.
Оборудование: компьютер учителя и школьников, мультимедийный проектор, презентация урока, экран. Программное обеспечение: «PowerPoint», предоставление программы динамичной среды GeoGebraиндивидуально всем школьникам для самостоятельной работы.
План урока:
1. Организационный момент.
2. Математический диктант.
3. Тренировочные упражнения.
4. Самостоятельная работа с применением программы GeoGebra.
5. Итог урока.
6. Домашнее задание.
I. Организационный момент.
Сегодня на уроке мы повторим алгоритмы разложения квадратного трёхчлена на множители, построение графика квадратичной функции, ее свойства и продолжим формирование умений применять эти свойства при выполнении практических заданий.
II. Математический диктант.
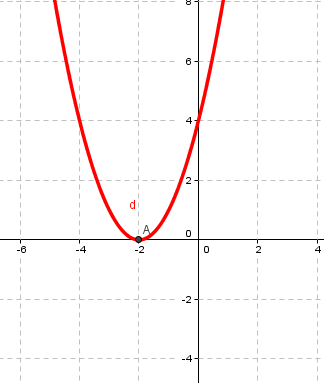
1. Определите координаты вершины параболы
2. Составьте уравнение оси симметрии параболы
3. Назовите промежутки, в которых
y > 0, y < 0
4. Назовите промежуток возрастания функции
5. Укажите координаты вершины параболы, заданной формулой:
y = (x + 2)2 - 1
А. (-2; -1) Б. (-2; 1) В. (2; -1) Г. (2; 1).
6. По графику функции y = f (x) определите, какое из утверждений верно:
А. При х=-1 функция принимает наименьшее значение; Б. Функция убывает на промежутке [5; +∞);
В. Функция принимает положительные значения при -1<x <3; Г. Областью значений функции служит промежуток [0;5].
7. С какой прямой график параболы 𝑦 = −𝑥2 + 4𝑥 − 3 не имеет общих точек?
A. y = -10 Б. у = 1 В. у = 0 Г. у = х
7. График какой функции изображён на рисунке?
A. y=(x+2)2 В. y=-(x+2)2
Б. y=-x2-2 Г. y=-(x–2)2.
III. Тренировочные упражнения.
1. Найдите наименьшее значение квадратного трёхчлена y=2x2+4x-1
2. Найдите наибольшее значение квадратного трёхчлена y=-x2+2x+3.
3. Не выполняя построения, определите, пересекаются ли параболаy =
x2 и прямая у = 5х – 16. Если точки пересечения существуют, найдите их координаты.
IV. Самостоятельная работа. (по вариантам)
1. Сократите дробь:
| 1 вариант | 2 вариант | 3 вариант |
| 12 15 | 21 28 | 4 6 |
2. Разложите на множители квадратный трехчлен
| 1 вариант | 2 вариант | 3 вариант |
| x2 – 8x -9 | x2 – 4x – 96 | -x2 + 3x + 18 |
3. Постройте график функции и опишите еѐ свойства
| 1 вариант | 2 вариант | 3 вариант |
| y = x2 + 4x + 5 | y = x2 - 4x + 1 | y = -x2 + 2x + 2 |
V. Итог урока.
Учитель вместе с учениками разъясняет вопросы:
1. Что такое область определения функции?
2. Что такое множество значений функции?
3. Что такое нули функции?
4. Что такое промежутки убывания функции? 5.Что такое промежутки возрастания функции?
6. Что такое ось симметрии квадратичной функции, по какой формуле вычисляется?
VI. Домашнее задание ученикам.
1.Повторить свойства графика квадратичной функции, алгоритм его построения;
2.Повторить алгоритм разложения квадратного трёхчлена на множители;
3.Стр. 40 №107(б), с. 54 № 183(д).
Приложение № 2
Проверка:
𝑦 = −𝑥2 − 4𝑥 + 1 = − 𝑥2 + 4𝑥 + 4 + 5 = − 𝑥 + 2 2 + 5 ≤ 5;
Наибольшее значение функции y=5, при x=-2;
Ответ: (-2;5)
Введение
Развивающее обучение - это обучение, которое непосредственно ориентировано на закономерности развития личности, где развивающий эффект является не побочным, а прямым результатом. Изучение квадратичных функций в средней школе позволяет раскрыть школьникам внутренние связи между понятием функции и другими понятиями школьного курса математики. Кроме того, изучение квадратичной функции расширяет представление учащихся о функции, ее свойствах и графике. Изучение свойств функций имеет огромное развивающее значение для учащихся: они учатся вырабатывать алгоритм действий при решении задач, на основе исследований делают выводы, строят зависимости между величинами.
Актуальность исследуемой работы. Федеральный государственный образовательный стандарт среднего (полного) общего образования, утвержденный приказом Минобразования науки России от 17 апреля 2012 года № 413, предъявляет к результатам обучения курса алгебры и начал математического анализа новые требования, связанные с овладением приемами использования компьютерных программ. Введение ФГОС нового поколения в учебный план способствует оптимизации учебного процесса, разнообразию форм проведения урока, формированию интереса учащихся к математике, кроме того обучение математике по информационно- технологической траектории для подрастающего поколения является ключом к реализации созревающих профильных интересов учащихся, их самовыражению в учении и творческой активности. Именно здесь учащимся разных школ предлагаются разнообразные траектории дополнительного изучения предмета в рамках профильных курсов, факультативов, клубной и проектной деятельности в области информатики.
GeoGebra является динамическим программным обеспечением и геометрической средой предназначенной для построения различных фигур, начиная от простейших парабол, эллипсов заканчивая пространственными
3 D моделями. Сочетание алгебраического, геометрического и числового анализа дает возможность создавать конструкции с точками, линиями, векторами, математическими функциями с возможностью их дальнейшего изменения, то есть полученными объектами учащиеся могут легко манипулировать в пространстве.
Предмет исследования: процесс обучения темы «Квадратичная функция» с использованием среды GeoGebra.
Объект исследования: ученики 9 класса, изучающие тему «Квадратичная функция».
Целью работы является составление соответствующих методических рекомендаций по применению среды GeoGebra при изучении темы «Квадратичная функция».
Для достижения данной цели, были поставлены следующие задачи:
- подбор и анализ учебной литературы;
- подбор и составление практико-ориентированных задач, решаемых в среде GeoGebra по теме «Квадратичная функция» в школьном курсе;
- разработка методических рекомендаций по использованию составленных задач.
Методы исследования:
- изучение и анализ литературы школьного курса математики;
- наблюдение за учебной деятельностью учащихся;
Решение поставленных задач определило структуру курсовой работы. Она состоит из двух глав, введения, заключения и списка использованной литературы, состоящего из 18 изданий, приложения.
Глава 1. Методические особенности изучения темы «Квадратичная функция»
Дата: 2019-02-25, просмотров: 603.