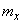В главе 5 мы ввели в рассмотрение числовые характеристики одной случайной величины - начальные и центральные моменты различных порядков. Из этих характеристик важнейшими являются две: математическое ожидание и дисперсия .

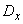Аналогичные числовые характеристики - начальные и центральные моменты различных порядков - можно ввести и для системы двух случайных величин.

Начальным моментом порядка 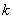, 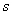системы 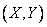называется математическое ожидание произведения 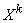на :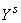

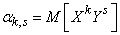. (8.6.1)

Центральным моментом порядка 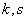системы 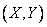называется математическое ожидание произведения 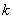-й и 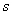-й степени соответствующих центрированных величин:

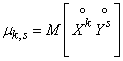, (8.6.2)

где , .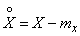

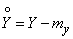Выпишем формулы, служащие для непосредственного подсчета моментов. Для прерывных случайных величин

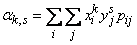, (8.6.3)

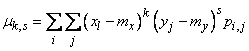, (8.6.4)

где 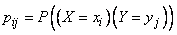— вероятность того, что система 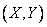примет значения 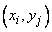, а суммирование распространяется по всем возможным значениям случайных величин , .

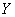Для непрерывных случайных величин:

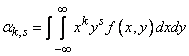, (8.6.5)

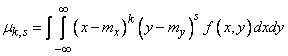, (8.6.6)

где - плотность распределения системы.

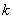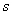Помимо и , характеризующих порядок момента по отношению к отдельным величинам, рассматривается еще суммарный порядок момента 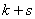, равный сумме показателей степеней при и 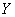. Соответственно суммарному порядку моменты классифицируются на первые, вторые и т. д. На практике обычно применяются только первые и вторые моменты.

Первые начальные моменты представляют собой уже известные нам математические ожидания величин и 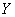, входящих в систему:

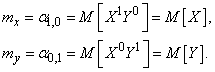
Совокупность математических ожиданий 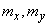представляет собой характеристику положения системы. Геометрически это координаты средней точки на плоскости, вокруг которой происходит рассеивание точки .

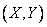Кроме первых начальных моментов, на практике широко применяются еще вторые центральные моменты системы. Два из них представляют собой уже известные нам дисперсии величин и :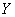

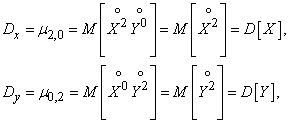
характеризующие рассеивание случайной точки в направлении осе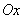й и .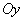

Особую роль как характеристика системы играет второй смешанный центральный момент:

,

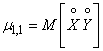т.е. математическое ожидание произведения центрированных величин.

Ввиду того, что этот момент играет важную роль в теории, введем для него особое обозначение:

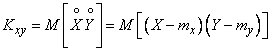. (8.6.7)

Характеристика 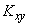называется корреляционным моментом (иначе — «моментом связи») случайных величин , .

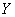Для прерывных случайных величин корреляционный момент выражается формулой

, (8.6.8)

а для непрерывных - формулой

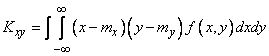. (8.6.9)

Выясним смысл и назначение этой характеристики.

Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо, рассеивания величин и 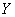, еще и связь между ними. Для того чтобы убедиться в этом, докажем, что для независимыхслучайных величин корреляционный момент равен нулю.

Доказательство проведем для непрерывных случайных величин. Пусть , 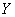- независимые непрерывные величины с плотностью распределения . В 8.5 мы доказали, что для независимых величин

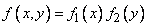. (8.6.10)

где 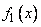, 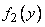- плотности распределения соответственно величин и .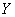

Подставляя выражение (8.6.10) в формулу (8.6.9), видим, что интеграл (8.6.9) превращается в произведение двух интегралов:

.

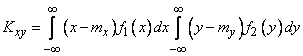Интеграл

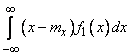
представляет собой не что иное, как первый центральный момент величины , и, следовательно, равен нулю; по той же причине равен нулю и второй сомножитель; следовательно, для независимых случайных величин .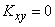

Таким образам, если корреляционный момент двух случайных величин отличен от нуля, это есть признак наличия зависимости между ними.

Из формулы (8.6.7) видно, что корреляционный момент характеризует не только зависимость величин, но и их рассеивание. Действительно, если, например, одна из величин 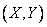весьма мало отклоняется от своего математического ожидания (почти не случайна), то корреляционный момент будет мал, какой бы тесной зависимостью ни были связаны величины 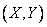. Поэтому для характеристики связи между величинами 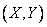в чистом виде переходят от момента 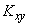к безразмерной характеристике

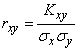, (8.6.11)

где 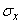, 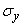- средние квадратические отклонения величин , 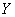. Эта характеристика называется коэффициентом корреляции величин и 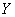. Очевидно, коэффициент корреляции обращается в ноль одновременно с корреляционным моментом; следовательно, для независимых случайных величин коэффициент корреляции равен нулю.

Случайные величины, для которых корреляционный момент (а значит, и коэффициент корреляции) равен нулю, называются некоррелированными (иногда – «несвязанными»).

Выясним, эквивалентно ли понятие некоррелированности случайных величин понятию независимости. Выше мы доказали, что две независимые случайные величины всегда являются некоррелированными. Остается выяснить: справедливо ли обратное положение, вытекает ли из некоррелированности величин их независимость? Оказывается - нет. Можно построить примеры таких случайных величин, которые являются некоррелированными, но зависимыми. Равенство нулю коэффициента корреляции - необходимое, но не достаточное условие независимости случайных величин. Из независимости случайных величин вытекает их некоррелированность; напротив, из некоррелированности величин еще не следует их независимость. Условие независимости случайных величин – более жесткое, чем условие некоррелированности.

Убедимся в этом на примере. Рассмотрим систему случайных величин 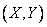, распределенную с равномерной плотностью внутри круга 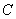радиуса 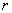с центром в начале координат (рис.8.6.1).

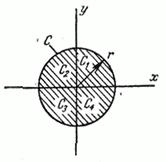
Рис.8.6.1

Плотность распределения величин 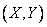выражается формулой

Из условия 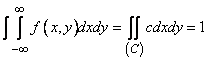находим .

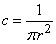Нетрудно убедиться, что в данном примере величины являются зависимыми. Действительно, непосредственно ясно, что если величина приняла, например, значение 0, то величина 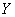может с равной вероятностью принимать все значения от 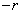до 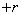; если же величина приняла значение 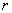, то величина 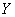может принять только одно-единственное значение, в точности равное нулю; вообще, диапазон возможных значений 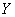зависит от того, какое значение приняла .

Посмотрим, являются ли эти величины коррелированными. Вычислим корреляционный момент. Имея в виду, что по соображениям симметрии 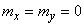, получим:

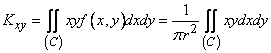. (8.6.12)

Для вычисления интеграла разобьем область интегрирования (круг 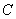) на четыре сектора 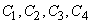, соответствующие четырем координатным углам. В секторах 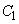и 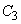подынтегральная функция положительна, в секторах 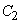и 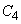- отрицательна; по абсолютной же величине интегралы по этим секторам равны; следовательно, интеграл (8.6.12) равен нулю, и величины 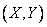не коррелированы.

Таким образом, мы видим, что из некоррелированности случайных величин не всегда следует их независимость.

Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную зависимость. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или же убывать) по линейному закону. Эта тенденция к линейной зависимости может быть более или менее ярко выраженной, более или менее приближаться к функциональной, т. е. самой тесной линейной зависимости. Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами. Если случайные величины и 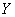связаны точной линейной функциональной зависимостью:

.

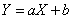то 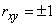, причем знак «плюс» или «минус» берется в зависимости от того, положителен или отрицателен коэффициент 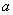. В общем случае, когда величины и 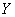связаны произвольной вероятностной зависимостью, коэффициент корреляции может иметь значение в пределах:

.

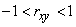В случае 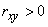говорят о положительной корреляции величин и 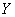, в случае 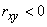- об отрицательной корреляции. Положительная корреляция между случайными величинами означает, что при возрастании одной из них другая имеет тенденцию в среднем возрастать; отрицательная корреляция означает, что при возрастании одной из случайных величин другая имеет тенденцию в среднем убывать.

В рассмотренном примере двух случайных величин 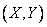, распределенных внутри круга с равномерной плотностью, несмотря на наличие зависимости между и 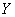, линейная зависимость отсутствует; при возрастании меняется только диапазон изменения 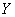, а его среднее значение не меняется; естественно, величины оказываются некоррелированными.

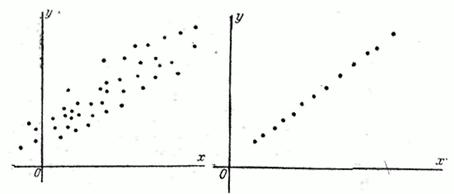
Рис. 8.6.2 Рис.8.6.3

Приведем несколько примеров случайных величин с положительной и отрицательной корреляцией.

1. Вес и рост человека связаны положительной корреляцией.

2. Время, потраченное на регулировку прибора при подготовке его к работе, и время его безотказной работы связаны положительной корреляцией (если, разумеется, время потрачено разумно). Наоборот, время, потраченное на подготовку, и количество неисправностей, обнаруженное при работе прибора, связаны отрицательной корреляцией.

3. При стрельбе залпом координаты точек попадания отдельных снарядов связаны положительной корреляцией (так как имеются общие для всех выстрелов ошибки прицеливания, одинаково отклоняющие от цели каждый из них).

4. Производится два выстрела по цели; точка попадания первого выстрела регистрируется, и в прицел вводится поправка, пропорциональная ошибке первого выстрела с обратным знаком. Координаты точек попадания первого и второго выстрелов будут связаны отрицательной корреляцией.

Если в нашем распоряжении имеются результаты ряда опытов над системой случайных величин , то о наличии или отсутствии существенной корреляции между ними легко судить в первом приближении по графику, на котором изображены в виде точек все полученные из опыта пары значений случайных величин. Например, если наблюденные пары значений величин расположились так, как показано на рис. 8.6.2, то это указывает на наличие явно выраженной положительной корреляции между величинами. Еще более ярко выраженную положительную корреляцию, близкую к линейной функциональной зависимости, наблюдаем на рис. 8.6.3. На рис. 8.6.4 показан случай сравнительно слабой отрицательной корреляции. Наконец, на рис. 8.6.5 иллюстрируется случай практически некоррелированных случайных величин. На практике, перед тем, как исследовать корреляцию случайных величин, всегда полезно предварительно построить наблюденные пары значений на графике для первого качественного суждения о типе корреляции.

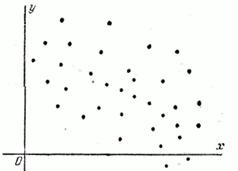
Рис. 8.6.4 Рис. 8.6.5

Способы определения характеристик системы случайных величин из опытов будут освещены в гл.14.

ОБРАБОТКА ОПЫТОВ

В главе 7 мы уже рассмотрели некоторые задачи математической статистики, относящиеся к обработке опытных данных. Это были главным образом задачи о нахождении законов распределения случайных величии по результатам опытов. Чтобы найти закон распределения, нужно располагать достаточно обширным статистическим материалом, порядка нескольких сотен опытов (наблюдений). Однако на практике часто приходится иметь дело со статистическим материалом весьма ограниченного объема - с двумя-тремя десятками наблюдении, часто даже меньше. Это обычно связано с дороговизной и сложностью постановки каждого опыта. Такого ограниченного материала явно недостаточно для того, чтобы найти заранее неизвестный закон распределения случайной величины; но все же этот материал может быть обработан и использован для получения некоторых сведений о случайной величине. Например, на основе ограниченного статистического материала можно определить - хотя бы ориентировочно - важнейшие числовые характеристики случайной величины: математическое ожидание, дисперсию, иногда - высшие моменты. На практике часто бывает, что вид закона распределения известен заранее, а требуется найти только некоторые параметры, от которых он зависит. Например, если заранее известно, что закон распределения случайной величины нормальный, то задача обработки сводится к определению двух его параметров 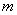и 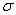. Если заранее известно, что величина распределена по закону Пуассона, то подлежит определению только один его параметр: математическое ожидание 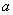. Наконец, в некоторых задачах вид закона распределения вообще несуществен, а требуется знать только его числовые характеристики.

В данной главе мы рассмотрим ряд задач об определении неизвестных параметров, от которых зависит закон распределения случайной величины, но ограниченному числу опытов.

Прежде всего нужно отметить, что любое значение искомого параметра, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайности. Такое приближенное, случайное значение мы будем называть оценкой параметра. Например, оценкой для математического ожидания может служить среднее арифметическое наблюденных значений случайной величины в 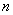независимых опытах. При очень большом числе опытов среднее арифметическое будет с большой вероятностью весьма близко к математическому ожиданию. Если же число опытов 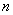невелико, то замена математического ожидания средним арифметическим приводит к какой-то ошибке. Эта ошибка в среднем тем больше, чем меньше число опытов. Так же будет обстоять дело и с оценками других неизвестных параметров. Любая из таких оценок случайна; при пользовании ею неизбежны ошибки. Желательно выбрать такую оценку, чтобы эти ошибки были по возможности минимальными.

Рассмотрим следующую общую задачу. Имеется случайная величина , закон распределения которой содержит неизвестный параметр 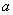. Требуется найти подходящую оценку для параметра 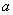по результатам 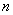независимых опытов, в каждом из которых величина приняла определенное значение.

Обозначим наблюденные значения случайной величины

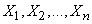. (14.1.1)

Их можно рассматривать как 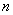«экземпляров» случайной величины , то есть 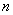независимых случайных величин, каждая из которых распределена по тому же закону, что и случайная величина .

Обозначим оценку для параметра 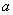. Любая оценка, вычисляемая на основе материала (14.1.1), должна представлять собой функцию величин :

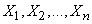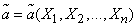(14.1.2)

и, следовательно, сама является величиной случайной. Закон распределения зависит, во-первых, от закона распределения величины (и, в частности, от самого неизвестного параметра 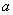); во-вторых, от числа опытов 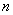. В принципе этот закон распределения может быть найден известными методами теории вероятностей.

Предъявим к оценке ряд требований, которым она должна удовлетворять, чтобы быть в каком-то смысле «доброкачественной» оценкой.

Естественно потребовать от оценки , чтобы при увеличении числа опытов 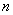она приближалась (сходилась повероятности) к параметру 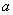. Оценка, обладающая таким свойством, называется состоятельной.

Кроме того, желательно, чтобы, пользуясь величиной вместо 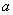, мы по крайней мере не делали систематической ошибки в сторону завышения или занижения, т. е. чтобы выполнялось условие

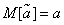. (14.1.3)

Оценка, удовлетворяющая такому условию, называется несмещенной.

Наконец, желательно, чтобы выбранная несмещенная оценка обладала по сравнению с другими наименьшейдисперсией, т. е.

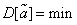. (14.1.4)

Оценка, обладающая таким свойством, называется эффективной.

На практике не всегда удается удовлетворить всем этим требованиям. Например, может оказаться, что, даже еслиэффективная оценка существует, формулы для ее вычисления оказываются слишком сложными, и приходится удовлетворяться другой оценкой, дисперсия которой несколько больше. Иногда применяются - в интересах простоты расчетов - незначительно смещенные оценки. Однако выбору оценки всегда должно предшествовать ее критическое рассмотрение со всех перечисленных выше точек зрения.