Формула Байеса
Пусть событие  происходит одновременно с одним из
происходит одновременно с одним из  несовместных событий
несовместных событий 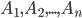 . Требуется найти вероятность события
. Требуется найти вероятность события  , если известно, что событие
, если известно, что событие  произошло.
произошло.
На основании теоремы о вероятности произведения двух событий можно написать
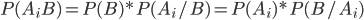
Откуда
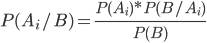
или
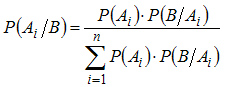 (3.2)
(3.2)
Формула (3.2) носит название формулы Байеса.
Пример. Три организации представили в контрольное управление счета для выборочной проверки. Первая организация представила 15 счетов, вторая — 10, третья — 25. Вероятности правильного оформления счетов у этих организаций известны и соответственно равны: 0,9; 0,8; 0,85. Был выбран один счет и он оказался правильным. Определить вероятность того, что этот счет принадлежит второй организации.
Решение. Пусть 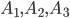 — события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут
— события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут
 ,
,  ,
, 
По формуле полной вероятности определяем вероятность выбора правильно оформленного счета

По формуле Байеса находим исходную вероятность
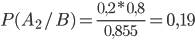
Задача 1.
Монету подбрасывают 10 раз. Какова вероятность того, что при десятикратном подбрасывании монеты герб выпадет 3 раза?
Решение. Число испытаний n=10 невелико, поэтому вероятность можно вычислить непосредственно по формуле Бернулли:
P10(3) = С103 p3 q10-3, где С103 = 10! / 3!(10-3)! = 120, р=1/2, q=1-р=1/2.
P10(3) = 120*(1/2)3*(1/2)7=120*1/210=120/1024=15/128≈0,117
7. оставим теперь более общую задачу.
Рассмотрим последовательность n независимых испытаний в каждом из которых может произойти или не произойти некоторое событие А. При этом вероятность появления события в каждом испытании различна.
Обозначим через 
 . Аi – событие состоящее том что А произойдет в i-ом испытании
. Аi – событие состоящее том что А произойдет в i-ом испытании  – событие состоящее том что А не произойдет в i-ом испытании соответственно.
– событие состоящее том что А не произойдет в i-ом испытании соответственно.
Следует определить вероятность того что событие А произойдет m раз в серии из n испытаний.
Обозначим через Вm – событие состоящее в том что, событие А произойдет m раз в серии из n испытаний.

| (2.2.1) |
Здесь Аi – событие состоящее в том, что событие А произойдет в i- ом испытании. Событие Вmпредставляет собой сумму несовместных событий, поэтому
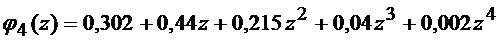
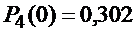
Число слагаемых в выражении равно  , но они все различные. Для вычисления
, но они все различные. Для вычисления 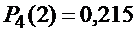 используют производящую функцию
используют производящую функцию
ProizFunc
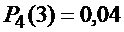
| (2.2.2) |
Зададимся целью найти в этом произведении коэффициент 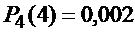 при
при  . Для этого перемножим биномы и произведем приведение подобных членов. Каждый член содержащий
. Для этого перемножим биномы и произведем приведение подобных членов. Каждый член содержащий  будет иметь в качестве коэффициента произведение m букв p с какими-то индексами и n-m букв q с другими оставшимися индексами, а после приведения подобных членов коэффициент при
будет иметь в качестве коэффициента произведение m букв p с какими-то индексами и n-m букв q с другими оставшимися индексами, а после приведения подобных членов коэффициент при  будет представлять собой сумму всех возможных произведений такого типа.
будет представлять собой сумму всех возможных произведений такого типа.
Таким образом, вероятность того, что событие А произойдет m раз в серии из n испытаний равна коэффициенту при  в выражении производящей функции, то есть
в выражении производящей функции, то есть
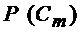
| (2.2.3) |

| (2.2.4) |
Если производятся n независимых опытов в различных условиях, причем вероятность появления события А в i-м опыте равна 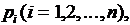 то вероятность Р
то вероятность Р 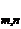 того, что событие А в n опытах появится m раз, равна коэффициенту при Z
того, что событие А в n опытах появится m раз, равна коэффициенту при Z 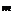 в разложении по степеням Z производящей функции
в разложении по степеням Z производящей функции  где
где 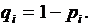
8 Данная статья является естественным продолжением урока о независимых испытаниях, на котором мы познакомились с формулой Бернулли и отработали типовые примеры по теме. Локальная и интегральная теоремы Лапласа (Муавра-Лапласа) решают аналогичную задачу с тем отличием, что они применимы к достаточно большому количеству независимых испытаний. Не нужно тушеваться слов «локальная», «интегральная», «теоремы» – материал осваивается с той же лёгкостью, с какой Лаплас потрепал кучерявую голову Наполеона. Поэтому безо всяких комплексов и предварительных замечаний сразу же рассмотрим демонстрационный пример:
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет 200 раз.
По характерным признакам здесь следует применить формулу Бернулли  . Вспомним смысл этих букв:
. Вспомним смысл этих букв:
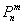 – вероятность того, что в
– вероятность того, что в  независимых испытаниях случайное событие
независимых испытаниях случайное событие  наступит ровно
наступит ровно 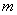 раз;
раз;
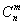 – биномиальный коэффициент;
– биномиальный коэффициент;
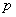 – вероятность появления события
– вероятность появления события  в каждом испытании;
в каждом испытании;
 – вероятность противоположного события.
– вероятность противоположного события.
Применительно к нашей задаче:
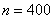 – общее количество испытаний;
– общее количество испытаний;
 – количество бросков, в которых должен выпасть орёл;
– количество бросков, в которых должен выпасть орёл;
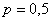 – вероятность выпадения орла в каждом броске;
– вероятность выпадения орла в каждом броске;
 – вероятность выпадения решки.
– вероятность выпадения решки.
Таким образом, вероятность того, что в результате 400 бросков монеты орёл выпадет ровно 200 раз: 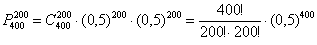 …Стоп, что делать дальше? Микрокалькулятор (по крайне мере, мой) не справился с 400-й степенью и капитулировал перед факториалами. А считать через произведение что-то не захотелось =) Воспользуемся стандартной функцией Экселя, которая сумела обработать монстра:
…Стоп, что делать дальше? Микрокалькулятор (по крайне мере, мой) не справился с 400-й степенью и капитулировал перед факториалами. А считать через произведение что-то не захотелось =) Воспользуемся стандартной функцией Экселя, которая сумела обработать монстра: 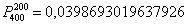 .
.
Заостряю ваше внимание, что получено точное значение и такое решение вроде бы идеально. На первый взгляд. Перечислим веские контраргументы:
– во-первых, программного обеспечения может не оказаться под рукой;
– и во-вторых, решение будет смотреться нестандартно (с немалой вероятностью придётся перерешивать);
Поэтому, уважаемые читатели, в ближайшем будущем нас ждёт:
Локальная теорема Лапласа
Если вероятность 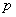 появления случайного события
появления случайного события  в каждом испытании постоянна, то вероятность
в каждом испытании постоянна, то вероятность 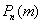 того, что в
того, что в  испытаниях событие
испытаниях событие  наступит ровно
наступит ровно 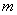 раз, приближённо равна:
раз, приближённо равна:
 , где
, где 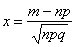 .
.
При этом, чем больше  , тем рассчитанная вероятность
, тем рассчитанная вероятность 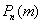 будет лучше приближать точное значению
будет лучше приближать точное значению 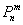 , полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат
, полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат 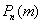 может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность
может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность 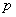 ближе к 0,5, и наоборот – даёт существенную погрешность при значениях
ближе к 0,5, и наоборот – даёт существенную погрешность при значениях 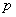 , близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы
, близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы  является выполнение неравенства
является выполнение неравенства 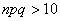 (
( 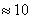 ).
).
Так, например, если  , то
, то 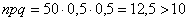 и применение теоремы Лапласа для 50 испытаний оправдано. Но если
и применение теоремы Лапласа для 50 испытаний оправдано. Но если 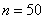 и
и 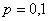 , то
, то 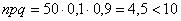 и приближение
и приближение 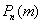 (к точному значению
(к точному значению 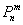 ) будет плохим.
) будет плохим.
О том, почему 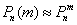 и об особенной функции
и об особенной функции 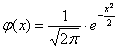 мы поговорим на уроке о нормальном распределении вероятностей, а пока нам потребуется формально-вычислительная сторона вопроса. В частности, важным фактом является чётность этой функции:
мы поговорим на уроке о нормальном распределении вероятностей, а пока нам потребуется формально-вычислительная сторона вопроса. В частности, важным фактом является чётность этой функции: 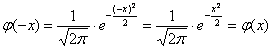 .
.
Числовые характеристики.
На практике часто ограничиваются рассмотрением хотя и менее полных, но зато более простых характеристик случайных величин (процессов), называемых числовыми характеристиками или моментами. Числовой характеристикой случайной величины может служить момент  порядка, определяемый как
порядка, определяемый как
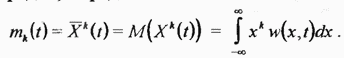
В частности, момент первого порядка, называемый математическим ожиданием  определяет среднее значение случайной величины
определяет среднее значение случайной величины
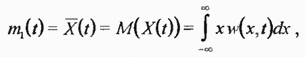
где черта сверху означает усреднение по множеству реализаций. Аналогично вводится момент второго порядка

Разность между случайной величиной X и её  представляет собой отклонение
представляет собой отклонение  от среднего значения. Она называется центрированным значением
от среднего значения. Она называется центрированным значением  квадрата этого отклонения называется дисперсией или центральным моментом второго порядка
квадрата этого отклонения называется дисперсией или центральным моментом второго порядка
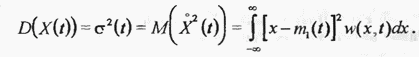
Величину  называют стандартным или среднеквадратическим отклонением. С учётом (2.65) и (2.66) выражение (2.67) приводится к результату
называют стандартным или среднеквадратическим отклонением. С учётом (2.65) и (2.66) выражение (2.67) приводится к результату
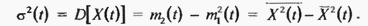
Дисперсия характеризует разброс случайной величины относительно её среднего значения.  и дисперсия
и дисперсия  являются важными характеристиками случайной величины, однако они не дают достаточного представления о изменчивости случайного процесса во времени. При совместном изучении центрированных случайных величин
являются важными характеристиками случайной величины, однако они не дают достаточного представления о изменчивости случайного процесса во времени. При совместном изучении центрированных случайных величин  сечений
сечений  центрированного случайного процесса
центрированного случайного процесса  вводится понятие смешанного момента второго порядка, называемого функцией корреляции
вводится понятие смешанного момента второго порядка, называемого функцией корреляции 
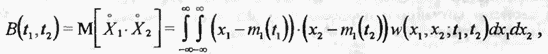
где  двумерная плотность вероятности. Функция корреляции характеризует степень статистической взаимосвязи значений
двумерная плотность вероятности. Функция корреляции характеризует степень статистической взаимосвязи значений  случайного процесса
случайного процесса  в моменты
в моменты  разделённые интервалом
разделённые интервалом  (см. рис. 2.15). Убывание ФК с увеличением
(см. рис. 2.15). Убывание ФК с увеличением  свидетельствует об ослаблении связи между мгновенными значениями процесса. Если ФК при каких-либо значениях
свидетельствует об ослаблении связи между мгновенными значениями процесса. Если ФК при каких-либо значениях  имеет отрицательное значение, это свидетельствует о том, что положительным отклонениям процесса в одном сечении соответствуют преимущественно отрицательные отклонения в другом сечении и наоборот. Если случайные величины
имеет отрицательное значение, это свидетельствует о том, что положительным отклонениям процесса в одном сечении соответствуют преимущественно отрицательные отклонения в другом сечении и наоборот. Если случайные величины  и
и  статистически независимы, то их двумерные ПВ определяется произведением одномерных
статистически независимы, то их двумерные ПВ определяется произведением одномерных  между двумя такими сечениями, как следует из (2.68), равна нулю.
между двумя такими сечениями, как следует из (2.68), равна нулю.
Плотность распределения
Пусть имеется непрерывная случайная величина  с функцией распределения
с функцией распределения 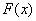 , которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от
, которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от  до
до 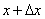 :
:
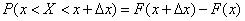 ,
,
т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать 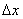 к нулю. В пределе получим производную от функции распределения:
к нулю. В пределе получим производную от функции распределения:
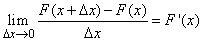 . (5.4.1)
. (5.4.1)
Введем обозначение:
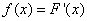 . (5.4.2)
. (5.4.2)
Функция  - производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины
- производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины  .
.
Термины «плотность распределения», «плотность вероятности» становятся особенно наглядными при пользовании механической интерпретацией распределения; в этой интерпретации функция  буквально характеризует плотность распределения масс по оси абсцисс (так называемую «линейную плотность»). Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 5.4.1).
буквально характеризует плотность распределения масс по оси абсцисс (так называемую «линейную плотность»). Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 5.4.1).
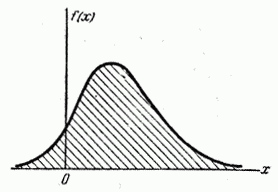
Рис. 5.4.1.
Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.
Рассмотрим непрерывную случайную величину  с плотностью распределения
с плотностью распределения  и элементарный участок
и элементарный участок 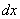 , примыкающий к точке
, примыкающий к точке  (рис. 5.4.2). Вероятность попадания случайной величины
(рис. 5.4.2). Вероятность попадания случайной величины  на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна
на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна  . Величина
. Величина  называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок
называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок 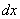 (рис. 5.4.2).
(рис. 5.4.2).
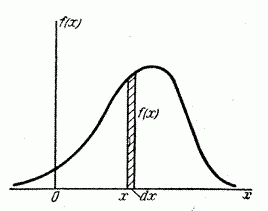
Рис. 5.4.2.
Выразим вероятность попадания величины  на отрезок от
на отрезок от 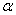 до
до 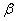 (рис 5.4.3) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т.е. интегралу:
(рис 5.4.3) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т.е. интегралу:
 (5.4.3)
(5.4.3)
*) Так как вероятность любого отдельного значения непрерывной случайной величины равна нулю, то можно рассматривать здесь отрезок 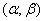 , не включая в него левый конец, т.е. отбрасывая знак равенства в
, не включая в него левый конец, т.е. отбрасывая знак равенства в  .
.
Геометрически вероятность попадания величины  на участок
на участок 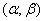 равна площади кривой распределения, опирающейся на этот участок (рис. 5.4.3.).
равна площади кривой распределения, опирающейся на этот участок (рис. 5.4.3.).
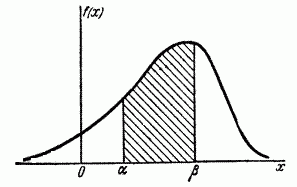
Рис. 5.4.3.
Формула (5.4.2.) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению
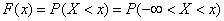 ,
,
откуда по формуле (5.4.3) имеем:
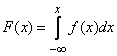 . (5.4.4)
. (5.4.4)
Геометрически 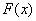 есть не что иное, как площадь кривой распределения, лежащая левее точки
есть не что иное, как площадь кривой распределения, лежащая левее точки  (рис. 5.4.4).
(рис. 5.4.4).
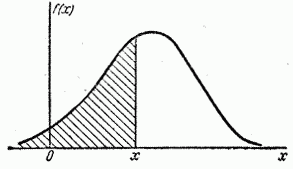
Рис. 5.4.4.
Укажем основные свойства плотности распределения.
1. Плотность распределения есть неотрицательная функция:
 .
.
Это свойство непосредственно вытекает из того, что функция распределения 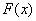 есть неубывающая функция.
есть неубывающая функция.
2. Интеграл в бесконечных пределах от плотности распределения равен единице:
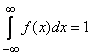 .
.
Это следует из формулы (5.4.4) и из того, что 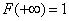 .
.
Геометрически основные свойства плотности распределения означают, что:
1) вся кривая распределения лежит не ниже оси абсцисс;
2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Выясним размерность основных характеристик случайной величины – функции распределения и плотности распределения. Функция распределения 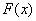 , как всякая вероятность, есть величина безразмерная. Размерность плотности распределения
, как всякая вероятность, есть величина безразмерная. Размерность плотности распределения  , как видно из формулы (5.4.1), обратна размерности случайной величины.
, как видно из формулы (5.4.1), обратна размерности случайной величины.
Пример 1. Функция распределения непрерывной случайной величины Х задана выражением
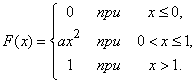
а) Найти коэффициент а.
б) Найти плотность распределения  .
.
в) Найти вероятность попадания величины  на участок от 0,25 до 0,5.
на участок от 0,25 до 0,5.
Решение. а) Так как функция распределения величины  непрерывна, то при
непрерывна, то при 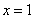
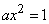 , откуда
, откуда 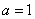 .
.
б) Плотность распределения величины  выражается формулой
выражается формулой
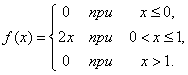
в) По формуле (5.3.1) имеем:
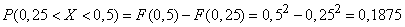 .
.
Пример 2. Случайная величина  подчинена закону распределения с плотностью:
подчинена закону распределения с плотностью:
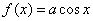 при
при 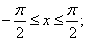
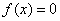 при
при  или
или  .
.
а) Найти коэффициент а.
б) Построить график плотности распределения  .
.
в) Найти функцию распределения 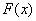 и построить её график.
и построить её график.
г) Найти вероятность попадания величины  на участок от 0 до
на участок от 0 до 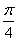 .
.
Решение. а) Для определения коэффициента а воспользуемся свойством плотности распределения:
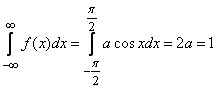 ,
,
откуда 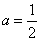 .
.
б) График плотности  представлен на рис. 5.4.5.
представлен на рис. 5.4.5.
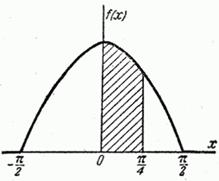
Рис. 5.4.5.
в) По формуле (5.4.4) получаем выражение функции распределения:
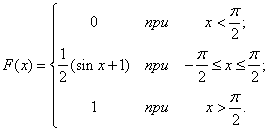
График функции 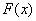 изображен на рис. 5.4.6.
изображен на рис. 5.4.6.

Рис. 5.4.6.
г) По формуле (5.3.1) имеем:
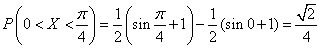 .
.
Тот же результат, но несколько более сложным путем, можно получить по формуле (5.4.3).
Пример 3. Плотность распределения случайной величины  задана формулой:
задана формулой:
 .
.
а) Построить график плотности  .
.
б) Найти вероятность того, что величина  попадет на участок (-1, +1).
попадет на участок (-1, +1).
Решение. а) График плотности дан на рис. 5.4.7.
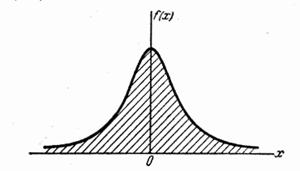
Рис. 5.4.7.
б) По формуле (5.4.3) имеем:
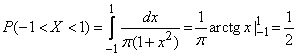 .
.
14. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ (гауссово) (или распределение нормальной случайной величины  ) — распределение вероятностей, задаваемое дифференциальным законом (функцией):
) — распределение вероятностей, задаваемое дифференциальным законом (функцией):
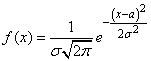 ,
,
здесь  — математическое ожидание случайной величины
— математическое ожидание случайной величины  ,
,  — среднеквадратическое отклонение
— среднеквадратическое отклонение  ,
,  — плотность вероятности случайной величины
— плотность вероятности случайной величины  в точке
в точке  . Графики функций
. Графики функций  при различных
при различных  ,
,  приведены на рисунке 21. Рисунок иллюстрирует зависимость кривых
приведены на рисунке 21. Рисунок иллюстрирует зависимость кривых  от
от 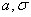 : вершина кривой имеет абсциссу
: вершина кривой имеет абсциссу 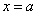 , кривая симметрична относительно прямой
, кривая симметрична относительно прямой 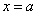 , большему
, большему  соответствует пологая кривая, малому
соответствует пологая кривая, малому  — островершинная, крутая кривая; точки перегиба кривой имеют абсциссы
— островершинная, крутая кривая; точки перегиба кривой имеют абсциссы 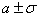 . Площадь под каждой из кривых равна 1.
. Площадь под каждой из кривых равна 1.

Рис. 21
Дифференциальная функция  , задающая, нормальную случайную величину
, задающая, нормальную случайную величину  , позволяет вычислить вероятности
, позволяет вычислить вероятности 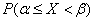 того, что случайная величина
того, что случайная величина  примет свое значение в интервале
примет свое значение в интервале  :
:
 . (*)
. (*)
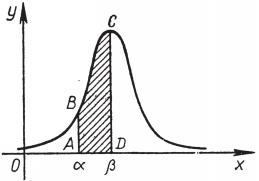
Рис. 22
Формула (*) может быть истолкована в геометрических терминах: вероятность 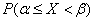 численно равна площади криволинейной трапеции
численно равна площади криволинейной трапеции  (рис. 22). Поскольку первообразная функции
(рис. 22). Поскольку первообразная функции  не является элементарной функцией, вычисление интегралов (*) производят с помощью таблиц функции
не является элементарной функцией, вычисление интегралов (*) производят с помощью таблиц функции
 ,
,
называемой Лапласа функцией. Именно:
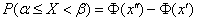 ,
,  ,
,  .
.
Легко вычислить, что
 ,
,
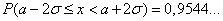 ,
,
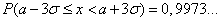 .
.
Эти соотношения называют правилами одной, двух и трех сигм соответственно. Последняя формула означает, что событие 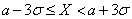 почти всегда наступает (
почти всегда наступает (  ). Такое событие называют практически достоверным событием.
). Такое событие называют практически достоверным событием.
Н. р., а также нормальная случайная величина называются также распределением Гаусса и гауссовой случайной величиной.
Н. р. играет исключительно важную роль в теории вероятности и математической статистике. Причиной этому являются те общие свойства случайных величин, которые формируются в предельных теоремах теории вероятностей и, в особенности, в центральной предельной теореме А. М. Ляпунова. Согласно этой теореме всякая случайная величина  , равная сумме большого количества «мелких» независимых случайных величин, имеет распределение, близкое к Н. р. При этом на практике часто встречаются случайные величины
, равная сумме большого количества «мелких» независимых случайных величин, имеет распределение, близкое к Н. р. При этом на практике часто встречаются случайные величины  с указанным выше свойством, что позволяет считать распределение случайной величины
с указанным выше свойством, что позволяет считать распределение случайной величины  близким к Н. р.
близким к Н. р.
Совместное распределение нескольких случайных величин называется многомерным Н. р., если дифференциальный закон этого распределения имеет вид:
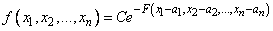 ,
,
где  ,
, 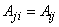 — положительно определенная квадратическая форма.
— положительно определенная квадратическая форма.
Постоянная 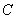 такова, что интеграл
такова, что интеграл 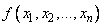 по всему пространству равняется единице. Числа
по всему пространству равняется единице. Числа 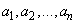 являются математическими ожиданиями случайных величин
являются математическими ожиданиями случайных величин  соответственно, а коэффициент
соответственно, а коэффициент 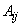 выражается через дисперсии
выражается через дисперсии 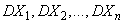 этих величин и через коэффициенты корреляции
этих величин и через коэффициенты корреляции 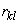 величин
величин 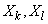 ;
;  .
.
Равномерное распределение.
Наиболее простым является равномерное распределение (рис. 2.17), для которого плотность вероятност и постоянна для данного интервала  и равна нулю за его пределами, т.е.
и равна нулю за его пределами, т.е.
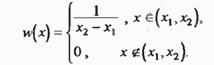
Если, например, измерение какой-либо величины производится с точностью до целого числа делений шкалы измерительного прибора, так что ошибки, превосходящие по абсолютному значению половину деления (или половину тага квантования в приборах с цифровым

Рис. 2.17. Плотность вероятности при равномерном распределении
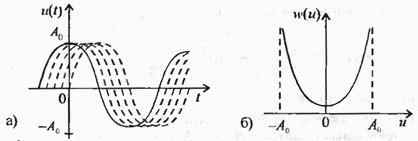
Рис. 2.18 Гармонический сигнал со случайной фазой, его (а) реализация и (б) плотность вероятности
отсчётом), практически невозможны, то ошибка измерений 8 представляет собой равномерно распределённую  Возможными значениями
Возможными значениями  являются в этом смысле действительные числа, не превосходящие по абсолютной величине половину деления шкалы.
являются в этом смысле действительные числа, не превосходящие по абсолютной величине половину деления шкалы.
Классическими примерами, связанными с Н. р., являются задача о броуновском движении, задача о распределении ошибок наблюдения (К. Ф. Гаусс), задача о распределении скоростей молекул (Дж. К. Максвелл).
Закон Пуассона
Во многих задачах практики приходится иметь дело со случайными величинами, распределенными по своеобразному закону, который называется законом Пуассона.
Рассмотрим прерывную случайную величину  , которая может принимать только целые, неотрицательные значения:
, которая может принимать только целые, неотрицательные значения:
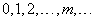 ,
,
причем последовательность этих значений теоретически не ограничена.
Говорят, что случайная величина  распределена по закону Пуассона, если вероятность того, что она примет определенное значение
распределена по закону Пуассона, если вероятность того, что она примет определенное значение 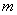 , выражается формулой
, выражается формулой
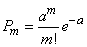
 , (5.9.1)
, (5.9.1)
где а – некоторая положительная величина, называемая параметром закона Пуассона.
Ряд распределения случайной величины  , распределенной по закону Пуассона, имеет вид:
, распределенной по закону Пуассона, имеет вид:
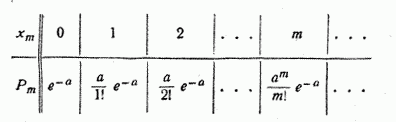
Убедимся, прежде всего, что последовательность вероятностей, задаваемая формулой (5.9.1), может представлять собой ряд распределения, т.е. что сумма всех вероятностей  равна единице. Имеем:
равна единице. Имеем:
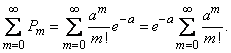
Но
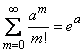 ,
,
откуда
 .
.
На рис. 5.9.1 показаны многоугольники распределения случайной величины  , распределенной по закону Пуассона, соответствующие различным значениям параметра
, распределенной по закону Пуассона, соответствующие различным значениям параметра  . В таблице 8 приложения приведены значения
. В таблице 8 приложения приведены значения  для различных
для различных  .
.

Рис. 5.9.1.
Определим основные характеристики – математическое ожидание и дисперсию – случайной величины  , распределенной по закону Пуассона. По определению математического ожидания
, распределенной по закону Пуассона. По определению математического ожидания
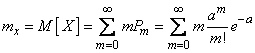 .
.
Первый член суммы (соответствующий  ) равен нулю, следовательно, суммирование можно начать с
) равен нулю, следовательно, суммирование можно начать с 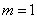 :
:
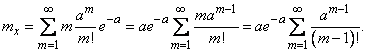
Обозначим 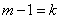 ; тогда
; тогда
 . (5.9.2)
. (5.9.2)
Таким образом, параметр  представляет собой не что иное, как математическое ожидание случайной величины
представляет собой не что иное, как математическое ожидание случайной величины  .
.
Для определения дисперсии найдем сначала второй начальный момент величины  :
:

По ранее доказанному
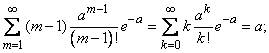
кроме того,

следовательно,

Далее находим дисперсию величины  :
:
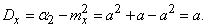 (5.9.3)
(5.9.3)
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна её математическому ожиданию  .
.
Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина  распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
Определим для случайной величины  , распределенной по закону Пуассона, вероятность того, что она примет значение не меньше заданного
, распределенной по закону Пуассона, вероятность того, что она примет значение не меньше заданного 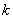 . Обозначим эту вероятность
. Обозначим эту вероятность 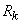 :
:
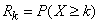 .
.
Очевидно, вероятность 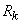 может быть вычислена как сумма
может быть вычислена как сумма

Однако значительно проще определить её из вероятности противоположного события:
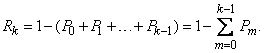 (5.9.4)
(5.9.4)
В частности, вероятность того, что величина  примет положительное значение, выражается формулой
примет положительное значение, выражается формулой
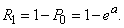 (5.9.5)
(5.9.5)
Мы уже упоминали о том, что многие задачи практики приводят к распределению Пуассона. Рассмотрим одну из типичных задач такого рода.

Рис. 5.9.2.
Пусть на оси абсцисс Ох случайным образом распределяются точки (рис. 5.9.2). Допустим, что случайное распределение точек удовлетворяет следующим условиям:
1. Вероятность попадания того или иного числа точек на отрезок  зависит только от длины этого отрезка, но не зависит от его положения на оси абсцисс. Иными словами, точки распределяются на оси абсцисс с одинаковой средней плотностью. Обозначим эту плотность (т.е. математическое ожидание числа точек, приходящихся на единицу длины) через
зависит только от длины этого отрезка, но не зависит от его положения на оси абсцисс. Иными словами, точки распределяются на оси абсцисс с одинаковой средней плотностью. Обозначим эту плотность (т.е. математическое ожидание числа точек, приходящихся на единицу длины) через 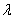 .
.
2. Точки распределяются на оси абсцисс независимо друг от друга, т.е. вероятность попадания того или другого числа точек на заданный отрезок не зависит от того, сколько их попало на любой другой отрезок, не перекрывающийся с ним.
3. Вероятность попадания на малый участок 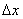 двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек).
двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек).
Выделим на оси абсцисс определенный отрезок длины  и рассмотрим дискретную случайную величину
и рассмотрим дискретную случайную величину  – число точек, попадающих на этот отрезок. Возможные значения величины будут
– число точек, попадающих на этот отрезок. Возможные значения величины будут
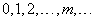 (5.9.6)
(5.9.6)
Так как точки попадают на отрезок независимо друг от друга, то теоретически не исключено, что их там окажется сколь угодно много, т.е. ряд (5.9.6) продолжается неограниченно.
Докажем, что случайная величина  имеет закон распределения Пуассона. Для этого вычислим вероятность
имеет закон распределения Пуассона. Для этого вычислим вероятность  того, что на отрезок
того, что на отрезок  попадет ровно
попадет ровно 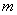 точек.
точек.
Сначала решим более простую задачу. Рассмотрим на оси Ох малый участок 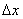 и вычислим вероятность того, что на этот участок попадет хотя бы одна точка. Будем рассуждать следующим образом. Математическое ожиданиечисла точек, попадающих на этот участок, очевидно, равно
и вычислим вероятность того, что на этот участок попадет хотя бы одна точка. Будем рассуждать следующим образом. Математическое ожиданиечисла точек, попадающих на этот участок, очевидно, равно 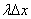 (т.к. на единицу длины попадает в среднем
(т.к. на единицу длины попадает в среднем 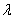 точек). Согласно условию 3 для малого отрезка
точек). Согласно условию 3 для малого отрезка 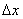 можно пренебречь возможностью попадания на него двух или больше точек. Поэтому математическое ожидание
можно пренебречь возможностью попадания на него двух или больше точек. Поэтому математическое ожидание 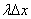 числа точек, попадающих на участок
числа точек, попадающих на участок 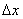 , будет приближенно равно вероятности попадания на него одной точки (или, что в наших условиях равнозначно, хотя бы одной).
, будет приближенно равно вероятности попадания на него одной точки (или, что в наших условиях равнозначно, хотя бы одной).
Таким образом, с точностью до бесконечно малых высшего порядка, при  можно считать вероятность того, что на участок
можно считать вероятность того, что на участок 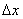 попадет одна (хотя бы одна) точка, равной
попадет одна (хотя бы одна) точка, равной 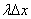 , а вероятность того, что не попадет ни одной, равной
, а вероятность того, что не попадет ни одной, равной 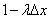 .
.
Воспользуемся этим для вычисления вероятности  попадания на отрезок
попадания на отрезок  ровно
ровно 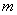 точек. Разделим отрезок
точек. Разделим отрезок  на
на  равных частей длиной
равных частей длиной 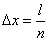 . Условимся называть элементарный отрезок
. Условимся называть элементарный отрезок 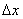 «пустым», если в него не попало ни одной точки, и «занятым», если в него попала хотя бы одна. Согласно выше доказанному вероятность того, что отрезок
«пустым», если в него не попало ни одной точки, и «занятым», если в него попала хотя бы одна. Согласно выше доказанному вероятность того, что отрезок 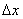 окажется «занятым», приближенно равна
окажется «занятым», приближенно равна  ; вероятность того, что он окажется «пустым», равна
; вероятность того, что он окажется «пустым», равна 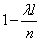 . Так как, согласно условию 2, попадания точек в неперекрывающиеся отрезки независимы, то наши n отрезков можно рассмотреть как
. Так как, согласно условию 2, попадания точек в неперекрывающиеся отрезки независимы, то наши n отрезков можно рассмотреть как  независимых «опытов», в каждом из которых отрезок может быть «занят» с вероятностью
независимых «опытов», в каждом из которых отрезок может быть «занят» с вероятностью  . Найдем вероятность того, что среди
. Найдем вероятность того, что среди  отрезков будет ровно
отрезков будет ровно 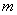 «занятых». По теореме о повторении опытов эта вероятность равна
«занятых». По теореме о повторении опытов эта вероятность равна
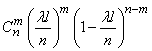
или, обозначая 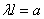 ,
,
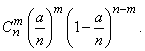 (5.9.7)
(5.9.7)
При достаточно большом  эта вероятность приближенно равна вероятности попадания на отрезок
эта вероятность приближенно равна вероятности попадания на отрезок  ровно
ровно 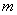 точек, так как попадание двух или больше точек на отрезок
точек, так как попадание двух или больше точек на отрезок 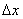 имеет пренебрежимо малую вероятность. Для того чтобы найти точное значение
имеет пренебрежимо малую вероятность. Для того чтобы найти точное значение  , нужно в выражении (5.9.7) перейти к пределу при
, нужно в выражении (5.9.7) перейти к пределу при 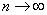 :
:
 (5.9.8)
(5.9.8)
Преобразуем выражение, стоящее под знаком предела:
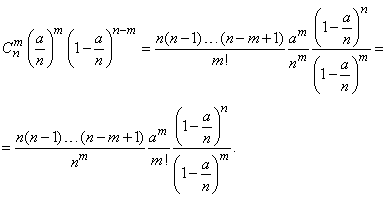 (5.9.9)
(5.9.9)
Первая дробь и знаменатель последней дроби в выражении (5.9.9) при 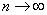 , очевидно, стремятся к единице. Выражение
, очевидно, стремятся к единице. Выражение 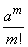 от
от  не зависит. Числитель последней дроби можно преобразовать так:
не зависит. Числитель последней дроби можно преобразовать так:
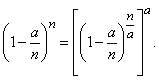 (5.9.10)
(5.9.10)
При 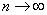
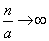 и выражение (5.9.10) стремится к
и выражение (5.9.10) стремится к 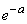 . Таким образом, доказано, что вероятность попадания ровно
. Таким образом, доказано, что вероятность попадания ровно 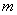 точек в отрезок
точек в отрезок  выражается формулой
выражается формулой
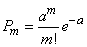 ,
,
где 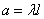 , т.е. величина Х распределена по закону Пуассона с параметром
, т.е. величина Х распределена по закону Пуассона с параметром 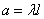 .
.
Отметим, что величина  по смыслу представляет собой среднее число точек, приходящееся на отрезок
по смыслу представляет собой среднее число точек, приходящееся на отрезок  .
.
Величина 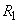 (вероятность того, что величина Х примет положительное значение) в данном случае выражает вероятность того, что на отрезок
(вероятность того, что величина Х примет положительное значение) в данном случае выражает вероятность того, что на отрезок  попадет хотя бы одна точка:
попадет хотя бы одна точка:
 . (5.9.11)
. (5.9.11)
Таким образом, мы убедились, что распределение Пуассона возникает там, где какие-то точки (или другие элементы) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек, попавших в какую-то область. В нашем случае такой «областью» был отрезок  на оси абсцисс. Однако наш вывод легко распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
на оси абсцисс. Однако наш вывод легко распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
1) точки распределены в поле статистически равномерно со средней плотностью 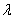 ;
;
2) точки попадают в неперекрывающиеся области независимым образом;
3) точки появляются поодиночке, а не парами, тройками и т.д., то число точек  , попадающих в любую область
, попадающих в любую область 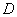 (плоскую или пространственную), распределяются по закону Пуассона:
(плоскую или пространственную), распределяются по закону Пуассона:
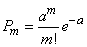
 ,
,
где  – среднее число точек, попадающих в область
– среднее число точек, попадающих в область 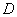 .
.
Для плоского случая
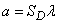 ,
,
где 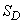 – площадь области
– площадь области 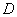 ; для пространственного
; для пространственного
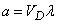 ,
,
где 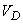 - объем области
- объем области 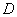 .
.
Заметим, что для пуассоновского распределения числа точек, попадающих в отрезок или область, условие постоянной плотности ( 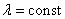 ) несущественно. Если выполнены два других условия, то закон Пуассона все равно имеет место, только параметр а в нем приобретает другое выражение: он получается не простым умножение плотности
) несущественно. Если выполнены два других условия, то закон Пуассона все равно имеет место, только параметр а в нем приобретает другое выражение: он получается не простым умножение плотности 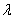 на длину, площадь или объем области, а интегрированием переменной плотности по отрезку, площади или объему. (Подробнее об этом см. n° 19.4)
на длину, площадь или объем области, а интегрированием переменной плотности по отрезку, площади или объему. (Подробнее об этом см. n° 19.4)
Наличие случайных точек, разбросанных на линии, на плоскости или объеме – неединственное условие, при котором возникает распределение Пуассона. Можно, например, доказать, что закон Пуассона является предельным для биномиального распределения:
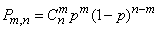 , (5.9.12)
, (5.9.12)
если одновременно устремлять число опытов  к бесконечности, а вероятность
к бесконечности, а вероятность 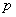 – к нулю, причем их произведение
– к нулю, причем их произведение 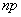 сохраняет постоянное значение:
сохраняет постоянное значение:
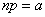 . (5.9.13)
. (5.9.13)
Действительно, это предельное свойство биномиального распределения можно записать в виде:
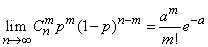 . (5.9.14)
. (5.9.14)
Но из условия (5.9.13) следует, что
 . (5.9.15)
. (5.9.15)
Подставляя (5.9.15) в (5.9.14), получим равенство
 , (5.9.16)
, (5.9.16)
которое только что было доказано нами по другому поводу.
Это предельное свойство биномиального закона часто находит применение на практике. Допустим, что производится большое количество независимых опытов  , в каждом из которых событие
, в каждом из которых событие  имеет очень малуювероятность
имеет очень малуювероятность 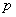 . Тогда для вычисления вероятности
. Тогда для вычисления вероятности 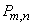 того, что событие
того, что событие  появится ровно
появится ровно 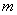 раз, можно воспользоваться приближенной формулой:
раз, можно воспользоваться приближенной формулой:
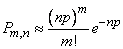 , (5.9.17)
, (5.9.17)
где 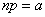 - параметр того закона Пуассона, которым приближенно заменяется биномиальное распределение.
- параметр того закона Пуассона, которым приближенно заменяется биномиальное распределение.
От этого свойства закона Пуассона – выражать биномиальное распределение при большом числе опытов и малой вероятности события – происходит его название, часто применяемое в учебниках статистики: закон редких явлений.
Рассмотрим несколько примеров, связанных с пуассоновским распределением, из различных областей практики.
Распределение статистики
Теперь вернемся к тому, что, вероятно, представляет наиболее трудную проблему для начинающего изучать математическую статистику: к понятию распределения статистики (или статистических параметров, таких как среднее значение или дисперсия выборки).
Предположим, что мы сделали ряд измерений и что по этой выборке вычислили одну или несколько статистик. Например, мы можем случайным образом выбрать 1000 американцев из общего населения около 200 миллионов и измерить рост каждого. Исходя из полученных данных, можно вычислить среднее значение выборки х. Дисперсия  выборки определяется следующим образом:
выборки определяется следующим образом:

Для ясности, обычно используют греческие буквы для обозначения статистик модели и латинские буквы для соответствующей статистики выборки.
Хорошо бы знать указанные два числа для выборки, которую мы взяли. Однако, если от этих чиеел ждут большой пользы, то сразу же возникает вопрос: что разумного можно получить для уточнения среднего значения, если весь процесс повторить снова, используя
Таблица 1.6.1. (см. скан)
Связь статистик выборки и множества
разную случайную выборку 1000 американцев? Короче говоря, что такое «среднее» распределения статистики? Очевидно, повторение всего процесса выбора людей, проведение измерений и вычисление среднего даст нам распределение величин среднего значения х (и распределение дисперсии 
В примере с округлением имелась уникальная модель для исходного множества чисел, из которого извлекались округленные значения, а в примере с гауссовым распределением достаточно оценить два неизвестных параметра множества: распределение  по статистикам выборки
по статистикам выборки  Можно поинтересоваться, какая существует связь между этими парами чисел (табл. 1.6.1). В руководствах по статистике доказывается, что для любого распределения среднее выборки есть несмещенная оценка среднего значения исходной совокупности. Аналогично дисперсия выборки
Можно поинтересоваться, какая существует связь между этими парами чисел (табл. 1.6.1). В руководствах по статистике доказывается, что для любого распределения среднее выборки есть несмещенная оценка среднего значения исходной совокупности. Аналогично дисперсия выборки  определяется несмещенной оценкой
определяется несмещенной оценкой  Несмещенная оценка означает, что в среднем оценки не слишком велики и не слишком малы, т. е. среднее значение статистики равно той величине, которая оценивается.
Несмещенная оценка означает, что в среднем оценки не слишком велики и не слишком малы, т. е. среднее значение статистики равно той величине, которая оценивается.
Если выборка достаточно велика  тогда центральная предельная теорема утверждает, что статистика, называемая средним значением, имеет распределение, очень близкое к гауссовому (нормальному) распределению
тогда центральная предельная теорема утверждает, что статистика, называемая средним значением, имеет распределение, очень близкое к гауссовому (нормальному) распределению
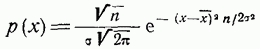
с параметрами 
ОБРАБОТКА ОПЫТОВ
В главе 7 мы уже рассмотрели некоторые задачи математической статистики, относящиеся к обработке опытных данных. Это были главным образом задачи о нахождении законов распределения случайных величии по результатам опытов. Чтобы найти закон распределения, нужно располагать достаточно обширным статистическим материалом, порядка нескольких сотен опытов (наблюдений). Однако на практике часто приходится иметь дело со статистическим материалом весьма ограниченного объема - с двумя-тремя десятками наблюдении, часто даже меньше. Это обычно связано с дороговизной и сложностью постановки каждого опыта. Такого ограниченного материала явно недостаточно для того, чтобы найти заранее неизвестный закон распределения случайной величины; но все же этот материал может быть обработан и использован для получения некоторых сведений о случайной величине. Например, на основе ограниченного статистического материала можно определить - хотя бы ориентировочно - важнейшие числовые характеристики случайной величины: математическое ожидание, дисперсию, иногда - высшие моменты. На практике часто бывает, что вид закона распределения известен заранее, а требуется найти только некоторые параметры, от которых он зависит. Например, если заранее известно, что закон распределения случайной величины нормальный, то задача обработки сводится к определению двух его параметров 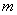 и
и  . Если заранее известно, что величина распределена по закону Пуассона, то подлежит определению только один его параметр: математическое ожидание
. Если заранее известно, что величина распределена по закону Пуассона, то подлежит определению только один его параметр: математическое ожидание  . Наконец, в некоторых задачах вид закона распределения вообще несуществен, а требуется знать только его числовые характеристики.
. Наконец, в некоторых задачах вид закона распределения вообще несуществен, а требуется знать только его числовые характеристики.
В данной главе мы рассмотрим ряд задач об определении неизвестных параметров, от которых зависит закон распределения случайной величины, но ограниченному числу опытов.
Прежде всего нужно отметить, что любое значение искомого параметра, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайности. Такое приближенное, случайное значение мы будем называть оценкой параметра. Например, оценкой для математического ожидания может служить среднее арифметическое наблюденных значений случайной величины в  независимых опытах. При очень большом числе опытов среднее арифметическое будет с большой вероятностью весьма близко к математическому ожиданию. Если же число опытов
независимых опытах. При очень большом числе опытов среднее арифметическое будет с большой вероятностью весьма близко к математическому ожиданию. Если же число опытов  невелико, то замена математического ожидания средним арифметическим приводит к какой-то ошибке. Эта ошибка в среднем тем больше, чем меньше число опытов. Так же будет обстоять дело и с оценками других неизвестных параметров. Любая из таких оценок случайна; при пользовании ею неизбежны ошибки. Желательно выбрать такую оценку, чтобы эти ошибки были по возможности минимальными.
невелико, то замена математического ожидания средним арифметическим приводит к какой-то ошибке. Эта ошибка в среднем тем больше, чем меньше число опытов. Так же будет обстоять дело и с оценками других неизвестных параметров. Любая из таких оценок случайна; при пользовании ею неизбежны ошибки. Желательно выбрать такую оценку, чтобы эти ошибки были по возможности минимальными.
Рассмотрим следующую общую задачу. Имеется случайная величина  , закон распределения которой содержит неизвестный параметр
, закон распределения которой содержит неизвестный параметр  . Требуется найти подходящую оценку для параметра
. Требуется найти подходящую оценку для параметра  по результатам
по результатам  независимых опытов, в каждом из которых величина
независимых опытов, в каждом из которых величина  приняла определенное значение.
приняла определенное значение.
Обозначим наблюденные значения случайной величины
 . (14.1.1)
. (14.1.1)
Их можно рассматривать как  «экземпляров» случайной величины
«экземпляров» случайной величины  , то есть
, то есть  независимых случайных величин, каждая из которых распределена по тому же закону, что и случайная величина
независимых случайных величин, каждая из которых распределена по тому же закону, что и случайная величина  .
.
Обозначим  оценку для параметра
оценку для параметра  . Любая оценка, вычисляемая на основе материала (14.1.1), должна представлять собой функцию величин
. Любая оценка, вычисляемая на основе материала (14.1.1), должна представлять собой функцию величин  :
:
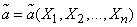 (14.1.2)
(14.1.2)
и, следовательно, сама является величиной случайной. Закон распределения  зависит, во-первых, от закона распределения величины
зависит, во-первых, от закона распределения величины  (и, в частности, от самого неизвестного параметра
(и, в частности, от самого неизвестного параметра  ); во-вторых, от числа опытов
); во-вторых, от числа опытов  . В принципе этот закон распределения может быть найден известными методами теории вероятностей.
. В принципе этот закон распределения может быть найден известными методами теории вероятностей.
Предъявим к оценке  ряд требований, которым она должна удовлетворять, чтобы быть в каком-то смысле «доброкачественной» оценкой.
ряд требований, которым она должна удовлетворять, чтобы быть в каком-то смысле «доброкачественной» оценкой.
Естественно потребовать от оценки  , чтобы при увеличении числа опытов
, чтобы при увеличении числа опытов  она приближалась (сходилась повероятности) к параметру
она приближалась (сходилась повероятности) к параметру  . Оценка, обладающая таким свойством, называется состоятельной.
. Оценка, обладающая таким свойством, называется состоятельной.
Кроме того, желательно, чтобы, пользуясь величиной  вместо
вместо  , мы по крайней мере не делали систематической ошибки в сторону завышения или занижения, т. е. чтобы выполнялось условие
, мы по крайней мере не делали систематической ошибки в сторону завышения или занижения, т. е. чтобы выполнялось условие
 . (14.1.3)
. (14.1.3)
Оценка, удовлетворяющая такому условию, называется несмещенной.
Наконец, желательно, чтобы выбранная несмещенная оценка обладала по сравнению с другими наименьшейдисперсией, т. е.
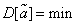 . (14.1.4)
. (14.1.4)
Оценка, обладающая таким свойством, называется эффективной.
На практике не всегда удается удовлетворить всем этим требованиям. Например, может оказаться, что, даже еслиэффективная оценка существует, формулы для ее вычисления оказываются слишком сложными, и приходится удовлетворяться другой оценкой, дисперсия которой несколько больше. Иногда применяются - в интересах простоты расчетов - незначительно смещенные оценки. Однако выбору оценки всегда должно предшествовать ее критическое рассмотрение со всех перечисленных выше точек зрения.
Формула Байеса
Пусть событие  происходит одновременно с одним из
происходит одновременно с одним из  несовместных событий
несовместных событий 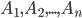 . Требуется найти вероятность события
. Требуется найти вероятность события  , если известно, что событие
, если известно, что событие  произошло.
произошло.
На основании теоремы о вероятности произведения двух событий можно написать
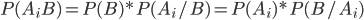
Откуда
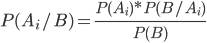
или
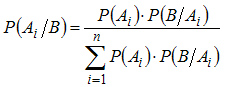 (3.2)
(3.2)
Формула (3.2) носит название формулы Байеса.
Пример. Три организации представили в контрольное управление счета для выборочной проверки. Первая организация представила 15 счетов, вторая — 10, третья — 25. Вероятности правильного оформления счетов у этих организаций известны и соответственно равны: 0,9; 0,8; 0,85. Был выбран один счет и он оказался правильным. Определить вероятность того, что этот счет принадлежит второй организации.
Решение. Пусть 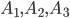 — события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут
— события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут
 ,
,  ,
, 
По формуле полной вероятности определяем вероятность выбора правильно оформленного счета

По формуле Байеса находим исходную вероятность
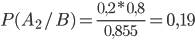
Повторение независимых испытаний. Формулы Бернулли, Лапласа и Пуассона
Рассмотрим ситуацию, в которой одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других.
Пусть некоторый опыт (испытание) повторяется n раз. Будем считать, что вероятность осуществления события A, связанного с данным опытом, при каждом повторении опыта остается неизменной и равна p (0<р<1). Тогда вероятность того, что событие A не осуществится, также будет неизменной и равной q = 1 – p. Такая последовательность проведения одного и того же опыта называется последовательностью (повторением) независимых испытаний.
Независимость понимается в том смысле, что вероятность осуществления события A в любом по номеру повторении опыта не зависит от результатов опыта при всех других повторениях. Найдем вероятность Pn(k) того, что событие A в n испытаниях произойдет k раз.
1. Формула Бернулли. Примеры применения формулы Бернулли
Вероятность того, что в серии из n независимых испытаний событие А наступит ровно k раз (безразлично в какой последовательности) находят по формуле Бернулли, если n является достаточно небольшим значением:
Pn(k) = Сnk pk qn-k, где Сnk = n! / k!(n-k)! – число сочетаний из n по k, р – вероятность события А, q – вероятность противоположного события Ā.
В различных задачах приходится находить следующие вероятности:
- вероятность того, что в n испытаниях событие А наступит менее m раз: Рn(k<m) = Рn(0)+ Рn(1)+…+Рn(m-1);
- вероятность того, что в n испытаниях событие А наступит более m раз: Рn(k>m) = Рn(m+1)+ Рn(m+2)+…+ Рn(n);
- вероятность того, что в n испытаниях событие А наступит не более m раз: Рn(k≤m) = Рn(0)+ Рn(1)+…+Рn(m);
- вероятность того, что в n испытаниях событие А наступит не менее m раз: Рn(k≥m) = Рn(m)+ Рn(m+1)+…+ Рn(n);
- вероятность того, что в n испытаниях событие А наступит не менее k1 и не более k2 раз: Рn(k1≤k≤k2) = Рn(k1)+…+Рn(k2).
Задача 1.
Монету подбрасывают 10 раз. Какова вероятность того, что при десятикратном подбрасывании монеты герб выпадет 3 раза?
Решение. Число испытаний n=10 невелико, поэтому вероятность можно вычислить непосредственно по формуле Бернулли:
P10(3) = С103 p3 q10-3, где С103 = 10! / 3!(10-3)! = 120, р=1/2, q=1-р=1/2.
P10(3) = 120*(1/2)3*(1/2)7=120*1/210=120/1024=15/128≈0,117
7. оставим теперь более общую задачу.
Рассмотрим последовательность n независимых испытаний в каждом из которых может произойти или не произойти некоторое событие А. При этом вероятность появления события в каждом испытании различна.
Обозначим через 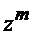
 . Аi – событие состоящее том что А произойдет в i-ом испытании
. Аi – событие состоящее том что А произойдет в i-ом испытании  – событие состоящее том что А не произойдет в i-ом испытании соответственно.
– событие состоящее том что А не произойдет в i-ом испытании соответственно.
Следует определить вероятность того что событие А произойдет m раз в серии из n испытаний.
Обозначим через Вm – событие состоящее в том что, событие А произойдет m раз в серии из n испытаний.

| (2.2.1) |
Здесь Аi – событие состоящее в том, что событие А произойдет в i- ом испытании. Событие Вmпредставляет собой сумму несовместных событий, поэтому
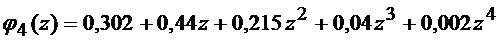
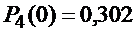
Число слагаемых в выражении равно  , но они все различные. Для вычисления
, но они все различные. Для вычисления 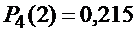 используют производящую функцию
используют производящую функцию
ProizFunc
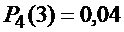
| (2.2.2) |
Зададимся целью найти в этом произведении коэффициент 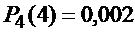 при
при  . Для этого перемножим биномы и произведем приведение подобных членов. Каждый член содержащий
. Для этого перемножим биномы и произведем приведение подобных членов. Каждый член содержащий  будет иметь в качестве коэффициента произведение m букв p с какими-то индексами и n-m букв q с другими оставшимися индексами, а после приведения подобных членов коэффициент при
будет иметь в качестве коэффициента произведение m букв p с какими-то индексами и n-m букв q с другими оставшимися индексами, а после приведения подобных членов коэффициент при  будет представлять собой сумму всех возможных произведений такого типа.
будет представлять собой сумму всех возможных произведений такого типа.
Таким образом, вероятность того, что событие А произойдет m раз в серии из n испытаний равна коэффициенту при  в выражении производящей функции, то есть
в выражении производящей функции, то есть
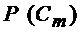
| (2.2.3) |

| (2.2.4) |
Если производятся n независимых опытов в различных условиях, причем вероятность появления события А в i-м опыте равна 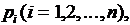 то вероятность Р
то вероятность Р 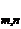 того, что событие А в n опытах появится m раз, равна коэффициенту при Z
того, что событие А в n опытах появится m раз, равна коэффициенту при Z 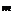 в разложении по степеням Z производящей функции
в разложении по степеням Z производящей функции  где
где 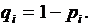
8 Данная статья является естественным продолжением урока о независимых испытаниях, на котором мы познакомились с формулой Бернулли и отработали типовые примеры по теме. Локальная и интегральная теоремы Лапласа (Муавра-Лапласа) решают аналогичную задачу с тем отличием, что они применимы к достаточно большому количеству независимых испытаний. Не нужно тушеваться слов «локальная», «интегральная», «теоремы» – материал осваивается с той же лёгкостью, с какой Лаплас потрепал кучерявую голову Наполеона. Поэтому безо всяких комплексов и предварительных замечаний сразу же рассмотрим демонстрационный пример:
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет 200 раз.
По характерным признакам здесь следует применить формулу Бернулли  . Вспомним смысл этих букв:
. Вспомним смысл этих букв:
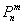 – вероятность того, что в
– вероятность того, что в  независимых испытаниях случайное событие
независимых испытаниях случайное событие  наступит ровно
наступит ровно 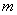 раз;
раз;
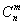 – биномиальный коэффициент;
– биномиальный коэффициент;
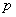 – вероятность появления события
– вероятность появления события  в каждом испытании;
в каждом испытании;
 – вероятность противоположного события.
– вероятность противоположного события.
Применительно к нашей задаче:
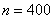 – общее количество испытаний;
– общее количество испытаний;
 – количество бросков, в которых должен выпасть орёл;
– количество бросков, в которых должен выпасть орёл;
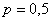 – вероятность выпадения орла в каждом броске;
– вероятность выпадения орла в каждом броске;
 – вероятность выпадения решки.
– вероятность выпадения решки.
Таким образом, вероятность того, что в результате 400 бросков монеты орёл выпадет ровно 200 раз: 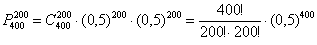 …Стоп, что делать дальше? Микрокалькулятор (по крайне мере, мой) не справился с 400-й степенью и капитулировал перед факториалами. А считать через произведение что-то не захотелось =) Воспользуемся стандартной функцией Экселя, которая сумела обработать монстра:
…Стоп, что делать дальше? Микрокалькулятор (по крайне мере, мой) не справился с 400-й степенью и капитулировал перед факториалами. А считать через произведение что-то не захотелось =) Воспользуемся стандартной функцией Экселя, которая сумела обработать монстра: 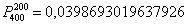 .
.
Заостряю ваше внимание, что получено точное значение и такое решение вроде бы идеально. На первый взгляд. Перечислим веские контраргументы:
– во-первых, программного обеспечения может не оказаться под рукой;
– и во-вторых, решение будет смотреться нестандартно (с немалой вероятностью придётся перерешивать);
Поэтому, уважаемые читатели, в ближайшем будущем нас ждёт:
Локальная теорема Лапласа
Если вероятность 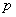 появления случайного события
появления случайного события  в каждом испытании постоянна, то вероятность
в каждом испытании постоянна, то вероятность 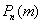 того, что в
того, что в  испытаниях событие
испытаниях событие  наступит ровно
наступит ровно 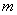 раз, приближённо равна:
раз, приближённо равна:
 , где
, где 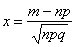 .
.
При этом, чем больше  , тем рассчитанная вероятность
, тем рассчитанная вероятность 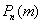 будет лучше приближать точное значению
будет лучше приближать точное значению 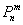 , полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат
, полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат 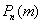 может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность
может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность 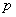 ближе к 0,5, и наоборот – даёт существенную погрешность при значениях
ближе к 0,5, и наоборот – даёт существенную погрешность при значениях 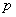 , близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы
, близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы  является выполнение неравенства
является выполнение неравенства 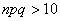 (
( 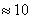 ).
).
Так, например, если  , то
, то 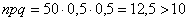 и применение теоремы Лапласа для 50 испытаний оправдано. Но если
и применение теоремы Лапласа для 50 испытаний оправдано. Но если 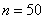 и
и 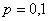 , то
, то 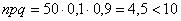 и приближение
и приближение 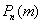 (к точному значению
(к точному значению 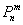 ) будет плохим.
) будет плохим.
О том, почему 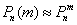 и об особенной функции
и об особенной функции 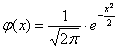 мы поговорим на уроке о нормальном распределении вероятностей, а пока нам потребуется формально-вычислительная сторона вопроса. В частности, важным фактом является чётность этой функции:
мы поговорим на уроке о нормальном распределении вероятностей, а пока нам потребуется формально-вычислительная сторона вопроса. В частности, важным фактом является чётность этой функции: 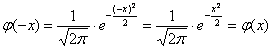 .
.
Дата: 2019-02-19, просмотров: 414.