В разделе 7.1 было сказано, что в подходящих случаях можно построить объективный критерий, позволяющий ответит на вопрос: совместима ли с данными используемая при их анализе вероятностная модель. Можно было бы ожидать, что каждый такой критерий, если он существует, должен быть специально «сконструирован» для каждого вида данных. Однако большинство критериев согласия, применяемых на практике, не имеет такой специфики: они основаны на одной общей идее, принадлежащей Карлу Пирсону [см. Pearson (1900)]. Эта идея состоит в использовании в качестве статистики определенной меры расхождения между данными и моделью. Вектор данных (или таблица частот) определяет координаты точки в многомерном пространстве, и расхождение оценивается как обобщенное расстояние [см. раздел 7.2.2] между этой точкой и точкой, определяемой вектором ожидаемых частот, полученных с помощью модели. Основной характерной чертой этого метода является то, что выборочное распределение функции расстояния в большинстве случаев отлично аппроксимируется распределением [см. раздел 2.5.4,а)]. Это верно при любом распределении, лишь число степеней свободы зависит от более детального исследования модели и структуры данных.

Критерий можно пояснить с помощью модели, описывающей одномерное распределение вероятностей, где данные представлены в виде таблицы частот, как в следующих примерах.

Пример 7.2.1. Данные Уэлдона об игральных костях. Это данные о количестве очков, полученных в ставшем теперь уже классическим эксперименте с игральными костями. В повторных бросаниях двенадцати костей количество очков, превышающее 4 на какой-либо одной кости, рассматривалось как «успех», и число успехов 12 костей записывалось для 26306 повторных бросаний. Эти частоты фиксировались в табл. 7.2.1, приведенной из работы [Fisher (1970), табл. 10-С], и сравнивались с ожидаемыми частотами в предположении, что каждая кость идеальна. В последнем случае вероятность успеха для любой

кости была бы равна и вероятность успехов среди 12 костей 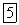вычислялась бы согласно биномиальному распределению [см. II, раздел 5.2.2]:

а ожидаемая частота исхода успехов» была бы равна [см. II, табл. 6.4.2]. Расхождения оказываются весьма значительными. Это может быть следствием того, что кости на самом деле не являются идеальными. Так как количество очков, выпавшее на одной отдельно взятой кости, не идентифицировано, то лучшее, что мы можем сделать, это счесть, что все кости дают одинаковое смещение, и оценить его. Если мы обозначим эту общую вероятность успеха через 0, то по данным найдем оценку максимального правдоподобия для 0:

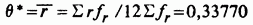
[см. пример 6.3.2]. Если мы пересчитаем ожидаемые частоты в предположении, что параметр один и тот же для всех костей и равен , то получим для ожидаемых частот

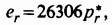
где

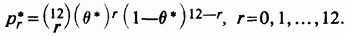
Таблица 7.2.1. (см. скан) Наблюденные и ожидаемые частоты успехов

Численные значения представлены в табл. 7.2.2. Эта модель дает лучшее согласие, большинство расхождений по абсолютной величине меньше соответствующих величин из габл. 7.2.1.

Таблица 7.2.2. (см. скан) Наблюденные и ожидаемые частоты успехов с костями, имеющими одинаковое смещение

(см. скан)

Теперь, очевидно, нужен способ объединения индивидуальных расхождений в единую статистику, которую можно было бы взять как меру расстояния между вектором наблюденных частот и вектором ожидаемых частот. Именно это и дает статистика согласия Карла Пирсона, определяемая как

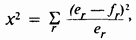
где — наблюдаемая частота в ячейке с номером — соответствующая ожидаемая частота; сумма берется по всем наблюдениям (ячейкам).

В разделе 2.9.4 было показано, что совместное выборочное распределение является мультиномиальным , где k обозначает число ячеек (k = 13 в табл. 7.2.2), с индексом и с вероятностями

где вероятность того, что наблюдение попадет в ячейку с номером . Таким образом,

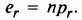
Можно показать, что [см. Cramer (1946), разделы 30.1, 30.3 — С] выборочное распределение приближается распределением суммы квадратов стандартных нормальных случайных величин (где 5 — число оцениваемых параметров). Эта аппроксимация следует из того, что мультиномиальное распределение может быть аппроксимировано многомерным нормальным распределением, точно так же как биномиальное распределение при соответствующих условиях аппроксимируется нормальным распределением. Аппроксимации замечательно устойчивы, но в действительности предполагается, что должна быть не слишком малой (насколько малой — см. раздел 7.3). Когда ожидаемая частота в ячейке опускается ниже критического значения [см. раздел 7.3], эту ячейку приходится объединять с одной или более ее непосредственными соседями так, чтобы новая ожидаемая частота стала выше запрещенного уровня; при этом наблюденные частоты также должны быть соответствующим образом объединены.

Очевидно, что статистика по величине будет малой, когда согласие между наблюденной и ожидаемой частотой хорошее, и большой, когда согласие плохое. Вопрос, является ли данное значение статистики достаточно малым для того, чтобы приписать его случайным флуктуациям, указывая тем самым на приемлемое согласие, должен обсуждаться в терминах выборочного распределения статистики

Выборочное распределение статистики К. Пирсона. Выборочное распределение является (приблизительно) распределением хи-квадрат с числом степеней свободы которое вычисляется по следующему правилу:

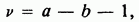
где а — число элементов в столбце «Наблюденные частоты» (считая каждую группу объединенных частот как один элемент) и — число параметров вероятностной модели, которые должны быть оценены по тем же данным. По этой причине критерий назван критерием согласия (или критерием Пирсона). Из определения следует, и это иллюстрируется в последующих примерах, что для смешивает вместе все расхождения между наблюдением и ожиданием, какова бы ни была их природа. Отклонение от проверяемой гипотезы будет всегда приводить к увеличению значения и уровень значимости поэтому всегда вычисляется с помощью односторонней процедуры [см. раздел 5.2.3] следующим образом:

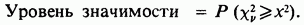
Случай, когда является специальным, к нему неприменимо сказанное выше. Он обсуждается в разделе 7.4.1.

Терминология. Читателей следует предупредить, что статистика Пирсона, которую мы назвали часто называется Пирсона или просто Мы, таким образом, сталкиваемся с запутанной ситуацией, когда статистика, называемая имеет выборочное распределение, лишь приближенно совпадающее с распределением . В этой книге мы пытаемся избежать этой двусмысленности, сохраняя обозначение для случайной величины, имеющей распределение хи-квадрат, или для названия этого распределения.

Пример 7.2.2. Статистика Пирсона для данных об игральных костях из примера 7.2.1. Рассмотрим вычисление для данных о бросании игральных костей из примера 7.2.1 сначала при гипотезе, что кости идеальны, а затем при гипотезе, что игральные кости имеют одинаковое смещение с .

При справедливости первой гипотезы ожидаемые частоты [см. табл. 7.2.2] слишком малы, чтобы использовать распределение как достаточно точное приближение к выборочному распределению Какие ожидаемые частоты считать приемлемо малыми, сказано ниже. Сумма

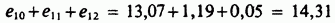
является достаточно большой. Вот почему наблюденные частоты были объединены в табл. 7.2.3. Объединенная частота 18 сравнивалась с соответствующими объединенными ожидаемыми частотами Их общий вклад был равен: Этот вклад в величину представлен последним элементом в предпоследнем столбце табл. 7.2.3. Таким образом, хотя исходная таблица частот содержала 13 элементов в столбце частот (а именно операция объединения сократила их число до 11, а именно Величина равна 35,491.

В случае, когда кости идеальны, величина в определяется этой гипотезой и никакие параметры не следует оценивать по данным. Число степеней свободы равно, таким образом,

Уровень значимости статистики при гипотезе, что кости идеальны, равен приблизительно

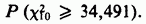
Эта величина меньше, чем что служит сильным аргументом против принятия этой гипотезы.

При гипотезе, что кости имеют одинаковое смещение, обращаясь к табл. 7.2.2, видим, что слишком малы для успешного использования -аппроксимации, и снова рекомендуется объединить последние три частоты. Величина оказывается равной 8,179, и на этот раз число степеней свободы равно:

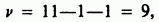
поскольку один параметр должен быть оценен по данным. Уровень значимости статистики при справедливости гипотезы, что кости имеют одинаковое смещение, равен

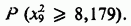
Это число равно примерно 0,5, что представляет собой довольно большую вероятность. Поэтому данные следует рассматривать как не противоречащие этой гипотезе.

Таблица 7.2.3. (см. скан)

Пример 7.2.3. Проверка согласия для пуассоновского распределения. Данные в табл. 3.2.1 являются частотами, с которыми частиц испускались некоторым радиоактивным источником в течение интервалов в 7,5 секунд. Вероятностная модель, диктуемая физикой радиоактивных процессов, предполагает, что величина — число частиц, испускаемых в случайно выбранный 7,5-секундный интервал — имеет пуассоновское распределение вероятностей

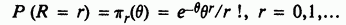
(см. II, раздел 20.1), где в пропорциональна интенсивности радиоактивного излучения образца.

Таблица 7.2.4. (см. скан)

Величина в может быть оценена по данным. Оценка максимального правдоподобия в равна: [см. пример 6.7.1]. Оцененная ожидаемая частота наблюдения будет равна тогда , где — объем выборки. Численные значения представлены в табл. 7.2.4, при записи результатов экспериментов частоты были объединены в

В учебниках часто говорится, что наименьшая ожидаемая частота, при которой можно пользоваться аппроксимацией распределением равна 5; если принять эту рекомендацию, то элементы последних двух строк таблицы должны быть объединены. В результате получим

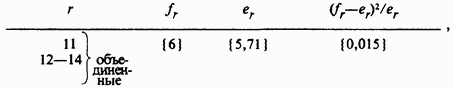
что приводит к

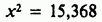
с числом степеней свободы

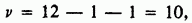
т. е. теперь имеется 12 эффективных частот, а именно

Уровень значимости этого значения при гипотезе, что распределение величины является распределением Пуассона, равен

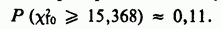
Это большая вероятность, и данные следует рассматривать как вполне согласующиеся с гипотезой о пуассоновском распределении.

Согласно обстоятельным исследованиям У. Кокрена рекомендация использовать ожидаемые частоты не меньше пяти является чрезмерно ограничительной, и для распределений типа тех, с которыми мы имеем дело, достаточно требовать, чтобы частоты были не меньше 1 [см. раздел 7.3]. В нашем примере поэтому никакого объединения производить не следует, кроме того, которое уже было сделано в табл. 7.2.4. Величина тогда равна 15,355 с а так как

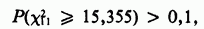
данные совместимы с гипотезой о пуассоновском распределении: результат тот же, что и полученный ранее.