Известная теорема Я. Бернулли, устанавливающая связь между частотой события и его вероятностью, может быть доказана как прямое следствие закона больших чисел.
Пусть производится 
независимых опытов, в каждом из которых может появиться или не появиться некоторое событие 
, вероятность которого в каждом опыте равна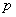 
. Теорема Я. Бернулли утверждает, что при неограниченном увеличении числа опытов частота события сходится по вероятности к его вероятности .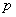
Обозначим частоту события в опытах через 
и запишем теорему Я. Бернулли в виде формулы
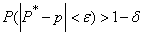, (13.5.1)
где,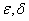 
- сколь угодно малые положительные числа.
Требуется доказать справедливость этой формулы при достаточно большом .
Доказательство. Рассмотрим независимые случайные величины:
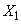- число появлений события в первом опыте;
- число появлений события во втором опыте, и т. д.
Все эти величины прерывны и имеют один и тот же закон распределения, выражаемый рядом вида:
| 
|
|
|
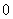
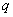
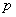
где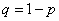 
. Математическое ожидание каждой из величин 
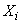равно 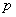, а ее дисперсия 
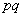(см. 
10.3).
Частота представляет собой не что иное, как среднее арифметическое величин 
:
,
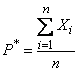и, согласно закону больших чисел, сходится по вероятности к общему математическому ожиданию этих случайных величин. Отсюда и следует справедливость неравенства (13.5.1).
Теорема Я. Бернулли утверждает устойчивость частоты при постоянных условиях опыта. Но при изменяющихся условиях опыта аналогичная устойчивость также существует. Теорема, устанавливающая свойство устойчивости частот при переменных условиях опыта, называется теоремой Пуассона и формулируется следующим образом:
Если производится независимых опытов и вероятность появления события в 
-м опыте равна 
, то при увеличении частота события сходится по вероятности к среднему арифметическому вероятностей .
Теорема Пуассона выводится из обобщенной теоремы Чебышева точно так же, как теорема Бернулли была выведена из закона больших чисел.
Теорема Пуассона имеет большое принципиальное значение для практического применения теории вероятностей. Дело в том, что зачастую вероятностные методы применяются для исследования явлений, которые в одних и тех же условиях не имеют шансов повториться достаточно много раз, но повторяются многократно при весьма разнообразных условиях, причем вероятности интересующих нас событий сильно зависят от этих условий. Например, вероятность поражения цели в воздушном бою существенно зависит от дальности стрельбы, ракурса цели, высоты полета, скорости стреляющего самолета и цели и т. д. Комплекс этих условий слишком многочислен для того, чтобы можно было рассчитывать на многократное осуществление воздушного боя именно в данных фиксированных условиях. И все же, несмотря на это, в данном явлении налицо определенная устойчивость частот, а именно частота поражения цели в реальных воздушных боях, осуществляемых в самых разных условиях, будет приближаться к средней вероятности поражения цели, характерной для данной группы условий. Поэтому те методы организации стрельбы, которые основаны на максимальной вероятности поражения цели, будут оправданы и в данном случае, несмотря на то, что нельзя ожидать подлинной массовости опытов в каждом определенном комплексе условий.
Аналогичным образом обстоит дело в области опытной проверки вероятностных расчетов. На практике очень часто встречается случай, когда требуется проверить на опыте соответствие вычисленной вероятности какого-либо события его фактической частоте. Чаще всего это делается для того, чтобы проверить правильность той или иной теоретической схемы, положенной в основу метода вычисления вероятности события. Зачастую при такой экспериментальной проверке не удается воспроизвести достаточно много раз одни и те же условия опыта. И все же эта проверка может быть осуществлена, если сравнить наблюденную в опыте частоту события не с его вероятностью для фиксированных условий, а со средним арифметическим вероятностей, вычисленных для различных условий.
12. В предыдущем n° мы ввели в рассмотрение ряд распределения как исчерпывающую характеристику (закон распределения) прерывной случайной величины. Однако эта характеристика не является универсальной; она существует только для прерывных случайных величин. Нетрудно убедиться, что для непрерывнойслучайной величины такой характеристики построить нельзя. Действительно, непрерывная случайная величинаимеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток (так называемое «счетное множество»). Составить таблицу, в которой были бы перечислены все возможные значения такой случайной величины, невозможно. Кроме того, как мы увидим в дальнейшем, каждое отдельное значение непрерывной случайной величины обычно не обладает никакой отличной от нуля вероятностью. Следовательно, для непрерывной случайной величины не существует ряда распределения в том смысле, в каком он существует для прерывной величины. Однако различные области возможных значений случайной величины все же не являются одинаково вероятными, и для непрерывной величины существует «распределение вероятностей», хотя и не в том смысле, как для прерывной.
Для количественной характеристики этого распределения вероятностей удобно воспользоваться не вероятностью события 
, а вероятностью события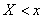 
, где 
– некоторая текущая переменная. Вероятностьэтого события, очевидно, зависит от , есть некоторая функция от . Эта функция называется функцией распределения случайной величины 
и обозначается 
:
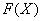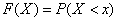. (5.2.1)
Функцию распределения 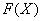иногда называют также интегральной функцией распределения или интегральным законом распределения.
Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как прерывных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.
Сформулируем некоторые общие свойства функции распределения.
1. Функция распределения 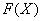есть неубывающая функция своего аргумента, т.е. при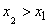 
.
2. На минус бесконечности функция распределения равна нулю: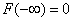 
.
3. На плюс бесконечности функция распределения равна единице: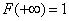 
.
Не давая строгого доказательства этих свойств, проиллюстрируем их с помощью наглядной геометрической интерпретации. Для этого будем рассматривать случайную величину как случайную точку на оси Ох (рис. 5.2.1), которая в результате опыта может занять то или иное положение. Тогда функция распределения 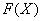естьвероятность того, что случайная точка в результате опыта попадет левее точки .
Рис. 5.2.1.
Будем увеличивать , т. е. перемещать точку вправо по оси абсцисс. Очевидно, при этом вероятность того, что случайная точка попадет левее , не может уменьшиться; следовательно, функция распределения 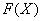с возрастанием убывать не может.
Чтобы убедиться в том, что 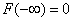, будем неограниченно перемещать точку влево по оси абсцисс. При этом попадание случайной точки левее в пределе становится невозможным событием; естественно полагать, что вероятность этого события стремится к нулю, т.е. .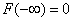
Аналогичным образом, неограниченно перемещая точку вправо, убеждаемся, что 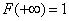, так как событие 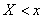становится в пределе достоверным.
График функции распределения в общем случае представляет собой график неубывающей функции (рис. 5.2.2), значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь скачки (разрывы).
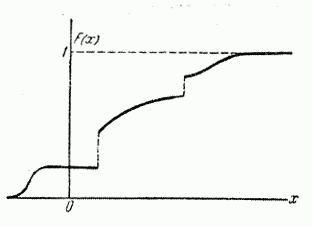
Рис. 5.2.2.
Зная ряд распределения прерывной случайной величины, можно легко построить функцию распределения этой величины. Действительно,
,
где неравенство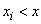 
под знаком суммы указывает, что суммирование распространяется на все те значения 
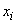, которые меньше .
Когда текущая переменная проходит через какое-нибудь из возможных значений прерывной величины , функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.
Пример 1. Производится один опыт, в котором может появиться или не появиться событие . Вероятность события равна 0,3. Случайная величина – число появлений события в опыте (характеристическая случайная величина события ). Построить её функцию распределения.
Решение. Ряд распределения величины имеет вид:
Построим функцию распределения величины :
1) при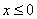 
;
2) при 
;
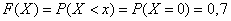3) при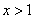 
.
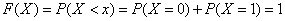График функции распределения представлен на рис. 5.2.3. В точках разрыва функция 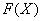принимает значения, отмеченные на чертеже точками (функция непрерывна слева).
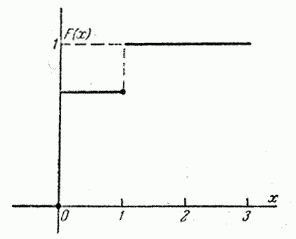
Рис. 5.2.3.
Пример 2. В условиях предыдущего примера производится 4 независимых опыта. Построить функцию распределения числа появлений события .
Решение. Обозначим – число появлений события в четырех опытах. Эта величина имеет ряд распределения
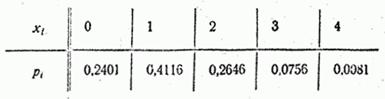
Построим функцию распределения случайной величины :
1) при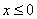 
;
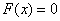2) при 
;
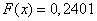3) при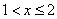 
;
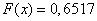4) при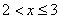 
;
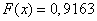5) при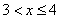 
;
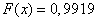6) при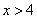 
.
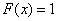График функции распределения представлен на рис. 5.2.4.
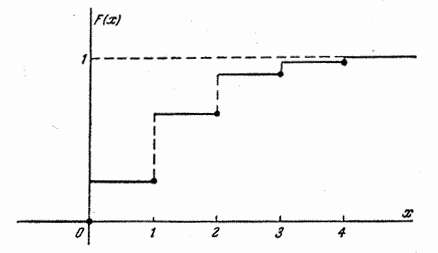
Рис. 5.2.4.
Функция распределения любой прерывной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным случайным значениям величины, и равны вероятностямэтих значений. Сумма всех скачков функции 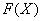равна единице.
По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними скачков становится больше, а сами скачки – меньше; ступенчатая кривая становится более плавной (рис. 5.2.5); случайна величина постепенно приближается к непрерывной величине, а её функция распределения – к непрерывной функции (рис. 5.2.6).
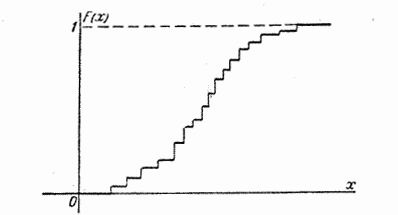
Рис. 5.2.5.
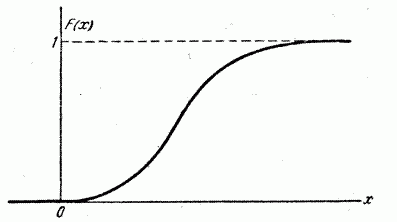
Рис. 5.2.6.
На практике обычно функция распределения непрерывной случайной величины представляет собой функцию, непрерывную во всех точках, как это показано на рис. 5.2.6. Однако можно построить примеры случайных величин, возможные значения которых непрерывно заполняют некоторый промежуток, но для которых функция распределения не везде является непрерывной, а в отдельных точках терпит разрыв (рис. 5.2.7).
Рис. 5.2.7.
Такие случайные величины называются смешанными. В качестве примера смешанной величины можно привести площадь разрушений, наносимых цели бомбой, радиус разрушительного действия которой равен R (рис. 5.2.8).
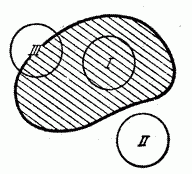
Рис. 5.2.8.
Значения этой случайной величины непрерывно заполняют промежуток от 0 до 
, осуществляющиеся при положениях бомбы типа I и II, обладают определенной конечной вероятностью, и этим значениям соответствуют скачки функции распределения, тогда как в промежуточных значениях (положение типа III) функция распределения непрерывна. Другой пример смешанной случайной величины – время T безотказной работы прибора, испытываемого в течение времени t. Функция распределения этой случайной величины непрерывна всюду, кроме точки t.
Плотность распределения
Пусть имеется непрерывная случайная величина с функцией распределения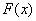 
, которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от до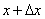 
:
,
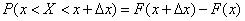т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать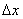 
к нулю. В пределе получим производную от функции распределения:
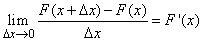. (5.4.1)
Введем обозначение:
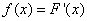. (5.4.2)
Функция 
- производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины .
Термины «плотность распределения», «плотность вероятности» становятся особенно наглядными при пользовании механической интерпретацией распределения; в этой интерпретации функция буквально характеризует плотность распределения масс по оси абсцисс (так называемую «линейную плотность»). Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 5.4.1).
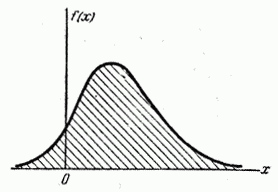
Рис. 5.4.1.
Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.
Рассмотрим непрерывную случайную величину с плотностью распределения и элементарный участок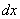 
, примыкающий к точке (рис. 5.4.2). Вероятность попадания случайной величины на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна 
. Величина называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок 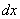(рис. 5.4.2).
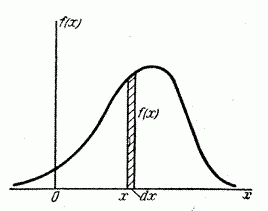
Рис. 5.4.2.
Выразим вероятность попадания величины на отрезок от 
до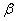 
(рис 5.4.3) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т.е. интегралу:
(5.4.3)
*) Так как вероятность любого отдельного значения непрерывной случайной величины равна нулю, то можно рассматривать здесь отрезок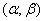 
, не включая в него левый конец, т.е. отбрасывая знак равенства в 
.
Геометрически вероятность попадания величины на участок 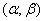равна площади кривой распределения, опирающейся на этот участок (рис. 5.4.3.).
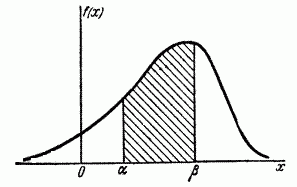
Рис. 5.4.3.
Формула (5.4.2.) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению
,
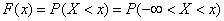откуда по формуле (5.4.3) имеем:
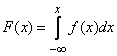. (5.4.4)
Геометрически 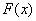есть не что иное, как площадь кривой распределения, лежащая левее точки (рис. 5.4.4).
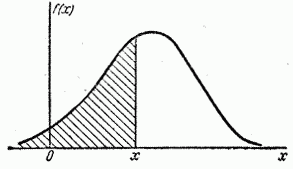
Рис. 5.4.4.
Укажем основные свойства плотности распределения.
1. Плотность распределения есть неотрицательная функция:
.
Это свойство непосредственно вытекает из того, что функция распределения 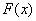есть неубывающая функция.
2. Интеграл в бесконечных пределах от плотности распределения равен единице:
.
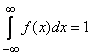Это следует из формулы (5.4.4) и из того, что .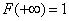
Геометрически основные свойства плотности распределения означают, что:
1) вся кривая распределения лежит не ниже оси абсцисс;
2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Выясним размерность основных характеристик случайной величины – функции распределения и плотности распределения. Функция распределения 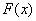, как всякая вероятность, есть величина безразмерная. Размерность плотности распределения , как видно из формулы (5.4.1), обратна размерности случайной величины.
Пример 1. Функция распределения непрерывной случайной величины Х задана выражением
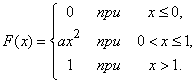
а) Найти коэффициент а.
б) Найти плотность распределения .
в) Найти вероятность попадания величины на участок от 0,25 до 0,5.
Решение. а) Так как функция распределения величины непрерывна, то при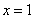 
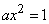, откуда 
.
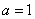б) Плотность распределения величины выражается формулой
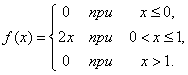
в) По формуле (5.3.1) имеем:
.
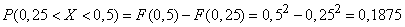Пример 2. Случайная величина подчинена закону распределения с плотностью:
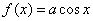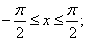
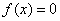при 
при 
или 
.
а) Найти коэффициент а.
б) Построить график плотности распределения .
в) Найти функцию распределения 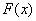и построить её график.
г) Найти вероятность попадания величины на участок от 0 до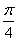 
.
Решение. а) Для определения коэффициента а воспользуемся свойством плотности распределения:
,
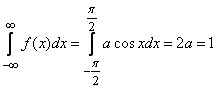откуда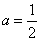 
.
б) График плотности представлен на рис. 5.4.5.
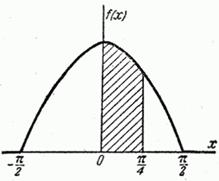
Рис. 5.4.5.
в) По формуле (5.4.4) получаем выражение функции распределения:
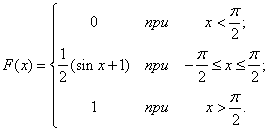
График функции 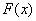изображен на рис. 5.4.6.
Рис. 5.4.6.
г) По формуле (5.3.1) имеем:
.
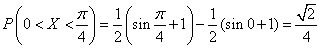Тот же результат, но несколько более сложным путем, можно получить по формуле (5.4.3).
Пример 3. Плотность распределения случайной величины задана формулой:
.
а) Построить график плотности .
б) Найти вероятность того, что величина попадет на участок (-1, +1).
Решение. а) График плотности дан на рис. 5.4.7.
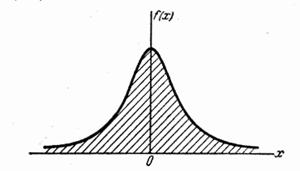
Рис. 5.4.7.
б) По формуле (5.4.3) имеем:
.
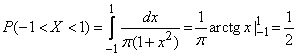14. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ (гауссово) (или распределение нормальной случайной величины ) — распределение вероятностей, задаваемое дифференциальным законом (функцией):
,
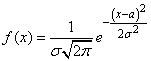здесь 
— математическое ожидание случайной величины , 
— среднеквадратическое отклонение , — плотность вероятности случайной величины в точке . Графики функций при различных , приведены на рисунке 21. Рисунок иллюстрирует зависимость кривых от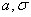 
: вершина кривой имеет абсциссу 
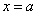, кривая симметрична относительно прямой 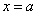, большему соответствует пологая кривая, малому — островершинная, крутая кривая; точки перегиба кривой имеют абсциссы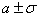 
. Площадь под каждой из кривых равна 1.
Рис. 21
Дифференциальная функция , задающая, нормальную случайную величину , позволяет вычислить вероятности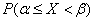 
того, что случайная величина примет свое значение в интервале 
:
. (*)
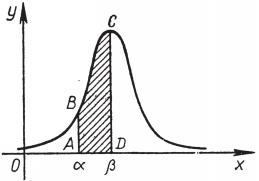
Рис. 22
Формула (*) может быть истолкована в геометрических терминах: вероятность 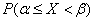численно равна площади криволинейной трапеции 
(рис. 22). Поскольку первообразная функции не является элементарной функцией, вычисление интегралов (*) производят с помощью таблиц функции
,
называемой Лапласа функцией. Именно:
, 
, 
.
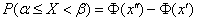Легко вычислить, что
,
,
.
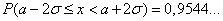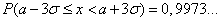Эти соотношения называют правилами одной, двух и трех сигм соответственно. Последняя формула означает, что событие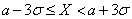 
почти всегда наступает ( 
). Такое событие называют практически достоверным событием.
Н. р., а также нормальная случайная величина называются также распределением Гаусса и гауссовой случайной величиной.
Н. р. играет исключительно важную роль в теории вероятности и математической статистике. Причиной этому являются те общие свойства случайных величин, которые формируются в предельных теоремах теории вероятностей и, в особенности, в центральной предельной теореме А. М. Ляпунова. Согласно этой теореме всякая случайная величина , равная сумме большого количества «мелких» независимых случайных величин, имеет распределение, близкое к Н. р. При этом на практике часто встречаются случайные величины с указанным выше свойством, что позволяет считать распределение случайной величины близким к Н. р.
Совместное распределение нескольких случайных величин называется многомерным Н. р., если дифференциальный закон этого распределения имеет вид:
,
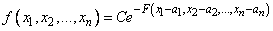где 
, 
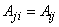— положительно определенная квадратическая форма.
Постоянная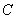 
такова, что интеграл 
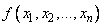по всему пространству равняется единице. Числа 
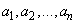являются математическими ожиданиями случайных величин 
соответственно, а коэффициент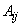 
выражается через дисперсии 
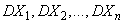этих величин и через коэффициенты корреляции 
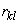величин 
; 
.
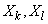Равномерное распределение.
Наиболее простым является равномерное распределение (рис. 2.17), для которого плотность вероятност и постоянна для данного интервала 
и равна нулю за его пределами, т.е.
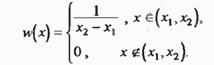
Если, например, измерение какой-либо величины производится с точностью до целого числа делений шкалы измерительного прибора, так что ошибки, превосходящие по абсолютному значению половину деления (или половину тага квантования в приборах с цифровым
Рис. 2.17. Плотность вероятности при равномерном распределении
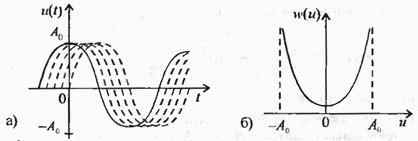
Рис. 2.18 Гармонический сигнал со случайной фазой, его (а) реализация и (б) плотность вероятности
отсчётом), практически невозможны, то ошибка измерений 8 представляет собой равномерно распределённую 
Возможными значениями 
являются в этом смысле действительные числа, не превосходящие по абсолютной величине половину деления шкалы.
Классическими примерами, связанными с Н. р., являются задача о броуновском движении, задача о распределении ошибок наблюдения (К. Ф. Гаусс), задача о распределении скоростей молекул (Дж. К. Максвелл).
Закон Пуассона
Во многих задачах практики приходится иметь дело со случайными величинами, распределенными по своеобразному закону, который называется законом Пуассона.
Рассмотрим прерывную случайную величину , которая может принимать только целые, неотрицательные значения:
,
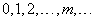причем последовательность этих значений теоретически не ограничена.
Говорят, что случайная величина распределена по закону Пуассона, если вероятность того, что она примет определенное значение 
, выражается формулой
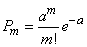
, (5.9.1)
где а – некоторая положительная величина, называемая параметром закона Пуассона.
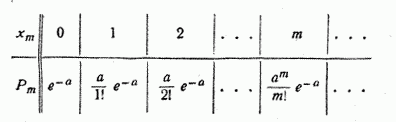
Ряд распределения случайной величины , распределенной по закону Пуассона, имеет вид:
Убедимся, прежде всего, что последовательность вероятностей, задаваемая формулой (5.9.1), может представлять собой ряд распределения, т.е. что сумма всех вероятностей 
равна единице. Имеем:
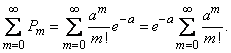
Но
,
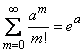откуда
.
На рис. 5.9.1 показаны многоугольники распределения случайной величины , распределенной по закону Пуассона, соответствующие различным значениям параметра . В таблице 8 приложения приведены значения для различных .
Рис. 5.9.1.
Определим основные характеристики – математическое ожидание и дисперсию – случайной величины , распределенной по закону Пуассона. По определению математического ожидания
.
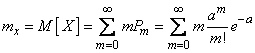Первый член суммы (соответствующий 
) равен нулю, следовательно, суммирование можно начать с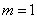 
:
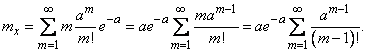
Обозначим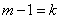 
; тогда
. (5.9.2)
Таким образом, параметр представляет собой не что иное, как математическое ожидание случайной величины .
Для определения дисперсии найдем сначала второй начальный момент величины :
По ранее доказанному
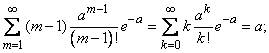
кроме того,
следовательно,
Далее находим дисперсию величины :
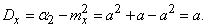(5.9.3)
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна её математическому ожиданию .
Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
Определим для случайной величины , распределенной по закону Пуассона, вероятность того, что она примет значение не меньше заданного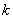 
. Обозначим эту вероятность 
:
.
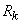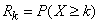Очевидно, вероятность 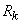может быть вычислена как сумма
Однако значительно проще определить её из вероятности противоположного события:
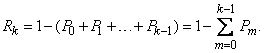(5.9.4)
В частности, вероятность того, что величина примет положительное значение, выражается формулой
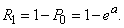(5.9.5)
Мы уже упоминали о том, что многие задачи практики приводят к распределению Пуассона. Рассмотрим одну из типичных задач такого рода.
Рис. 5.9.2.
Пусть на оси абсцисс Ох случайным образом распределяются точки (рис. 5.9.2). Допустим, что случайное распределение точек удовлетворяет следующим условиям:
1. Вероятность попадания того или иного числа точек на отрезок 
зависит только от длины этого отрезка, но не зависит от его положения на оси абсцисс. Иными словами, точки распределяются на оси абсцисс с одинаковой средней плотностью. Обозначим эту плотность (т.е. математическое ожидание числа точек, приходящихся на единицу длины) через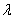 
.
2. Точки распределяются на оси абсцисс независимо друг от друга, т.е. вероятность попадания того или другого числа точек на заданный отрезок не зависит от того, сколько их попало на любой другой отрезок, не перекрывающийся с ним.
3. Вероятность попадания на малый участок 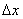двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек).
Выделим на оси абсцисс определенный отрезок длины и рассмотрим дискретную случайную величину – число точек, попадающих на этот отрезок. Возможные значения величины будут
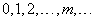(5.9.6)
Так как точки попадают на отрезок независимо друг от друга, то теоретически не исключено, что их там окажется сколь угодно много, т.е. ряд (5.9.6) продолжается неограниченно.
Докажем, что случайная величина имеет закон распределения Пуассона. Для этого вычислим вероятность того, что на отрезок попадет ровно 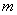точек.
Сначала решим более простую задачу. Рассмотрим на оси Ох малый участок 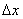и вычислим вероятность того, что на этот участок попадет хотя бы одна точка. Будем рассуждать следующим образом. Математическое ожиданиечисла точек, попадающих на этот участок, очевидно, равно 
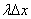(т.к. на единицу длины попадает в среднем 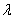точек). Согласно условию 3 для малого отрезка 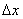можно пренебречь возможностью попадания на него двух или больше точек. Поэтому математическое ожидание 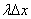числа точек, попадающих на участок 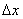, будет приближенно равно вероятности попадания на него одной точки (или, что в наших условиях равнозначно, хотя бы одной).
Таким образом, с точностью до бесконечно малых высшего порядка, при 
можно считать вероятность того, что на участок 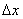попадет одна (хотя бы одна) точка, равной 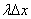, а вероятность того, что не попадет ни одной, равной 
.
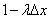Воспользуемся этим для вычисления вероятности попадания на отрезок ровно 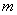точек. Разделим отрезок на равных частей длиной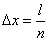 
. Условимся называть элементарный отрезок 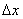«пустым», если в него не попало ни одной точки, и «занятым», если в него попала хотя бы одна. Согласно выше доказанному вероятность того, что отрезок 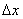окажется «занятым», приближенно равна 
; вероятность того, что он окажется «пустым», равна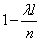 
. Так как, согласно условию 2, попадания точек в неперекрывающиеся отрезки независимы, то наши n отрезков можно рассмотреть как независимых «опытов», в каждом из которых отрезок может быть «занят» с вероятностью 
. Найдем вероятность того, что среди отрезков будет ровно 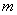«занятых». По теореме о повторении опытов эта вероятность равна
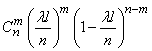
или, обозначая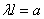 
,
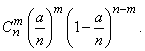(5.9.7)
При достаточно большом эта вероятность приближенно равна вероятности попадания на отрезок ровно 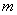точек, так как попадание двух или больше точек на отрезок 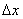имеет пренебрежимо малую вероятность. Для того чтобы найти точное значение , нужно в выражении (5.9.7) перейти к пределу при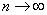 
:
(5.9.8)
Преобразуем выражение, стоящее под знаком предела:
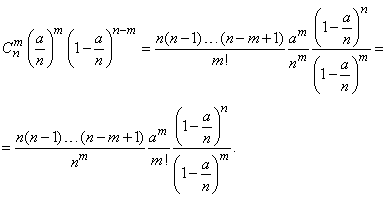(5.9.9)
Первая дробь и знаменатель последней дроби в выражении (5.9.9) при 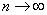, очевидно, стремятся к единице. Выражение 
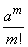от не зависит. Числитель последней дроби можно преобразовать так:
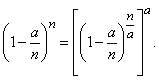(5.9.10)
При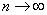 
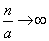и выражение (5.9.10) стремится к 
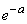. Таким образом, доказано, что вероятность попадания ровно 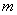точек в отрезок выражается формулой
,
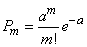где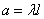 
, т.е. величина Х распределена по закону Пуассона с параметром .
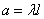Отметим, что величина по смыслу представляет собой среднее число точек, приходящееся на отрезок .
Величина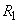 
(вероятность того, что величина Х примет положительное значение) в данном случае выражает вероятность того, что на отрезок попадет хотя бы одна точка:
. (5.9.11)
Таким образом, мы убедились, что распределение Пуассона возникает там, где какие-то точки (или другие элементы) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек, попавших в какую-то область. В нашем случае такой «областью» был отрезок на оси абсцисс. Однако наш вывод легко распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
1) точки распределены в поле статистически равномерно со средней плотностью ;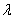
2) точки попадают в неперекрывающиеся области независимым образом;
3) точки появляются поодиночке, а не парами, тройками и т.д., то число точек , попадающих в любую область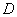 
(плоскую или пространственную), распределяются по закону Пуассона:
,
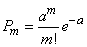
где – среднее число точек, попадающих в область .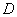
Для плоского случая
,
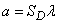где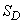 
– площадь области 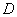; для пространственного
,
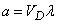где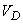 
- объем области .
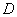Заметим, что для пуассоновского распределения числа точек, попадающих в отрезок или область, условие постоянной плотности (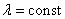 
) несущественно. Если выполнены два других условия, то закон Пуассона все равно имеет место, только параметр а в нем приобретает другое выражение: он получается не простым умножение плотности 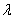на длину, площадь или объем области, а интегрированием переменной плотности по отрезку, площади или объему. (Подробнее об этом см. n° 19.4)
Наличие случайных точек, разбросанных на линии, на плоскости или объеме – неединственное условие, при котором возникает распределение Пуассона. Можно, например, доказать, что закон Пуассона является предельным для биномиального распределения:
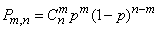, (5.9.12)
если одновременно устремлять число опытов к бесконечности, а вероятность 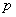– к нулю, причем их произведение 
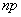сохраняет постоянное значение:
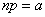. (5.9.13)
Действительно, это предельное свойство биномиального распределения можно записать в виде:
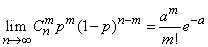. (5.9.14)
Но из условия (5.9.13) следует, что
. (5.9.15)
Подставляя (5.9.15) в (5.9.14), получим равенство
, (5.9.16)
которое только что было доказано нами по другому поводу.
Это предельное свойство биномиального закона часто находит применение на практике. Допустим, что производится большое количество независимых опытов , в каждом из которых событие имеет очень малуювероятность 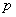. Тогда для вычисления вероятности 
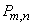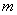того, что событие появится ровно раз, можно воспользоваться приближенной формулой:
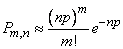, (5.9.17)
где 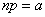- параметр того закона Пуассона, которым приближенно заменяется биномиальное распределение.
От этого свойства закона Пуассона – выражать биномиальное распределение при большом числе опытов и малой вероятности события – происходит его название, часто применяемое в учебниках статистики: закон редких явлений.
Рассмотрим несколько примеров, связанных с пуассоновским распределением, из различных областей практики.
Распределение статистики
Теперь вернемся к тому, что, вероятно, представляет наиболее трудную проблему для начинающего изучать математическую статистику: к понятию распределения статистики (или статистических параметров, таких как среднее значение или дисперсия выборки).
Предположим, что мы сделали ряд измерений и что по этой выборке вычислили одну или несколько статистик. Например, мы можем случайным образом выбрать 1000 американцев из общего населения около 200 миллионов и измерить рост каждого. Исходя из полученных данных, можно вычислить среднее значение выборки х. Дисперсия выборки определяется следующим образом:
Для ясности, обычно используют греческие буквы для обозначения статистик модели и латинские буквы для соответствующей статистики выборки.
Хорошо бы знать указанные два числа для выборки, которую мы взяли. Однако, если от этих чиеел ждут большой пользы, то сразу же возникает вопрос: что разумного можно получить для уточнения среднего значения, если весь процесс повторить снова, используя
Таблица 1.6.1. (см. скан)
Связь статистик выборки и множества
разную случайную выборку 1000 американцев? Короче говоря, что такое «среднее» распределения статистики? Очевидно, повторение всего процесса выбора людей, проведение измерений и вычисление среднего даст нам распределение величин среднего значения х (и распределение дисперсии
В примере с округлением имелась уникальная модель для исходного множества чисел, из которого извлекались округленные значения, а в примере с гауссовым распределением достаточно оценить два неизвестных параметра множества: распределение по статистикам выборки 
Можно поинтересоваться, какая существует связь между этими парами чисел (табл. 1.6.1). В руководствах по статистике доказывается, что для любого распределения среднее выборки есть несмещенная оценка среднего значения исходной совокупности. Аналогично дисперсия выборки 
определяется несмещенной оценкой 
Несмещенная оценка означает, что в среднем оценки не слишком велики и не слишком малы, т. е. среднее значение статистики равно той величине, которая оценивается.
Если выборка достаточно велика 
тогда центральная предельная теорема утверждает, что статистика, называемая средним значением, имеет распределение, очень близкое к гауссовому (нормальному) распределению
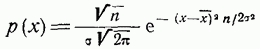
с параметрами 
Дата: 2019-02-19, просмотров: 313.
