Определение 1. Переменная величина принимающая в результате испытания одно из конечной или бесконечной последовательности значений называется дискретной случайной величиной, если каждому Значению соответствует определенная вероятность того, что переменная величина 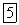примет значение

Из определения следует, что каждому значению соответствует вероятность .

Функциональная зависимость вероятности от называется законом распределения вероятностейдискретной случайной величины х.

Так же закон распределения может быть задан графически в виде многоугольника распределения вероятностей, когда в прямоугольной системе координат строятся точки, с координатами и соединяются ломаной (рис. 409).

Закон распределения может быть задан и аналитически:

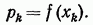
Рис. 409,

То, что случайная величина примет одно из значений последовательности есть событие достоверное, и потому должно выполняться условие

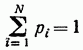
в случае конечной последовательности N значений, или

в случае бесконечной последовательности. Заметим, что значение случайной величины имеющее наибольшую вероятность,

называется модой. Случайная величина изображенная на рис. 409, имеет моду

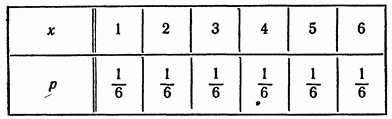
Пример 1. Переменная величина х есть число очков, выпадающее на верхней грани игральной кости при ее однократном бросании. Переменная может принять одно из следующих значений: 1, 2, 3, 4, 5, 6. Вероятность выпадения каждого значения есть, 1/6. Следовательно, таблица распределения этой случайной величины будет иметь вид

Пример 2. Вероятность появления события А при каждом из бесконечной последовательности испытаний равна р. Случайная величина номер испытания, при котором произошло первый раз событие А. Найти закон распределения случайной величины

Решение. Случайная величина может принимать любое целое положительное значение Вероятность того, что событие А произойдет при первом испытании, будет

Вероятность того, что событие не произойдет при первом испытании, а произойдет при втором, будет

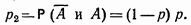
Вероятность того, что событие А не произойдет ни при первом, ни при втором испытании, а произойдет при третьем, будет

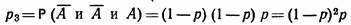
и т. д.

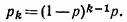
Таблица распределения вероятностей будет

Здесь также имеем:

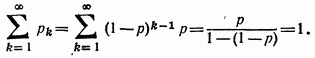
Задача о стрельбе до первого попадания. Рассмотренная задача имеет приложение, в частности, к вопросам стрельбы. Пусть производится стрельба до первого попадания. Вероятность попадания при каждом выстреле есть .

Случайная величина номер выстрела, при котором произошло первое попадание. Таблица распределения вероятностей этой случайной величины будет та же, что и в примере 2.

Пример 3. Вероятность попадания при каждом выстреле Имеется три снаряда. Определить вероятность того, что будет израсходован один снаряд, два снаряда, три снаряда, если стрельба ведется до первого попадания или промаха всеми тремя снарядами: составить таблицу распределения случайной величины х — числа израсходованных снарядов.

Решение. Пусть х — случайная величина: число израсходованных снарядов; - вероятность того, что будет израсходовано снарядов. Тогда равна вероятности попадания при одном (первом) выстреле.

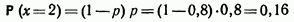
- вероятность того, что при первом выстреле был промах, при втором выстреле — попадание.

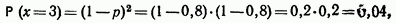
так как всего три снаряда и стрельбу прекращают независимо от того, будет ли при третьем выстреле попадание или промах. Последнюю вероятность можно было вычислить и как разность

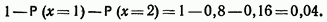
Таблица распределения будет иметь вид

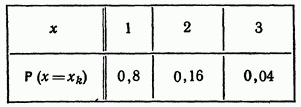
Замечание. Данную задачу можно сформулировать в терминах «схемы урч», следовательно, она может иметь значение и при рассмотрении других вопросов. Это замечание относится и к некоторым другим задачам

Числовые характеристики.

На практике часто ограничиваются рассмотрением хотя и менее полных, но зато более простых характеристик случайных величин (процессов), называемых числовыми характеристиками или моментами. Числовой характеристикой случайной величины может служить момент порядка, определяемый как

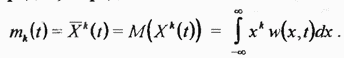
В частности, момент первого порядка, называемый математическим ожиданием определяет среднее значение случайной величины

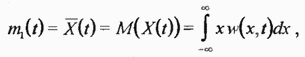
где черта сверху означает усреднение по множеству реализаций. Аналогично вводится момент второго порядка

Разность между случайной величиной X и её представляет собой отклонение от среднего значения. Она называется центрированным значением 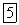квадрата этого отклонения называется дисперсией или центральным моментом второго порядка

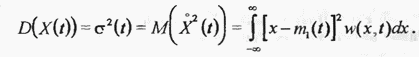
Величину называют стандартным или среднеквадратическим отклонением. С учётом (2.65) и (2.66) выражение (2.67) приводится к результату

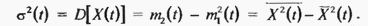
Дисперсия характеризует разброс случайной величины относительно её среднего значения. и дисперсия являются важными характеристиками случайной величины, однако они не дают достаточного представления о изменчивости случайного процесса во времени. При совместном изучении центрированных случайных величин сечений центрированного случайного процесса вводится понятие смешанного момента второго порядка, называемого функцией корреляции

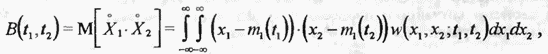
где двумерная плотность вероятности. Функция корреляции характеризует степень статистической взаимосвязи значений случайного процесса в моменты разделённые интервалом (см. рис. 2.15). Убывание ФК с увеличением свидетельствует об ослаблении связи между мгновенными значениями процесса. Если ФК при каких-либо значениях имеет отрицательное значение, это свидетельствует о том, что положительным отклонениям процесса в одном сечении соответствуют преимущественно отрицательные отклонения в другом сечении и наоборот. Если случайные величины и статистически независимы, то их двумерные ПВ определяется произведением одномерных между двумя такими сечениями, как следует из (2.68), равна нулю.