Для облегчения и ускорения подсчетов изучаемых признаков, их средних величин распределения, разнообразия, достоверности, результатов, а также достоверности их различия в сравниваемых группах используют методику вариационных рядов.
Даже получая данные машинной обработки результатов, исследователь должен понимать, что они собой представляют.
Вариационный ряд - ряд чисел, расположенных в ранговом порядке, - обычно от меньшего к большему, реже наоборот, от боль- шего к меньшему.
В медицинской статистике приняты следующие условные обозначения для вариационного ряда:
V - варианты, числовые значения признака;
Р - частота признака, т.е. сумма вариант с данным значением признака;
n - сумма всех частот (общее число всех вариант).
Вариационные ряды бывают простыми - не сгруппированными, которые составляются, как правило, при малом (до 30) числе наблюдений, и сгруппированными, которые составляются при большом (более 30) числе наблюдений.
Основные требования к составлению вариационных рядов:
1. Расположить все варианты по порядку.
2. Суммировать единицы, имеющие одинаковый признак, т.е. найти частоту каждой варианты.
3. Определить число групп и размер интервала.
4. Разбить весь ряд на группы, используя выбранный интервал и строго соблюдая непрерывность сгруппированного ряда.
5. Дать графическое изображение.
Все 5 требований выполняют при составлении сгруппированных вариационных рядов; требования 1, 2 и 5 - при составлении не сгруппированных вариационных рядов.
Число групп в сгруппированном вариационном ряду определяется по табл. 37 в зависимости от числа наблюдений.
Таблица 37. Сгруппированный вариационный ряд
| Число наблюдений | 31-45 | 46-100 | 101-200 | 201-500 |
| Число групп | 6-7 | 8-10 | 11-12 | 13-17 |
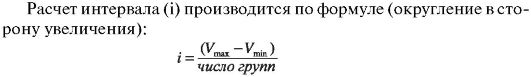
Составление простого вариационного ряда при малом и большом числе наблюдений, составление сгруппированного вариаци- онного ряда и особенности их обработки приводятся ниже.
Графическое изображение вариационного ряда помогает выявить характер распределения признака, т.е. первое свойство статистической совокупности (рис. 9).
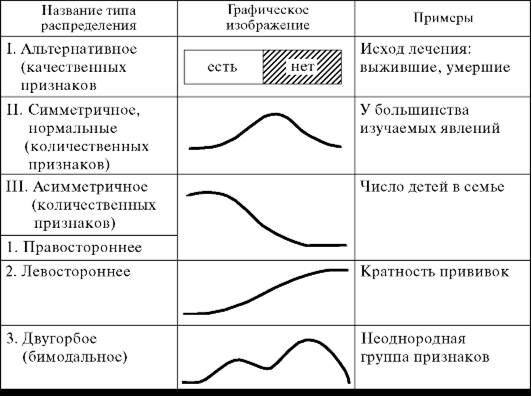
Рис. 9. Основные типы распределения признаков статистической совокупности.
Второе свойство статистической совокупности - средний уровень признака - число, являющееся обобщенной характеристикой того или другого количественного признака статистической совокупности.
Средний уровень признака определяется средними величинами:
1. Мода (Мо) - самая частая варианта.
2. Медиана (Ме) - варианта, расположенная посередине ряда.
3. Средняя арифметическая (М).


где А - условная средняя арифметическая, а = (V-A)/i - отклонение (отличие) каждой варианты от условной средней в интервалах,
i ZaP/n - первый момент средней арифметической (среднее отклонение всех вариант ряда от условной средней).
М по способу моментов вычисляется при большом числе наблюдений. Составление простого вариационного ряда и вычисление средней арифметической как средневзвешенной при большом числе наблюдений показано на примере:
| Рост студентов в см V | Число студентов Ρ | VxP |
| 158 | 1 | 158 |
| 160 | 3 | 480 |
| 162 | 2 | 324 |
| 163 | 4 | 652 |
| 164 | 6 | 984 |
| 165 | 8 | 1320 |
| 166 | 7 | 1162 |
| 168 | 5 | 840 |
| 169 | 6 | 1014 |
| 170 | 5 | 850 |
| 172 | 4 | 688 |
| 174 | 2 | 348 |
| 175 | 2 | 350 |
| 176 | 1 | 176 |
| ΣΡ=η=56 | ΣVΡ=9346 |

Составление группированного вариационного ряда и вычисление средней арифметической по способу моментов при большом числе наблюдений показано в табл. 38
Таблица 38.
| Рост в см | V средняя | Ρ | a=(V-A)/i | АР | a2P |
| Vi=3 | |||||
| 158-160 | 159 | 4 | -1 | -8 | 16 |
| 161-163 | 162 | 6 | -1 | -6 | 6 |
| 164-166 | 165 | 21 | 0 | 0 | 0 |
| 167-169 | 168 | 11 | + 1 | + 11 | 11 |
| 170-172 | 171 | 9 | +2 | + 18 | 36 |
| 173-175 | 174 | 4 | +3 | + 12 | 36 |
| 176-178 | 177 | 1 | +4 | +4 | 16 |
| Σρ=η=56 | Σap=+31 | Σa2P=121 | |||
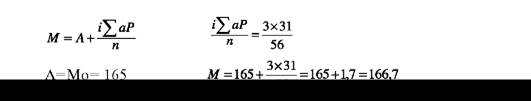
Средние величины должны характеризовать однородную статистическую совокупность.
Третье свойство статистической совокупности - разнообразие признаков: величина того или другого количественного признака неодинакова у всех единиц однородной статистической совокупности.
Это свойство иллюстрируют 3 группы мальчиков, одинаковые по численности и имеющие одинаковую среднюю арифметическую роста (табл. 39).
Среднее квадратичное отклонение (G) - учитывает разнообразие всех вариант со знаком «+» или «-» при числе признаков (n) меньше 30 (n<30):
Таблица 39.

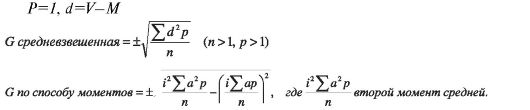
Вычисление среднеквадратичного отклонения (G) при малом числе наблюдений (n<30), например (табл. 40):
Таблица 40.
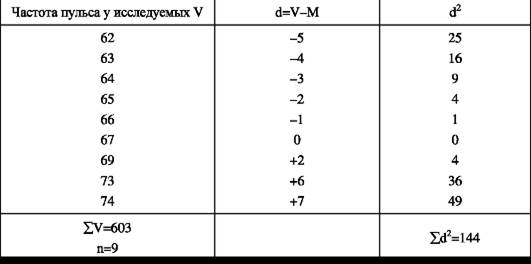
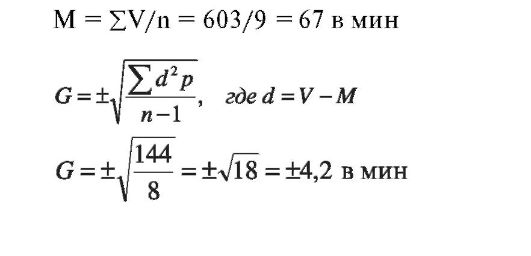
Особенности статистической обработки данных при малом числе наблюдений (n<30):
1. Средняя арифметическая находится как простая.
2. Среднее квадратичное находится как простое, n - 1.
3. Значение t находят по таблице Стьюдента.
Основной смысл названных особенностей - повышение требований к вычислениям.
Вычисление среднего квадратичного отклонения (G) при большом числе наблюдений как средневзвешенного показано на примере (табл. 41).
Таблица 41.
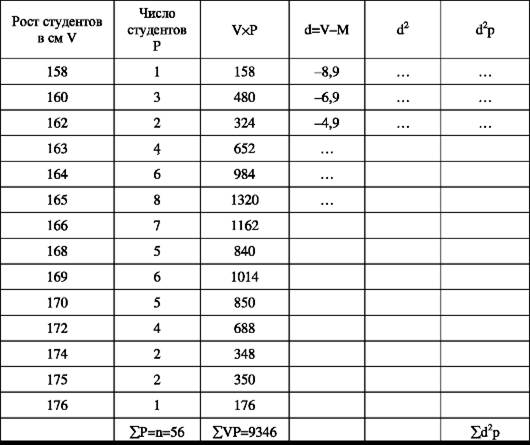

Получаются очень громоздкие вычисления, их упрощают - рассчитывают среднеквадратичное отклонение по способу моментов в сгруппированном вариационном ряду.
Вычисление среднего квадратичного отклонения по способу моментов (второй момент) показано на примере (табл. 42).
Таблица 42.
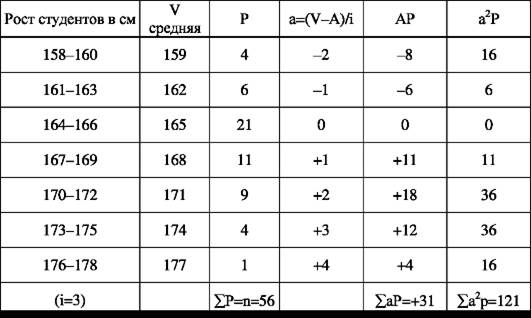
Теорией статистики установлено, что при нормальном распределении М ? σ находится 68% всех вариант, М ? 2σ находится 95,5% всех вариант, М ? 3σ находится 99,7% всех вариант (рис. 10).
По G (среднему квадратичному отклонению) можно определить структуру вариационного ряда; судить о точности (типичности) средней арифметической: если 95% всех вариант находится в пределах Μ?2σ, то средняя арифметическая является типичной (увеличивать число наблюдений не следует); судить о показателях, оценивать отдельные признаки у каждого индивидуума по стандартному отклонению t: сколько сигм составляет отклонение индивидуального признака от средней арифметической:
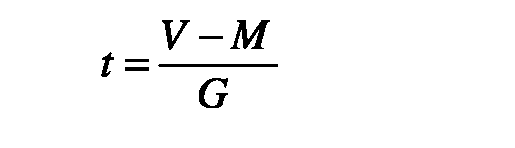
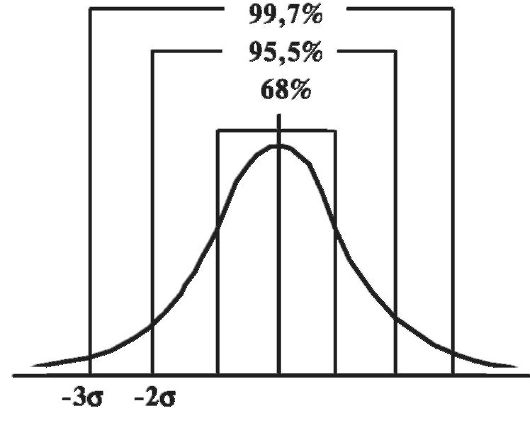
Рис. 10. Связь среднего квадратичного отклонения со структурой вариационного ряда.
Если t<2σ, то отличие индивидуального признака от стандарта незначительно; если t>=2σ, то отличие индивидуального признака от стандартного значительно.
Дата: 2019-02-19, просмотров: 718.