Вся мудрость статистики состоит в том, что по части можно судить о целом. Эта часть - выборочная совокупность должна быть репрезентативна, т.е. представительна по отношению к генеральной совокупности по количеству и качеству (см. ниже).

Формула определения необходимого числа наблюдений (репрезентативной выборки) выводится из формулы «ошибки» путем ал- гебраических преобразований.

Признак, по которому производится расчет, может быть выражен абсолютной или относительной величиной. Если признак вы- ражен абсолютной величиной, формула определения необходимого числа наблюдений следующая:

Эти формулы для случайного повторного отбора определяют самый большой объем наблюдений. Определение оптимального объема выборки в комплексных социально-гигиенических исследованиях затруднено тем обстоятельством, что единицы исследуемых совокупностей характеризуются множеством учетных признаков (трудность), так как изучается комплекс показателей здоровья различных групп населения и комплекс факторов, на них воздейству- ющих. Существующие формулы для расчета необходимого числа наблюдений основываются на конкретном единственном признаке. Вести расчет по всем исследуемым признакам невозможно.

Исследователи выделяют основной или результирующий признак и по нему рассчитывают необходимый объем наблюдений.

В ходе анализа собранного материала определяются различные параметры, характеризующие исследуемую совокупность. Это разные параметры с разной вариабельностью. Исследователи определяют их репрезентативность при одном и том же числе единиц наблюдения.

О вариабельности (G, pq) данного признака в генеральной совокупности исследователь судит по данным литературы, если они есть. При отсутствии данных литературы, если признак выражен абсолютным числом, то G определяется по данным пробного исследования, объем которого обычно составляет 30-70 единиц наблюдения. Если признак выражен относительным числом, то пробное исследование, как правило, не проводится, так как проценты вычислять не рекомендуется при числе наблюдений менее 100. В таком случае берут максимальное значение pq=0,25 (p=q=0,5) или pq=2500% (p=q=50%).

Степень уверенности в заданной неточности результата в социально-гигиенических исследованиях обычно составляет 0,95 (t=2).

Другая трудность для исследователя состоит в определении доверительного интервала (Δ), т.е. величины расхождения между средним значением признака генеральной и выборочной совокупности (Δ = М_г - М_в). Эта величина выражается в единицах изучаемого признака и характеризует допускаемую неточность искомой величины генеральной совокупности. Она задается самим исследователем в разумных пределах, исходя из сути изучаемого явления. Незначительное увеличение Δ ведет к резкому сокращению необходимого объема выборки, напротив, незначительное уменьшение Δ резко его увеличивает.

Приведем два примера расчета необходимого числа наблюдений для получения достоверного результата.

Пример 1. Сколько семей нужно исследовать, чтобы дать со- циально-гигиеническую характеристику детородной функции молодых женщин? Подобного исследования раньше не проводилось.

За результирующий признак автор взял число беременностей у молодых женщин за 5 лет брака, провел пробное исследование, оп- росив 50 женщин. Получены следующие данные:

М - среднее арифметическое число беременностей у молодых женщин за 5 лет брака составило 2;

G - среднее квадратичное отклонение = 5;

m=0,25; Δ = 0,5 (p=0,95; t=2).

Расчет проведен следующим образом:

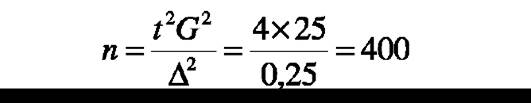
Вывод: для получения статистически достоверных социальногигиенических характеристик детородной функции молодых женщин за 5 лет брака нужно обследовать 400 семей.

Пример 2. Определить, сколько левшей необходимо взять под наблюдение для выявления среди них детей с расстройствами речи.

Доверительная вероятность 95% (0,95). Ошибка показателя не должна превышать 5%. При ранее проводившихся исследованиях расстройств речи у детей дошкольного возраста выявлено, что ими страдают 15% левшей.

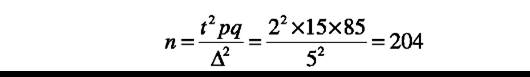
Вывод: для получения статистически достоверных данных о числе детей с расстройствами речи среди левшей нужно обследовать примерно 200 детей-левшей.

Сомнения исследователя в определении основного (результирующего) признака и его неточности (доверительного интервала) при изучении совсем не знакомых совокупностей помогает разрешить следующий прием (Плохинский Н.А., 1961):

Δ и G не определяют заранее, сразу берут ориентировочное отношение Δ/G, которое обозначают К. Это коэффициент точности,

уровень которого выбирает сам исследователь (от 0,5 до 0,1). Примерное необходимое число наблюдений в зависимости от желаемой точности и уверенности в результатах исследования приводится в табл. 43.

Таблица 43. Необходимый объем выборки

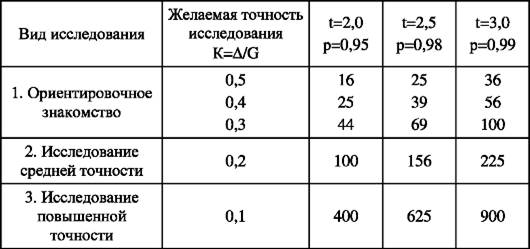
Как видно из табл., необходимый объем выборки для получения устойчивых результатов с достаточной степенью уверенности и точности составляет 400 (К=0,1; р=0,95).

В большинстве комплексных социально-гигиенических исследований на основной ступени исследования по достаточно подробной программе объем выборки составляет 400-800 единиц наблю- дения. Такие исследования вполне надежные и достаточно точные (К=0,1; р=0,95).

Однако в ходе анализа исследуемая совокупность делится на различные группы по разным признакам, репрезентативность которых определяется исследователем. Результирующий признак, положенный в основу расчета статистической совокупности, не является признаком конечной группы анализа. Бывает, что в конечных группах насчитывается лишь несколько единиц наблюдения, и параметры, их характеризующие, могут оказаться недостоверными.

Необходимое число единиц наблюдения для получения устойчивого результата при минимальной точности и достоверности со- ставляет 16-25 (К=0,4; 0,5; р=0,95).

Корреляция признаков

Пятое свойство статистической совокупности - взаимосвязь (корреляция) признаков. В природе и обществе все процессы и явления взаимно связаны. Количественные связи проявляются в функциональной и корреляционной формах.

Функциональная связь: каждому значению одного признака соответствует строго определенное значение другого признака (характерна для физико-химических явлений).

Корреляционная связь: каждому значению одного признака соответствует несколько значений другого признака (характерна для социально-гигиенических и медико-биологических процессов). Корреляционная связь проявляется лишь при массовом сопоставлении признаков в качественно однородной совокупности.

Признаки могут быть качественными и количественными несгруппированными величинами (абсолютными и производными). Задача специалиста - найти причинные связи, подтверждающие зависимость одного явления от другого или от какой-то общей причины.

Корреляция может быть представлена в виде таблиц, графика или коэффициента корреляции.

Коэффициент корреляции (r,p) дает представление о направлении (прямая +, обратная -) и силе связи (от 0 до 1): 0 - связь отсутствует; 0-0,3 - связь слабая; 0,3-0,7 - связь средняя; 0,7-1,0 - связь сильная.

Обычный, наиболее точный и часто применяемый метод (коэффициент) Пирсона:

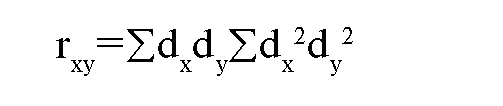
Пример вычисления

d_x и d_y - отклонение каждой варианты ряда «х» и «у» от их средней М.

Более грубый, приближенный и простой ранговый метод Спирмена:

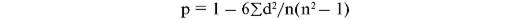
Пример вычисления

d - разность рангов; 6 - постоянный коэффициент; n - число наблюдений (сравниваемых пар).

Рангами - номерами по порядку обозначают признаки. Если признаки одинаковы, всем дается один номер - среднее суммы ран- гов этих признаков. Метод рангов применяют, если число наблюдений меньше 30; если признаки имеют не только количественное, но и качественное выражение; если ряды распределения имеют открытые варианты.

Коэффициент корреляции достоверен, если