Две плоскости пересекаются по прямой линии. Когда одна плоскость является проецирующей, задача упрощается. Находим две точки линии пересечения, которые принадлежат одновременно двум плоскостям. Строим линию l пересечения фронтально проецирующей плоскости ∆(∆2) с плоскостью ∑(А,В,С)(рисунок 2.37).
Фронтальная проекция l2 линии пересечения l будет совпадать с вырожденной проекцией плоскости ∆(∆2) т. е. ∆2 = l2.
Горизонтальная проекция l1 искомой линии l строится по принадлежности этой линии плоскости ∑ (A,B,С).

18) Построение точки пересечения прямой с плоскостью общего положения (рис. 226, а) выполняют с помощью вспомогательной проецирующей плоскости R, которую проводят через данную прямую EF. Строят линию пересечения 12 вспомогательной плоскости R с заданной плоскостью треугольника ABC, получают в плоскости R две прямые: EF — заданная прямая и 12 — построенная линия пересечения, которые пересекаются в точке К.

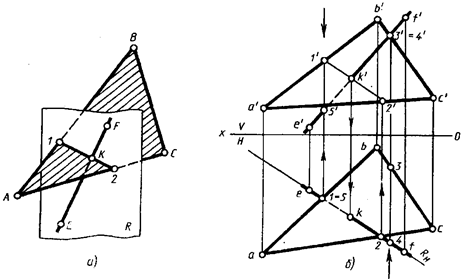
Рис. 226

Нахождение проекций точки К показано на рис. 226,б. Построения выполняют в следующей последовательности.

Через прямую EF проводят вспомогательную горизонтально-проецирующую плоскость R. Ее след R_H совпадает с горизонтальной проекцией ef прямой EF.

Строят фронтальную проекцию 1'2' линии пересечения 12 плоскости R с заданной плоскостью треугольника ABC с помощью линий проекционной связи, так как горизонтальная проекция линии пересечения известна. Она совпадает с горизонтальным следом R_H плоскости R.

Определяют фронтальную проекцию k' искомой точки К, которая находится в пересечении фронтальной проекции данной прямой с проекцией 1'2' линии пересечения. Горизонтальная проекция точки строится с помощью линии проекционной связи.

Видимость прямой относительно плоскости треугольника ABC определяется способом конкурирующих точек. Для определения видимости прямой на фронтальной плоскости проекций (рис. 226,б) сравним координаты Y точек 3 и 4, фронтальные проекции которых совпадают. Координата Y точки 3, лежащей на прямой ВС, меньше координаты Y точки 4, лежащей на прямой EF. Следовательно, точка 4 находится ближе к наблюдателю (направление взгляда указано стрелкой) и проекция прямой изображается на плоскости V видимой. Прямая проходит перед треугольником. Левее точки К' прямая закрыта плоскостью треугольника ABC.

Видимость на горизонтальной плоскости проекций показывают, сравнив координаты Z точек 1 и 5. Так как Z₁ > Z₅, точка 1 видимая. Следовательно, правее точки 1 (до точки К) прямая EF невидимая.

19)Пересечение плоскостей общего положения
Линия пересечения двух плоскостей – это прямая, одновременно принадлежащая обеим плоскостям. Для ее определения достаточно найти две общие для заданных плоскостей точки.

На рис. 73 изображены две пересекающиеся плоскости b и a. Для нахождения линии пересечения К₁К₂:

а) пересекаем обе заданные плоскости вспомогательными секущими плоскостями ₁g и g₂;

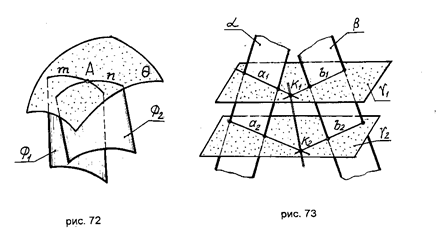
б) строим линии пересечения а₁ и b₁, а₂и b₂ соответственно с плоскостями g₁ и g₂ плоскостей g₁ и g₂.
в) находим точки К₁и К₂:

К₁= а₁Ç b₁, К₂= а₂Ç b₂.

Полученные точки К₁и К₂ определяют линию пересечения заданных плоскостей К₁К₂ .

20)Параллельные плоскости
 Две плоскости называются параллельными, если они не пересекаются.
Признак параллельности двух плоскостей- если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Свойства параллельных прямых:
●Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
● Отрезки параллельных прямых, заключённые между параллельными плоскостями равны.
● Если прямая пересекает плоскость, то она пересекает также любую плоскость параллельную данной.
● Если плоскость пересекает одну из параллельных плоскостей, то она пересекает и другую.
● Через точку не лежащую в данной плоскости проходит плоскость параллельная данной и притом только одна.
● Если две плоскости параллельны третьей, то они параллельны между собой.

21) Вращение вокруг проецирующей
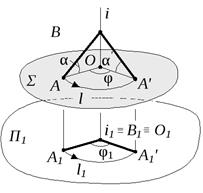
Рассмотрим механизм вращения вокруг проецирующей оси на примере отрезка прямой (АВ). Пусть ось вращения i, проведенная через точку В, перпендикулярна, например, горизонтальной плоскости проекцийΠ1 (рис. 32,а). В этом случае точка В, как и любая другая точка, принадлежащая оси, неподвижна, а точка А заданной прямой совершает вращательное движение в плоскости Σ. Повернувшись на некоторый угол φ, точка А займет положение А'. При этом очевидно, что величина угла наклона прямой АВ к горизонтальной плоскости проекций не изменит своей величины, т. е. α' = α. Отсюда вытекает основное свойство проекций при вращении вокруг проецирующей оси. Соответствующая проекция не меняет своей формы и размеров. В приведенном на рис. 32,апримере, такой проекцией является горизонтальная проекцияА1В1отрезкаАВ, т. е.А1В1 =А1'В1.

22) Определение натуральной величины прямой общего положения
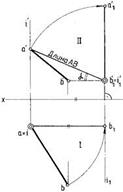
Проводим ось вращения i (i1,i2) перпендикулярноπ1 через точку В(B1B2) прямой l (l1,l2). При вращении прямой l вокруг оси i точка В прямой останется неподвижной, так как принадлежит оси,

А точка А будет вращаться по правилам, рассмотренным выше. Точку А поворачиваем относительно оси i на угол α, прямая l в этом случае займет положение, параллельное плоскостиπ2,

А следовательно, спроецируется на эту плоскость в натуральную величину

(A2 B2). Одновременно в натуральную величину проецируется угол наклона отрезка АВ к плоскости π1.

23) Преобразование прямой общего положения в проецирующую
Сущность способа вращения заключается в том, что при неизменном положении основных плоскостей проекций изменяется положение заданных геометрических элементов относительно плоскостей проекций путем их вращения вокруг некоторой оси до тех пор, пока эти элементы не займут частное положение в исходной системе плоскостей.
Способ вращения вокруг оси, перпендикулярной плоскости проекции, применим для перемещения отрезка прямой общего положения в частное.
Преобразования, аналогичные тем, которые выполнялись способом замены плоскостей проекций, производятся и при определении вращением действи­тельной величины плоской фигуры.

24)Определение натуральной величины плоскости общего положения методом плоскопараллельного перемещения
Задача Определить натуральную величину плоскости общего положения, заданную треугольником АВС, способом плоскопараллельного перемещения.

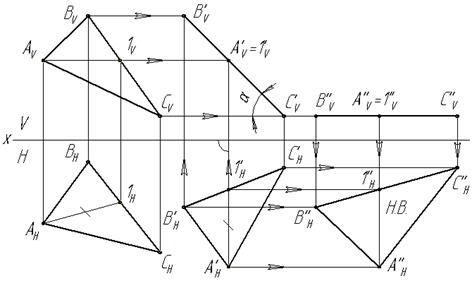Алгоритм решения задачи

1 Провести горизонталь А1 в треугольнике АВС.

2 Горизонталь А’H1’H построить перпендикулярно фронтальной плоскости на произвольном расстоянии от нее.

3 Методом засечек относительно горизонтали А’Н1’Н перенести горизонтальную проекцию треугольника в положение А’НВ’НС’Н(АНВНСН = =А’НВ’НС’Н). По горизонтальной проекции треугольника построить его фронтальную проекцию. При этом перемещении плоскость общего положения преобразовали во фронтально-проецирующую плоскость.

4 Перенести новую фронтальную проекцию треугольника А’VВ’VC’Vв положение А’’VВ’’VС’’V, параллельное горизонтальной плоскости проекций (плоскость уровня), достроить горизонтальную проекцию А’’НВ’’НС’’Н. Горизонтальная проекция А’’НВ’’НС’’Н будет являться натуральной величиной треугольника АВС(рисунок 4).

25) Преобразование плоскости общего положения в проецирующую + определение угла наклона к плоскостям проекций методом плоскопараллельного перемещения
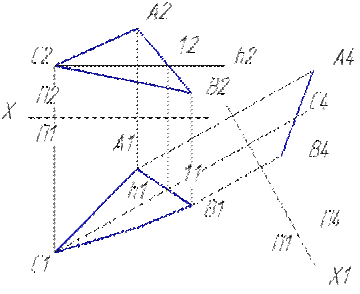
Пусть дана плоскость общего положения, заданная двумя пересекающимися прямыми. Эти прямые в вариантах заданы тремя точками. Соединив эти точки между собой, получим плоскость треугольника АВС.

1.Проведем в плоскости одну из главных линий – горизонталь или фронталь. Это построение необходимо для выбора новой оси проекций, так как у проецирующих плоскостей одна из главных линий является прямой проецирующей, т.е. одна ее проекция располагается перпендикулярно оси проекций, а вторая проекция является точкой.
На рисунке 5 проведена горизонталь плоскости h.
2. Проводим новую ось проекций перпендикулярно горизонтальной проекции горизонтали Х 1.
3. Затем строим новые проекции точек на плоскость П4, как это было показано ранее. Если построение проведено верно, то проекцией плоскости на плоскость П4 будет прямая, т.е. плоскость общего положения стала перпендикулярна плоскости проекций П4, что и являлось целью данного преобразования.

26) Проецирование многогранной поверхности
 Аксонометрические проекции многогранников, так же как и многоугольников, строятся при помощи координат вершин многогранника.
Грани призм, пирамид, которые перпендикулярны к плоскостям проекций, проецируются на    них в виде отрез­ков прямых линий.

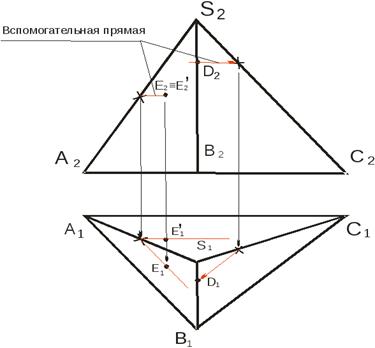
Точка на поверхности многогранника.
При построении проекций точек на поверхности (ребре или грани) многогранника необходимо следовать аксиомам принадлежности (принадлежность точке прямой и принадлежность точки плоскости). Проекции точек должны принадлежать соответствующим проекциям ребер. На рис.3 построены проекции точки D, принадлежащей профильному ребру SB боковой поверхности пирамиды. Проекция точки D2 задана, для построения проекции D1 используется вспомогательная прямая, которая параллельна ребру основания ВС.
Точка Е принадлежит боковой поверхности пирамиды (Е2 задана). По фронтальной проекции нельзя точно сказать, какой грани ASB или АSС, принадлежит точка, поэтому будем рассматривать две конкурирующие точки Е и Е/. Для построения второй проекции точки Е (Е1) проводятся вспомогательные прямые, параллельные ребрам основания АС и АВ.

27)Пересечение многогранника частного положения с плоскостью общего положения
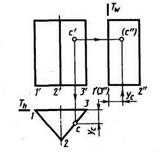
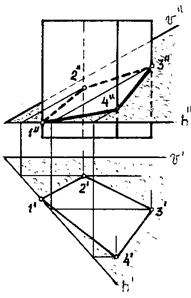
На рисунке показано сечение прямой четырехугольной призмы плоскостью общего положения. Секущая плоскость задана двумя пересекающимися прямыми — горизонталью и фронталью. Боковые грани призмы — горизонтально-проецирующие плоскости. Следовательно, горизонтальная проекция сечения известна, она совпадает с горизонтальной проекцией боковых граней и ребер призмы.
Для построения фронтальной проекции сечения необходимо спроецировать точки 1', 2', 3' и 4', принадлежащие секущей плоскости, на фронтальную проекцию. Воспользуемся какой-либо линией уровня, например фронталью. Проводим через точки 1', 2', 3' и 4' горизонтальные проекции фронталей, а затем строим их фронтальные проекции. В пересечении с соответствующими фронтальными проекциями ребер получим искомые проекции точек пересечения ребер с плоскостью. Соединив полученные точки прямыми в последовательности, которая задана горизонтальной проекцией и определив невидимые участки сечения, закончим построение.

28) Пересечение многогранника с прямой (частные случаи)
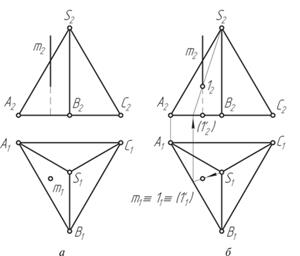
На рис. 106 задана пирамида SABC и горизонтально проецирующая прямая т. Требуется построить проекции точек пересечения прямой с многогранником.

Так как прямая является горизонтально проецирующей, то из определения следует, что все проекции точек, лежащих на прямой, будут совпадать на горизонтальной плоскости проекций. Из рис. 106 видно, что прямая пересекает грань пирамиды SAB и основание. Проекции точек пересечения прямой с пирамидой будут совпадать на горизонтальной плоскости с проекцией самой прямой. В шестом параграфе были рассмотрены примеры построения точки, принадлежащей пирамиде, по одной ее проекции. После построения точек пересечения прямой многогранника (рис. 106, б) находим видимость прямой.

29) Пересечение многогранника плоскостью частного положения
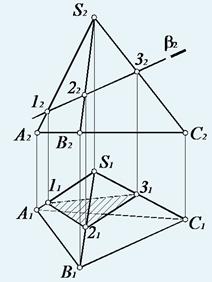
При пересечении многогранной поверхности с плоскостью получается ломаная линия. Для ее построения достаточно определить точки пересечения ребер многогранника и секущей плоскости и соединить построенные точки с учетом их видимости. Секущая плоскость β(β2) занимает фронтально проецирующее положение, поэтому точки пересечения ребер определяются как точки пересечения прямой общего положения и плоскости частного положения.

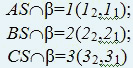
Видимость определяется методом конкурирующих точек. Грань ACS относительно плоскости П1 невидима, следовательно, и линия (11–31) также невидима. Видимость на П2, в данном случае, не определяется.

30) Пересечение многогранной поверхности прямой (общий случай)
Если многогранник выпуклый, то существует только две точки пересечения прямой с многогранной поверхностью. Рассмотрим общий алгоритм решения этой задачи на следующем примере. Дана трехгранная призма и прямая а — общего положения. Требуется найти точки пересечения M и N.
Заключаем прямую a во вспомогательную плоскость s: a 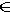s.

1. 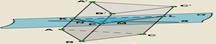Плоскость s пересекает многогранник по ломаной KLP.

2. Ломаная KLP пересекается с прямой a в точках N и M. Точки N и M — искомые точки пересечения прямой a с многогранником.

Выбор положения вспомогательной плоскости s осуществляется, исходя из точности и простоты построений. Теперь рассмотрим на чертеже пример построения точек пересечения прямой а общего положения с трехгранной призмой ABCA'B'C' (рис. 6.8). Для этого через прямую а проведем фронтально проецирующую плоскость s: а 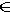s.

Алгоритм построения:

1. Через a2 вводим вспомогательную проецирующую плоскость s 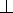П2, a2 = s2

2. Отмечаем проекции K2, P2, L2 точек K, P,L, где K 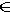AA', P 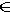BB', L 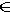CC'.

3. Из условия принадлежности определяем их первые проекции K1, P1,L1.

4. При пересечении a1 с треугольникомK1P1L1 получаем горизонтальные проекции N1 и M1 точек пересечения N иM прямой a с поверхностью призмы.

5. Находим точки N2 и M2: N2 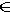a2, M2 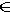a2 с помощью линий связи. Точки N2 и M2 — вторые проекции искомых точек пересечения прямой а с поверхностью призмы.

6. Определяем видимость прямой с помощью метода конкурирующих точек.

31) Взаимное пересечение многогранников
Линию пересечения двух многогранников можно построить двумя способами:
- найдя точки пересечения ребер каждой поверхности с гранями другой поверхности и соединив их в определенной последовательности;
- построив линии пересечения граней одного многогранника с гранями другого. Преимущество отдается тому из способов, который в зависимости от условий задания многогранников дает более простое решение. Линиями пересечения многогранников в общем случае являются пространственные замкнутые многоугольники.
В зависимости от вида многогранников и их взаимного расположения линиями пересечения могут быть один, два и более многоугольников.
Следует иметь в виду, что стороны этих многоугольников будут видимыми, если они являются результатом пересечения видимых граней, если хотя бы одна из пересекающихся граней невидимая (сторона многоугольника), то линия их пересечения - невидимая.
Заданы пересекающиеся призма АВС и пирамида SDEG. Построить проекции линии пересечения.
Грани призмы - горизонтально проецирующие плоскости, поэтому горизонтальные проекции фигуры сечения будут совпадать с горизонтальной проекцией призмы. Учитывая это, целесообразно применить первый способ решения задачи. Отметим горизонтальные проекции 2', 3', 5', б' точек пересечения ребер пирамиды с призмой, определим их фронтальные проекции.
Для определения точек пересечения ребра В призмы с пирамидой через ребро В и вершину S проведена горизонтально-проецирующая плоскость α, которая пересекает пирамиду по треугольнику S-7-8.
На пересечении фронтальных проекций S"7", S"8" и ребра В" отмечены точки 1" и 4". Полученные точки на одних и тех же гранях соединены отрезками прямых. В сечении получен пространственный многоугольник 1, 2, 3, 4, 5, 6, 1. С учетом изложенного выше правила отмечены видимые и невидимые стороны многоугольника.

32) Способы построения разверток многогранников (нормальное сечение)
Для получения развертки многогранной поверхности необходимо разрезать ее по некоторым ребрам и последовательно совместить все ее грани с одной плоскостью так, чтобы образовалась связная фигура. Для одной и той же фигуры вид поверхности развертки может быть различным в зависимости от избранной последовательности в расположении граней на развертке. Все грани на развертке изображаются в натуральную величину, поэтому построение развертки сводится к определению натуральных величин отдельных граней поверхности.
Способ нормального сечения применяется для развертки призматических гранных поверхностей. Отличительная особенность данного способа является построение сечения призмы плоскостью нормальной (перпендикулярной) по отношению к ее боковым ребрам. При последующем развертывании призмы линия нормального сечения выстраивается в прямую линию и используется для откладывания от нее натуральной величины отрезков боковых ребер. Построим развертку наклонной трехгранной призмы ABCDEF, иcпользуя способ нормального сечения.
Построим сечение заданной призмы вспомогательной плоскостью γH перпендикулярной к ее боковым ребрам и горизонтальной плоскости проекций H. Методом перемены плоскостей проекций определяем действительную величину сторон Δ123. В произвольном месте эпюра проводим горизонтально прямую a. От точки 10, отмеченной на этой прямой, откладываем отрезки [1020], [2030], [3010], конгруентные сторонам Δ123. Через точки 102030 и 10 проводим прямые перпендикулярные к прямой a, и откладываем на них от точек 102030 и 10 отрезки, конгруентные соответствующим действительным величинам отрезков боковых ребер. Полученные точки A0B0C0A и D0E0 F0D0 соединяем прямыми. Ребра AD, BE, и CF параллельны плоскости H, поэтому на нее они проецируются в действительную величину. Плоская фигура A0B0C0A0D0E0F0D0 - развертка боковой поверхности призмы. К ней пристроены основания призмы ΔA0B0C0 и ΔD0E0F0.

33) Построение развертки пирамиды
В качестве примера рассмотрим построение полной развертки поверхности трехгранной пирамиды SАВС (рис. 9.1).
Вначале построим основание пирамиды, натуральную величину А111 которого определим методом вращения вокруг проецируемой прямой i. Величину боковых ребер SA, SB и SC можно определить вращением вокруг проецируемой прямой j. Отрезки S2А2’, S2В2’ и S2С2’ равны длинам соответствующих боковых ребер заданной пирамиды.
Построение развертки можно провести в следующем порядке:
1)Построить ∆ А0В0С0 = ∆ А111.
2)На каждом из ребер основания построить боковые грани, использую найденные натуральные величины боковых ребер S2А2’, S2В2’ и S2С2’пирамиды.
Полученная плоская фигура является разверткой поверхности данной пирамиды.

34) Способ замены плоскостей проекций
Способы преобразования комплексного чертежа разделяют на две группы по признаку, определяющему положение фигуры и плоскостей проекций друг относительно друга или направление проецирования:
1. Изменяют положение плоскостей проекций или направление проецирования так, чтобы неподвижная в пространстве фигура оказалась в частном положении. К этой группе относят способ замены плоскостей проекций и способ дополнительного проецирования.
2. Изменяют положение геометрической фигуры в пространстве так, чтобы она оказалась в частном положении относительно фиксированной системы плоскостей проекций. В эту группу включают способ плоскопараллельного перемещения и способ вращения.
Сущность способа замены плоскостей проекций состоит в замене первоначальной системы взаимно перпендикулярных плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций при неизменном положении геометрической фигуры в пространстве.

Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П4 проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

35) Определение истинной величины отрезка прямой общего положения
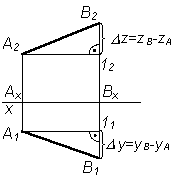
Для определения натуральной величины отрезка прямой линии общего положения по ее проекциям применяют метод прямоугольного треугольника.

Определить на комплексном чертеже Аz, Bz, Ay, By: D z – разность расстояний от точек А и В до плоскости p1; D y – разность расстояний от точек А и В до плоскости p2
Взять любую точку проекции прямой АВ, провести через нее перпендикуляр к отрезку: а) либо перпендикуляр к А2В2 через точку В2 или А2; б) либо перпендикуляр к А1В1 через точку В1 или А1

На этом перпендикуляре от точки В2 yDотложить или от точки B1 zDотложить
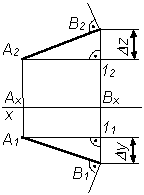
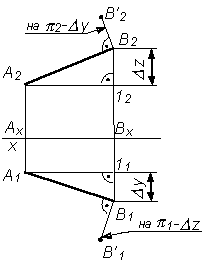
4. Соединить A2 и В'2; A1 и В'1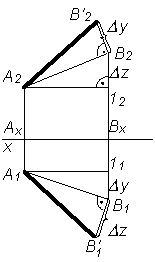
5. Обозначить натуральную величину отрезка АВ (гипотенузу треугольника): |АВ| = А1В'1 = А2В'2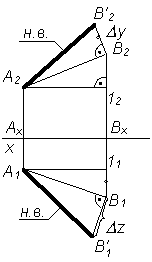

36) Способ замены плоскостей проекции
см №34

37) Определение расстояния между параллельными прямыми
Параллельные плоскости α и β расположены так, как показано на рисунке.
Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на плоскости  α, опустить перпендикуляр AB на плоскости β и определить его настоящую длину.
Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций.
Вспомогательная точка M используется для определения направления следов f0β1 и f0α1, параллельных друг другу.

38) Определение истинной величины плоскости общего положения способом замены плоскостей проекций
Определить натуральную величину треугольника АВС способом замены плоскостей проекций.
 Проведем в плоскости треугольника АВС фронталь f (линия С-1), а затем, заменяя π1, введем новую плоскость проекций π3, проходящую через ось Х1 и перпендикулярную к фронтальной проекции фронтали f" (С"-I"). На π3заданная плоскость треугольника АВС спроецируется в прямую линию, т.е., станет проецирующей по отношению к этой плоскости проекций;

Второй заменой плоскости проекций π2 на новую плоскость проекций π4, проходящую через ось Х2 и параллельную проекции А"′В"′С"′ нашего треугольника, найдем на плоскости π4 натуральную величину треугольника ABС - фигуру А1VВ1VС1V.

39) Способ плоскопараллельного перемещения
Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.
*Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
*Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C'1D'1 = C'D' перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A'1B'1C'1 = A'B'C'. По линиям связи определяем точки A''1, B''1, C''1.
*Перемещаем проекцию A''1B''1C''1 треугольника ABC в положение A''2B''2C''2, параллельное оси X, соблюдая равенство A''2B''2C''2 = A''1B''1C''1. По линиям связи определяем точки A'2, B'2, C'2. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A'2B'2C'2.