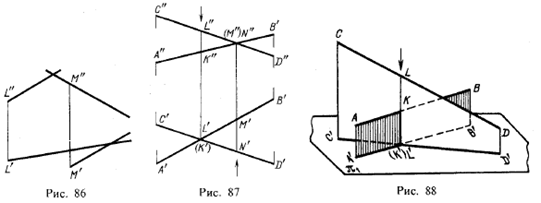
Скрещивающиеся прямые линии не пересекаются и не параллельны между собой. На рис. 86 изображены две скрещивающиеся прямые общего положения: хотя одноименные проекции и пересекаются между собой, но точки их пересечения не могут быть соединены линией связи, параллельной линиям связи L"L' и М"М', т. е. эти прямые не пересекаются между собой.

Как надо рассматривать точку пересечения одноименных проекций скрещивающихся прямых? Она представляет собой проекции двух точек, из которых одна принадлежит первой, а другая — второй из этих скрещивающихся прямых. Например, на рис. 87 точка с проекциями К” и К' принадлежит прямой АВ, а точка с проекциями L" и L' принадлежит прямой CD. Эти точки одинаково удалены от пл. π2, но расстояния их от пл. π1 различны: точка с проекциями L" и L' дальше от π1, чем точка с проекциями К" и К' (рис. 88).

Точки с проекциями М", М' и N”, N' одинаково удалены от пл. π1 но расстояния этих точек от пл. π2 различны.

Точка с проекциями L" и L', принадлежащая прямой CD, закрывает собой точку с проекциями К" и К' прямой АВ по отношению к пл. π1; соответствующее направление взгляда показано стрелкой у проекции L". По отношению к пл. π2 точка с проекциями N" и N' прямой CD закрывает собой точку с проекциями М" и М' прямой АВ; направление взгляда указано стрелкой внизу, у проекции N'.

Обозначения проекций «закрытых» точек помещены в скобках 1).

Точки, расположенные на одной проецирующей прямой, называются конкурирующими. Точки, расположенные на одной горизотально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 64, а), конкурирующих на горизонтальной плоскости проекций, видима та, высота которой больше (B–видима, A– невидима).

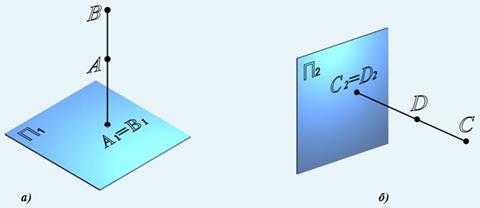
Рис. 64. Конкурирующие точки: а – относительно горизонтальной плоскости проекций; б – относительно фронтальной плоскости проекций

Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 64, б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C – видима, D – невидима). Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 65). .

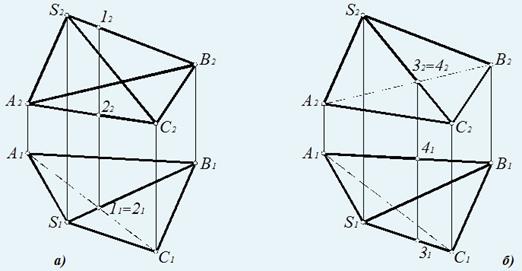
Рис. 65. Определение видимости ребер тетраэдра на комплексном чертеже: а – относительно горизонтальной плоскости проекций; б – относительно фронтальной плоскости проекций

Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 65, а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1∈SB и 2∈AC являются конкурирующими на П1, поскольку находятся на проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1 , следовательно, видимо и ребро SB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABC невидима на П1.

Видимость на фронтальной проекции (рис. 65, б) определяется с помощью конкурирующих точек 3∈SC и 4∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SC на фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы наП2 .