Основные сведения о параллельном проецировании. Свойства.
Параллельное проецирование используется тогда, когда размерное соответствие обязательно, а центр проецирования находится в бесконечности и проецирующие лучи параллельны между собой.
В качестве фиксированного базиса используют три взаимно-перпендикулярных плоскости проекции:
1. Фронтальная(V). Она стационарная. Проекциям точек этой плоскости присваивается индекс этой плоскости, например, Av, Aн, Aw
2. Горизонтальная(Н). Для получения плоского чертежа ее поворачивают относительно оси ОХ (переднюю полу вниз, заднюю вверх)
3. Профильная(W). Расположена как и первая вертикально, но перпендикулярна к фронтальной , и разворачивается против часовой стрелки вокруг оси OZ при совмещении плоскости в единую.
Эти три плоскости взаимно перпендикулярны и имеют 8 углов – октантов.
Пересекаясь между собой, они образуют линии пересечения – оси.
V и H – OX (ось абсцисс)
H и W – OY (ось ординат)
V и W- OZ (ось аппликат)
Проецирующие лучи параллельны между собой и перпендикулярны к плоскостям проекции.
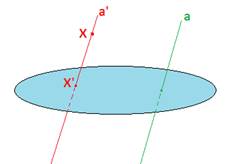
X’ – параллельная проекция точки Х на плоскость.
Плоскость называют плоскостью проекции, а прямая а задает направление проектирования
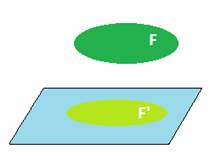
Проекцией фигуры F является множество F’ проекций всех ее точек. Отображение, сопоставляющее каждой точки Х фигуры F ее параллельную проекцию – точку X’ фигуры F’, называется параллельным проектированием фигур.
Параллельная проекция реального предмета – его тень.
Теорема: При параллельном проектировании для прямых, не параллельных направлению проектирования, и для лежащих на них отрезков выполняются следующие свойства:
- Проекция прямой – есть прямая, а отрезка – отрезок.
- Проекция параллельных прямых параллельны или совпадают
- Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, ровно отношению длин самих отрезков.
При параллельном проектировании середина отрезка проектируется в середину его проекции.
При проецировании необходимо соблюдать эти свойства, но в остальном оно может быть произвольном. Углы и отношение длин непараллельных отрезков могут изменяться произвольно Но если треугольник равносторонний, то на проекции его медиана должна соединять вершину треугольника с серединой противоположной стороны.
Прямые линии частного положения. Прямые уровня.
Прямая частного положения – прямая, параллельная хотя бы к одной из плоскостей проекций.
Условно частные положения прямых можно разбить на три группы.
Первая группа
Прямые параллельные двум плоскостям проекций и перпендикулярные к третьей.
Горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций
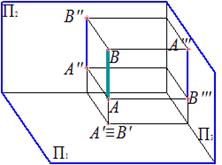
|
Фронтально проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций
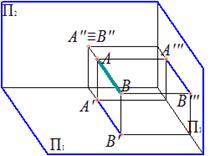
|
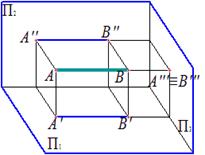
Профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций
|
Вторая группа
Прямые параллельны одной плоскости проекций, а к двум другим направлены под углом.
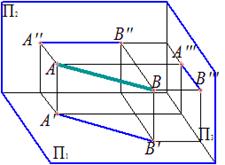
Горизонтальная прямая – прямая, параллельная горизонтальной плоскости проекций
|
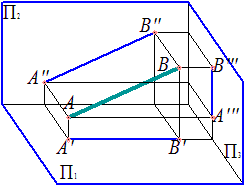
Фронтальная прямая – прямая, параллельная фронтальной плоскости проекций
|
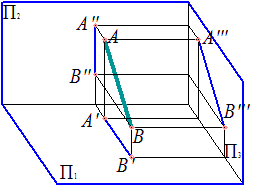
Профильная прямая – прямая, параллельная профильной плоскости проекций
|
Третья группа
Прямые, лежащие в плоскостях проекций
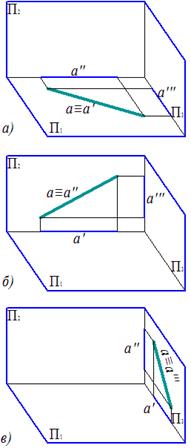 а) в горизонтальной; б) в фронтальной; в) в профильной а) в горизонтальной; б) в фронтальной; в) в профильной
|
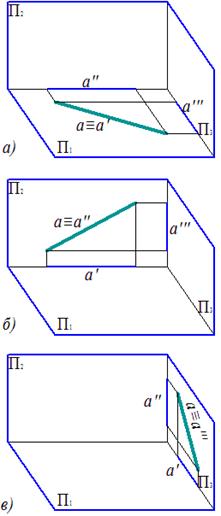
Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.
Исходя из положения прямых уровня в пространстве, их проекции выглядят как показано на рис. 2.1.
а)Прямая, параллельная горизонтальной плоскости проекций П1, называется горизонтальной прямой уровня или горизонталью и обозначается h.
б) Прямая, параллельная фронтальной плоскости проекций П2, называется фронтальной прямой уровня или фронталью и обозначается f.
в) Прямая, параллельная профильной плоскости проекций П3, называется профильной линией уровня и обозначается p.
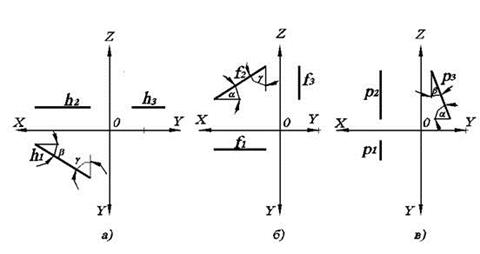
Горизонталь характерна тем, что ее фронтальная проекция параллельна оси ОХ. Фронталь характерна тем, что ее горизонтальная проекция параллельна оси ОХ.
Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без искажений). Поэтому h1, f2, p3 – это натуральная величина соответствующих прямых h, f, p.
Первая группа
Прямые параллельные двум плоскостям проекций и перпендикулярные к третьей.
Горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций
|
Фронтально проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций
|
Профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций
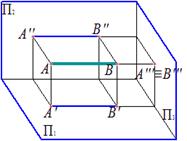
|
Вторая группа
Прямые параллельны одной плоскости проекций, а к двум другим направлены под углом.
Горизонтальная прямая – прямая, параллельная горизонтальной плоскости проекций
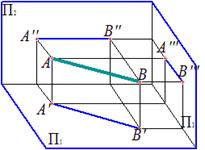
|
Фронтальная прямая – прямая, параллельная фронтальной плоскости проекций
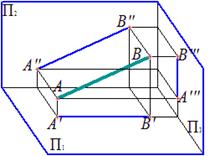
|
Профильная прямая – прямая, параллельная профильной плоскости проекций
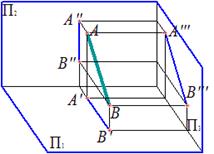
|
Третья группа
Прямые, лежащие в плоскостях проекций
 а) в горизонтальной; б) в фронтальной; в) в профильной а) в горизонтальной; б) в фронтальной; в) в профильной
|
Рис. 64. Конкурирующие точки: а – относительно горизонтальной плоскости проекций; б – относительно фронтальной плоскости проекций
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 64, б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C – видима, D – невидима). Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 65). .
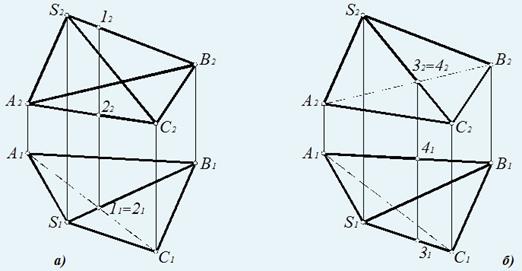
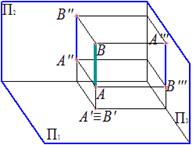
Рис. 65. Определение видимости ребер тетраэдра на комплексном чертеже: а – относительно горизонтальной плоскости проекций; б – относительно фронтальной плоскости проекций
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 65, а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1∈SB и 2∈AC являются конкурирующими на П1, поскольку находятся на проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1 , следовательно, видимо и ребро SB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABC невидима на П1.
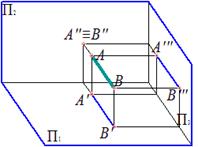
Видимость на фронтальной проекции (рис. 65, б) определяется с помощью конкурирующих точек 3∈SC и 4∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SC на фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы наП2 .
Главные линии плоскости.
Кроме прямых общего положения в плоскости можно выделить линии частного положения, которые называют главными линиями плоскости – это линии уровня и линии наклона плоскости.
1. Горизонтали плоскости h – прямые, принадлежащие плоскости и параллельные плоскости p1 (рис. 4.6).
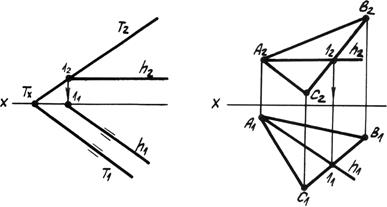
Рис. 4.6. Горизонтали плоскости.
На эпюре фронтальная проекция горизонтали h2 параллельна оси x, а горизонтальная проекция горизонтали h1 параллельна горизонтальному следу плоскости h1 || Т1, т.е. горизонтальный след плоскости – это тоже её горизонталь.
2. Фронтали плоскости ¦ – прямые, принадлежащие плоскости и параллельные плоскости p2 (рис. 4.7).
На эпюре горизонтальная проекция фронтали ¦1 параллельна оси x1, а фронтальная проекция фронтали параллельна фронтальному следу плоскости ¦2 || Г2, т.е. фронтальный след плоскости – это тоже фронталь плоскости.
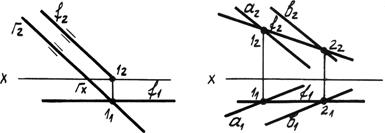
Рис. 4.7. Фронтали плоскости.
3. Профильные прямые плоскости p – прямые, принадлежащие плоскости и параллельные плоскости p3 (рис. 4.8).
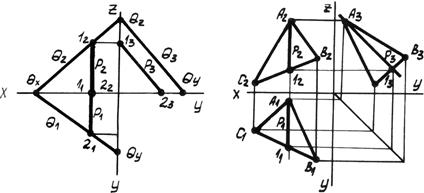
Рис. 4.8. Профильные прямые плоскости.
На эпюре горизонтальная и фронтальная проекции профильной прямой р1 и р2 перпендикулярны оси x, а профильная проекция профильной прямой р3 параллельна профильному следу р3 || q3, т.е. профильный след плоскости – это тоже её профильная прямая.
4. Линия наибольшего наклона плоскости l – это прямая, принадлежащая плоскости и перпендикулярная к соответствующей линии уровня плоскости. С помощью линии наибольшего наклона определяется угол наибольшего наклона плоскости к соответствующей плоскости проекции.
Линия l, перпендикулярная горизонтальной плоскости, определяет угол наклона плоскости к плоскости p1 (рис. 4.9).
Если плоскость задана следами, то горизонтальная проекция линии наибольшего наклона плоскости перпендикулярна горизонтальному следу l1 (рис. 4.9). Если плоскость задана другим способом, необходимо построить горизонталь плоскости, тогда горизонтальная проекция линии наибольшего наклона определяется перпендикулярно горизонтальной проекции горизонтали, l1 ^ h1.
Основные сведения о параллельном проецировании. Свойства.
Параллельное проецирование используется тогда, когда размерное соответствие обязательно, а центр проецирования находится в бесконечности и проецирующие лучи параллельны между собой.
В качестве фиксированного базиса используют три взаимно-перпендикулярных плоскости проекции:
1. Фронтальная(V). Она стационарная. Проекциям точек этой плоскости присваивается индекс этой плоскости, например, Av, Aн, Aw
2. Горизонтальная(Н). Для получения плоского чертежа ее поворачивают относительно оси ОХ (переднюю полу вниз, заднюю вверх)
3. Профильная(W). Расположена как и первая вертикально, но перпендикулярна к фронтальной , и разворачивается против часовой стрелки вокруг оси OZ при совмещении плоскости в единую.
Эти три плоскости взаимно перпендикулярны и имеют 8 углов – октантов.
Пересекаясь между собой, они образуют линии пересечения – оси.
V и H – OX (ось абсцисс)
H и W – OY (ось ординат)
V и W- OZ (ось аппликат)
Проецирующие лучи параллельны между собой и перпендикулярны к плоскостям проекции.

X’ – параллельная проекция точки Х на плоскость.
Плоскость называют плоскостью проекции, а прямая а задает направление проектирования

Проекцией фигуры F является множество F’ проекций всех ее точек. Отображение, сопоставляющее каждой точки Х фигуры F ее параллельную проекцию – точку X’ фигуры F’, называется параллельным проектированием фигур.
Параллельная проекция реального предмета – его тень.
Теорема: При параллельном проектировании для прямых, не параллельных направлению проектирования, и для лежащих на них отрезков выполняются следующие свойства:
- Проекция прямой – есть прямая, а отрезка – отрезок.
- Проекция параллельных прямых параллельны или совпадают
- Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, ровно отношению длин самих отрезков.
При параллельном проектировании середина отрезка проектируется в середину его проекции.
При проецировании необходимо соблюдать эти свойства, но в остальном оно может быть произвольном. Углы и отношение длин непараллельных отрезков могут изменяться произвольно Но если треугольник равносторонний, то на проекции его медиана должна соединять вершину треугольника с серединой противоположной стороны.
Дата: 2018-12-28, просмотров: 817.