Прямая линия в пространстве определяется положением двух ее точек, например А и В, достаточно выполнить комплексный чертеж этих двух точек, затем соединить одноименные проекции, получим соответственно горизонтальную, фронтальную и профильную проекции прямой.

Проекция прямой – всегда прямая, кроме тех случаев, когда прямая перпендикулярна к одной из плоскостей, и проекция этой прямой на эту плоскость будет изображаться в виде точки.

Чтобы положение прямой в пространстве было определенным, необходимо иметь не менее двух проекций отрезка

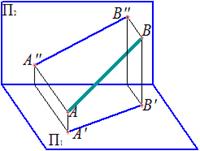
Прямая общего положения - это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций. Она пересекает все три плоскости проекций. Точку пересечения (встречи) прямой с плоскостью проекции называют следом прямой.

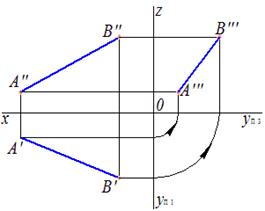
Прямые линии частного положения. Прямые уровня.

Прямая частного положения – прямая, параллельная хотя бы к одной из плоскостей проекций.

Условно частные положения прямых можно разбить на три группы.

Первая группа

Прямые параллельные двум плоскостям проекций и перпендикулярные к третьей.

Горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций

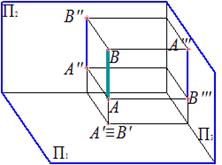
Фронтально проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций

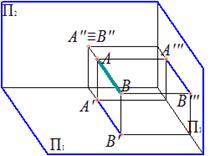
Профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций

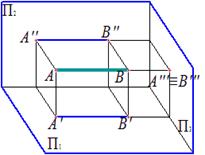
Вторая группа

Прямые параллельны одной плоскости проекций, а к двум другим направлены под углом.

Горизонтальная прямая – прямая, параллельная горизонтальной плоскости проекций

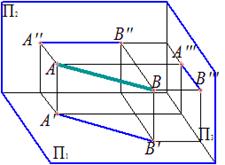
Фронтальная прямая – прямая, параллельная фронтальной плоскости проекций

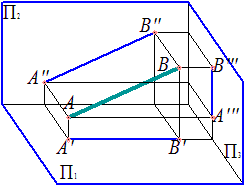
Профильная прямая – прямая, параллельная профильной плоскости проекций

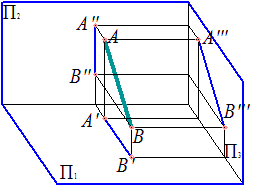
Третья группа

Прямые, лежащие в плоскостях проекций

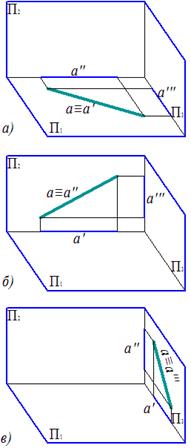а) в горизонтальной; б) в фронтальной; в) в профильной

Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.

Исходя из положения прямых уровня в пространстве, их проекции выглядят как показано на рис. 2.1.

а)Прямая, параллельная горизонтальной плоскости проекций П1, называется горизонтальной прямой уровня или горизонталью и обозначается h.

б) Прямая, параллельная фронтальной плоскости проекций П2, называется фронтальной прямой уровня или фронталью и обозначается f.

в) Прямая, параллельная профильной плоскости проекций П3, называется профильной линией уровня и обозначается p.

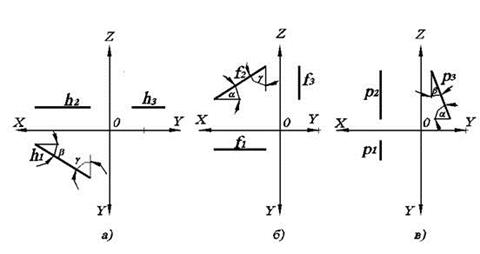
Горизонталь характерна тем, что ее фронтальная проекция параллельна оси ОХ. Фронталь характерна тем, что ее горизонтальная проекция параллельна оси ОХ.

Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без искажений). Поэтому h1, f2, p3 – это натуральная величина соответствующих прямых h, f, p.