Шар
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара.
Граница шара называется шаровой поверхностью, или сферой. Таким образом, точками сферы являются все те точки шара, которые удалены от центра на расстояние, равное радиусу.
Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.
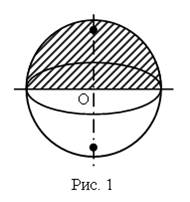
Шар так же, как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси (рис. 1).
Многогранник
Многогранником называется тело, ограниченное конечным числом плоскостей. Граница многогранника называется его поверхностью (рис. 2).
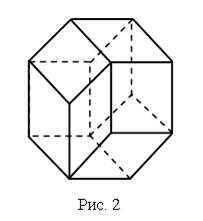
Многогранник называется выпуклым, если он лежит по одну сторону от каждой из ограничивающих плоскостей. Общая часть поверхности выпуклого многогранника и ограничивающей его плоскости называется гранью. Стороны граней многогранника называются ребрами, а вершины – вершинами многогранника.
Поясним данное определение на примере знакомого вам куба (рис. 3). Куб есть выпуклый многогранник. Его поверхность состоит из шести квадратов: ABCD, BEFC, ... . Они являются его гранями. Ребрами куба являются стороны этих квадратов АВ, ВС, BE, ... .
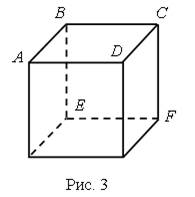
Вершинами куба являются вершины квадратов А, В, С, D, Е, ... . У куба шесть граней, двенадцать ребер и восемь вершин.
Призма
Призмой называется многогранник, образованный заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, которые пересекают плоский многоугольник в одной из плоскостей. Грани призмы, лежащие в этих плоскостях, называются основаниями призмы. Другие грани называются боковыми гранями. Все боковые грани – параллелограммы. Ребра призмы, соединяющие вершины оснований, называются боковыми ребрами. Все боковые ребра призмы параллельны.
Высотой призмы называется расстояние между плоскостями ее оснований. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы. Диагональным сечением призмы называется сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Призма называется прямой, если все боковые грани составляют с основаниями прямые двугранные углы.
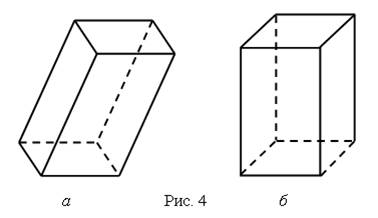
Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани – параллелограммы. На рисунке 4а изображен наклонный параллелепипед, а на рисунке 4б – прямой параллелепипед.
Правильные многогранники
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
Существует пять типов правильных выпуклых многогранников (рис. 5): правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
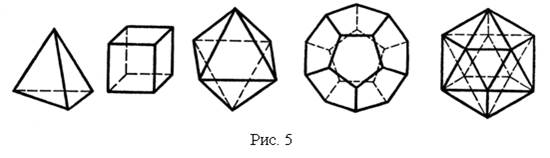
У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
У куба все грани – квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными ребрами.
У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.
У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.
У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.
Урок 4
Двузначные числа и их запись
Цели урока : рассмотреть изображение двузначных чисел с помощью цветных палочек; закреплять навыки сложения и вычитания чисел в пределах 20; совершенствовать навык счёта в пределах 100; развивать логическое мышление и умение анализировать.
Ход урока
I. Организационный момент.
II. Устный счёт.
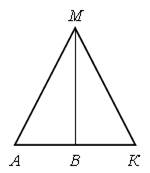
1. Сколько всего отрезков на чертеже?
2. Являются ли эти квадраты «магическими»?
| 3 | 8 | 7 | 7 | 2 | 9 | |
| 10 | 6 | 2 | 8 | 6 | 4 | |
| 5 | 4 | 9 | 3 | 10 | 5 |
3. Решите задачу.
Дети были на экскурсии в музее. На первом этаже они осмотрели 6 витрин, а на втором – на 5 витрин больше. Сколько витрин осмотрели дети на втором этаже?
4. Задание на смекалку.
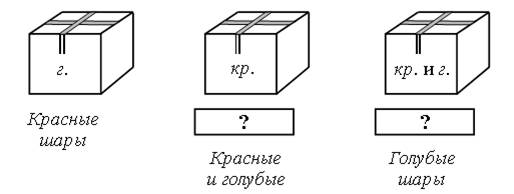
Таня разложила елочные шары в три одинаковые коробки. В одну коробку она положила красные шары, в другую – голубые, а в третью – и те, и другие. Заклеила, и когда стала их надписывать, то перепутала все коробки.
Догадайтесь, какие шары лежат в каждой коробке, если в коробке с надписью «Красные шары» лежат голубые.
III. Сообщение темы урока.
– Сегодня на уроке мы научимся записывать двузначные числа, количество единиц которых не равно нулю.
Дата: 2018-12-28, просмотров: 674.