Начнем с SK оценки

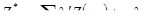
Далее подставим вместо m ее кригинговую оценку m*. Если обозначить вес среднего в простом кригинге l_M,  то

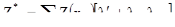                                                           [7.36]

В начале это не похоже на OK оценку. Но так как OK оценка единственна, и если она удовлетворяет уравнению OK, то для нее должно существовать другое выражение. Покажем, что [7.36] удовлетворяет этим уравнениям. Во-первых, мы проверим, что сумма весов равна 1.0. Их сумма дает

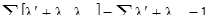                                                           [7.37]

так как 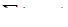. Теперь покажем, что уравнение [7.11]

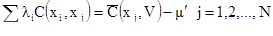                                           [7.38] также удовлетворяется

После замены l_i на l’_i+l_Ml_m первое слагаемое становится:

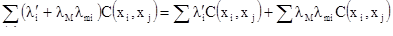   [7.39]

В системе SK первое слагаемое – 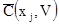. Аналогично в системе кригинга для среднего [7.26] другое слагаемое – . Отсюда

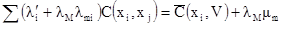                                       [7.40]

Поэтому, установив , становится понятно, что их факторы взвешивания удовлетворяют уравнениям. Поэтому выражение [7.36] удовлетворяет всем уравнениям OK. В заключении, подставив 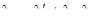 в выражение для дисперсии кригинга, вычисляем новое выражение для дисперсии OK:

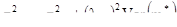                                                                           [7.41]

Наклон линейной регрессии

Во вступительном упражнении в начале книги действительные значения содержаний блоков изображались на одном графике вместе со значениями оценок для различных методов оценивания, включая полигональный метод и кригинг. В идеальном случае 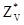 всегда равна 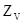, но это невозможно на практике. Очень хорошие результаты получаются, когда оценщик является условно несмещенным; т.е.

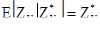                                                                                          [7.42]

Это означает, что регрессия между 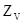 и 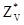 должна быть линейна с наклоном 1.0.

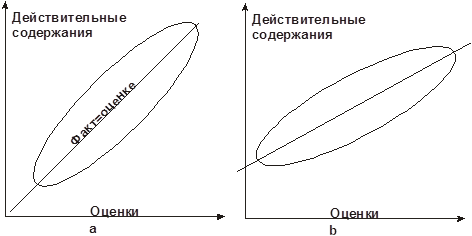
Рис 7.2. Регрессия действительных значений и оценок, (a) условно несмещенная и (b) условно смещенная

Важно отметить, что, хотя кригинг по определению - глобально несмещенный оценщик, так как 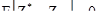, но он не является обязательно условно несмещенным. В этом параграфе мы увидим, что, если предположить линейную регрессию, то простой кригинг будет условно несмещенный, а обычный кригинг нет.

       Далее мы вычислим угол линейной регресси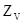и  и 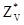 для оценки OK. На практике распределения  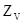и 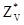 редко известны; поэтому настоящая форма кривой 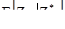, предполагаемой, как функции от 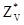, неизвестна. Несмотря на это, наклон линейной регрессии можно использовать, чтобы увидеть, как далеко находится OK оценка от условно несмещенной. Хорошо известно, что наклон, p, линейной регрессии получается из

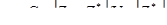                                                                         [7.43]

Для простого кригинга,

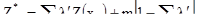                                                                  [7.44]

и поэтому

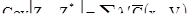
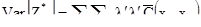                                                                 [7.45]

Из уравнений SK эти два слагаемых равны. Поэтому наклон равен 1.0.[3] Аналогично – для обычного кригинга:

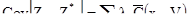
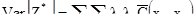
Но т.к.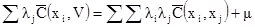

то 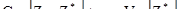,                                                                 [7.47]

и, следовательно, наклон p линейной регресси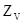и  и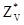

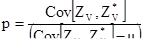                                                                               [7.48]

Здесь значение параметра Лагранжа вычисляется из системы кригинга, записанной в виде ковариаций. Если используется вариограммная форма записи уравнений, то знак меняется на обратный. В общем случае наклон меньше 1.0. Этот результат, касающийся наклона линейной регрессии действительного и оценки, будет использоваться в следующей главе для выбора величины окрестности кригинга.