Сейчас рассмотрим, как оценить дисперсию блоков по вариограмме проб. Обозначим основания с разными объемами, как v (меньшее) и V(большее). Если данные двухмерные, то это будут области, а не объемы. В нашей модели изучаемые переменные предполагаются, как реализации z(x) случайной функции Z(x). Если все значения величины внутри объема V доступны, то можно найти среднее содержание и дисперсию внутри этого объема. Среднее равно

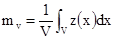                                                                          [6.1]

а дисперсия содержаний внутри объема V

                                                      [6.2]

Здесь 0 означает точку с практически нулевым объемом. Если мы рассмотрим разнообразие реализаций, то дисперсию z(x) внутри V можно получить, как математическое ожидание  для всех возможных реализаций:

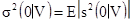                                                                      6.3]

Можно показать, что эта дисперсия связана с вариограммой формулой:

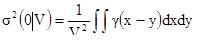                                                      [6.4]

Этот интеграл есть среднее, вычисленное изменением x и y независимо по всему объему V. Поэтому введем обозначение 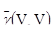. Получим

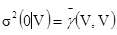                                                                          [6.5]

На практике 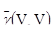 вычисляется дискретизацией блока V. Упражнение 6.1 в конце главы покажет читателю, как производятся такие вычисления.

Дисперсия блоков v внутри блока V

Теперь мы обсудим новую случайную функцию, определенную, как пространственное среднее объема v:

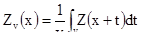                                                                      [6.6]

Цель – найти изменчивость этой новой переменной 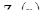 внутри большого объема V. Обычно v представляет собой керновую пробу, а V может представлять горный выемочный блок, или v – суточная добыча, а V – все месторождение.

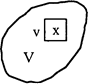
Рис 6.3. Маленький блок v с центром в точке x внутри объема V

Дисперсия v внутри V обозначается 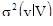 и рассчитывается следующим образом:

                                                            [6.7]

Раскрывая это выражение, получаем:

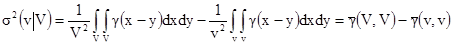    [6.8]

Аддитивное отношение Крига

Объединение результатов [6.5] и [6.8] дает уравнение, называемое аддитивным отношением Крига.

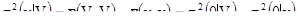                                           [6.9]

Это выражение можно написать для трех объемов v, V и V', где :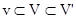

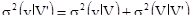                                                                      [6.10]

Например, v может быть секцией керна, V – блоком, а V' - большим участком или всем месторождением. В этом случае формулу можно интерпретировать, как "дисперсия керна внутри месторождения равна дисперсии керна внутри блока плюс дисперсия блока внутри месторождения". Сейчас мы проверим это утверждение для данных, рассмотренных ранее (см. Табл. 6.1). Здесь v соответствует блоку 1м на 1м, а V - блоку 2м на 2м.

Ранее мы получили:

                                                                                                      [6.11]

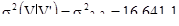                                                                                               [6.12]

Значение  можно вычислить, как дисперсию четырех малых блоков внутри одного большого. Получаем 10,951. Легко проверить, что это значение эквивалентно 27,592-16,641 и, следовательно, удовлетворяет аддитивному отношению. На самом деле это справедливо для всех случаев, где малые блоки v полностью заполняют больший по размеру блок, здесь – V.