Обозначим за Z(x) случайную функцию, определенную на точечном основании. Ее среднее для объемов V определяет новую случайную функцию Zv (x) с основанием V. Можно показать, что вариограмма этой новой регуляризованной переменной:
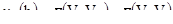[6.15]
где Vh обозначает основание V, перемещенное на расстояние h (преобразованное вектором h), а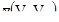 
представляет собой среднее значение вариограммы между произвольной точкой в Vh и другой точкой в V.
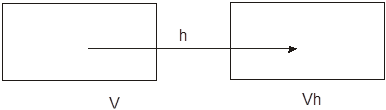
Рис 6.4. Объем V, перемещенный вектором h в объем Vh
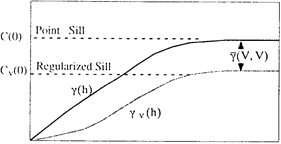
Когда расстояние h мало по сравнению с размером V, то расстояние от произвольной точки в V до произвольной точки в Vh может значительно меняться. Например, если V – прямоугольник с длиной l, то горизонтальные расстояния меняются от H-l до h+l. Однако, когда длина h значительно больше размера V, то все расстояния довольно близки к h. Следовательно, среднее значение вариограммы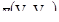 
приблизительно равно g(h). Поэтому мы определим зависимость:
{6.16]
Рис 6.5. Вариограмма с точечным основанием и регуляризованная вариограмма
Упражнение: вычисление регуляризованных вариограмм
Данные, используемые для оценки запасов, не всегда имеют одинаковый размер основания. Например, одни скважины могут иметь диаметр 8 дюймов, а другие - 2 дюйма. Важно иметь возможность вычислить вариограммы, соответствующие этим двум основаниям. Мы рассчитаем модели вариограмм для блоков 2м на 2м и 3м на 3м и получим, что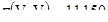 
для блоков 2м на 2м и 
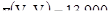для блоков 3м на 3м.
Решение
Для блоков 2м на 2м
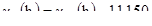[6.17]
Для блоков 3м на 3м
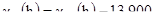[6.18]
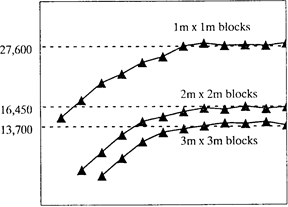
В результате теоретические пороги регуляризованных вариограмм равны 16,450 и 13,700 соответственно. На Рис. 6.6 изображены эти три экспериментальные вариограммы. Их пороги близки к вычисленным теоретически.
Рис 6.6. Экспериментальные вариограммы для трех размеров оснований
Упражнения
Чтобы выполнить эти упражнения, сначала нужно вычислить значения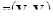 
. Для этого существует два пути: написание небольшой вычислительной программы для дискретизации V или использование стандартных таблиц и номограмм, таких которые приведены в работе Journel и Huijbregts (1978) на стр. 125-147. Первый пример использует компьютерное вычисление, а второй показывает, как пользоваться таблицами.
Упр 6.1 Вычисление 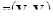с помощью дискретизации блока. Это упражнение предполагает вычисление среднего значения вариограммы через дискретизацию блока V.Во-первых, нужно выбрать количество ячеек сетки для каждой оси, потому что оно определяет координаты точек дискретизации.
Процедура состоит из цикла, который берет каждую пару точек, вычисляет вектор расстояния между ними, оценивает соответствующее значение вариограммы и складывает полученные значения. В заключении сумма делится на квадрат количества ячеек сетки дискретизации для получения среднего значения вариограммы.
Выбор количества ячеек сетки очень важен. Если ячеек слишком мало, то среднее будет неточным; если наоборот, то время вычислений будет слишком велико. Например, если квадрат разделить на 100 на 100 точек; получаем 104 точек и 108 слагаемых вариограммы. Обычно достаточно от 25 до 100 точек в двухмерном пространстве и 200-300 точек в трехмерном пространстве.
Напишите компьютерную программу для вычисления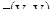 
и 
, где V – блок 100м на 100м и v – блок 10м на 10м и где вариограмма:
сферическая с зоной 100м и порогом 3.0,
экспоненциальная с практической зоной 50м и порогом 3.0,
чистый эффект самородка с порогом 3.0.
Начните вычисления, используя дискретизацию 2 на 2, и продолжите их до значения 10 на 10, обращая внимание на стабилизацию величины 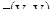и увеличение времени вычислений.
Упр 6.2 Вычисление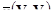 
с помощью таблиц. Это упражнение иллюстрирует использование стандартных таблиц, которые можно найти в текстах опубликованных работ, например Journel и Huijbregts (1978). Главы 4 и 5 (стр 128-9) приводят стандартные значения 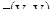для сферической вариограммы с единичной зоной и единичным порогом для двухмерных и трехмерных блоков соответственно. Ключом к использованию этих таблиц является преобразование размера блока в долю зоны (или масштабного коэффициента "а" для экспоненциальной вариограммы) и, затем прочтение требуемых значений из таблицы.
Например, если блок имеет размер 100м на 100м, вариограмма сферическая с зоной 200м и порогом 3.0, то блок эквивалентен размеру 0.5 на 0.5 зоны. Таблица дает значение 0.375. Подставляя порог, получаем
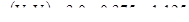
Используем таблицы для вычисления 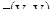и 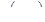, где V – блок 100м на 100м и v - блок 10м на 10м, где вариограмма :
сферическая с зоной 100м и порогом 3.0,
экспоненциальная с практической зоной 50м и порогом 3.0,
эффект самородка с порогом 3.0 (зона = 0).
Сравните ваши результаты с итогами, полученными в предыдущем упражнении.
Упр 6.3 Вычисление 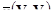теоретически. В некоторых простых случаях 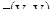можно вычислить через интеграцию, используя уравнение [6.4]. Пусть V будет секцией керна длиной d (одномерный случай).
Если вариограмма линейна с наклоном C, то покажите, что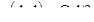 
. Помните, что 
.
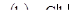Вычислите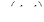 
для случая, когда вариограмма экспоненциальная с порогом C и практической зоной 3.
Вычислите 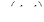для случая, где вариограмма является эффектом самородка с порогом C.
Упр 6.4 Дисперсия изменчивости. Используйте значения 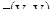и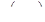 
, найденные выше, для вычисления дисперсии изменчивости блоков 10м на 10м внутри области размером 100м на 100м для случаев, где вариограмма :
сферическая с зоной 100м и порогом 3.0,
экспоненциальная с практической зоной 50м и порогом 3.0,
эффект самородка с порогом 3.0 (зона = 0).
Упр 6.5 Дисперсия изменчивости. Небольшая добывающая компания добывает в карьере каждый день 4 блока размером 10м на 10м на 5м. Менеджер по добычи может выбрать вариант добычи 4-х смежных блоков (т.е. 40м на 10м на 5м) или блоков из разных частей карьера, которые расположены на большом расстоянии друг от друга, чтобы считать их некоррелированными. Задание заключается в прогнозе ежедневного разброса среднего содержания для обоих вариантов. Добываемая руда имеет сферическую вариограмму с зоной 100м и порогом 3.0.
Упр 6.6 Регуляризованные вариограммы. Содержание меди в секциях керна длиной 5м имеет сферическую вариограмму с вертикальной зоной 50м, порогом 1.0 и эффектом самородка 0.05. Если высота уступа во время добычи будет равна 15м, то данные будут композированы по этой высоте. Мы хотим вычислить вертикальную вариограмму для этой новой композированной переменной. Во-первых, вычислите 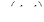, где d –секция керна длиной 15м, затем рассчитайте и постройте вариограммы для секций 5м и 15м на одном графике.
Теория кригинга
Содержание
Эта глава представляет теорию кригинга. Кригинг – это метод оценивания, который дает наилучшую несмещенную линейную оценку значений точек или средних содержаний блоков. Здесь "наилучшая" означает минимальную дисперсию. Обсуждается три типа кригинга: обыкновенный кригинг (ordinary kriging, OK), используемый, когда среднее содержание неизвестно, кригинг неизвестного среднего и простой кригинг (simple kriging, SK), используемый, когда среднее содержание известно.
Уравнения этих трех оценок выведены для стационарного случая и обобщаются для случая внутренних переменных для ОК. Доказывается теорема аддитивности, которая позволяет установить связь между OK и SK. Для обыкновенного кригинга дается формула наклона графика линейной регрессии действительных значений и их оценок, а также обсуждается ее важность в связи с условной несмещенностью. В заключении кригинг представляется, как точный интерполятор.
Цель кригинга
Опробование обеспечивает точную информацию в точках взятия проб. Однако оно не информирует нас, что происходит между этими точками. Поэтому нам нужен точный способ оценивания значений в промежуточных точках или средних по блокам. Точность оценивания зависит от нескольких факторов:
· количество проб и качество данных в каждой точке.
· расположение проб по месторождению. Равномерно расположенные пробы дают больше информации о месторождении, чем неравномерно сгруппированные данные.
· расстояние между пробами и точкой или оцениваемым блоком. Действительно, чем дальше расположена проба, тем труднее ей доверять. Поэтому мы ожидаем, что точность выше для близких проб, и уменьшается с увеличением расстояния. Здесь не нужно объяснять опасность экстраполяции за пределы зоны опробования.
· пространственная непрерывность рассматриваемой переменной. Легче оценить величину регулярной переменной, чем той, которая меняется произвольно. Например, для данного расположения проб, оценки содержания меди более точны, чем оценки золота.
"Кригинг" – метод оценивания, который учитывает все эти факторы. Он назван в честь доктора Д. Г. Крига (Dr D.G. Krige), южноафриканского горного инженера, который первым разработал метод движущего среднего для оценки содержания золота, чтобы убрать эффект регрессии. Профессор Дж. Матерон (Prof. G. Matheron) улучшил эту методику, и новый метод был назван кригингом. По существу, это способ нахождения лучшей несмещенной линейной оценки (в смысле наименьшей дисперсии). Это значит, что мы выбираем взвешенное среднее величин проб, которые имеют минимальную дисперсию.
Дата: 2018-12-28, просмотров: 387.
