Как уже упоминалось во введении, расчет режимов трехфазных цепей основывается на тех же приемах и методах, что и расчет любой электрической цепи синусоидального тока. Поэтому предполагается, что, справившись со второй задачей, студент готов рассчитать и цепь, в которой действуют три одинаковые по величине ЭДС, начальные фазы которых сдвинуты между собой на 120°. Для демонстрации учета этой особенности приводится пример расчета режима для наиболее сложного пункта задания: расчет режима трехфазной цепи с несимметричной нагрузкой, соединенной звездой без нейтрального провода.

Пример. В трехфазную сеть с линейным напряжением U _л=380 В включен звездой приемник. Известно, что в фазе А активное R=22 Ом, в фазе В отрицательное реактивное, т. е. емкостное сопротивление Х=-22 Ом и в фазе С положительное, т.е. индуктивное Х=22 Ом. Выбор индуктивного или емкостного сопротивления определяется исходя из формулы реактивного сопротивления последовательного соединения Х=Х_L - Х_С. Таким образом, простейшая эквивалентная схема замещения для ветви может содержать либо одну емкость при отрицательном реактивном сопротивлении (если положим Х_L=0) или одну индуктивность при положительном реактивном сопротивлении ветви (если положим Х_С = 0).

В результате схема заданной цепи должна выглядеть так (рис. 3.2):

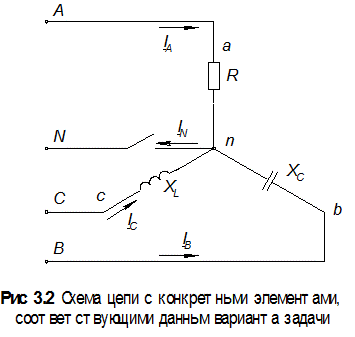
Решение. Расчет производится комплексным методом. Находим значения фазных напряжений:

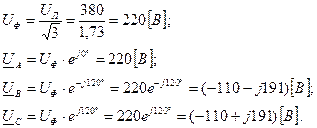
Определяем значения напряжения между нейтральными точками приемника и источника питания:

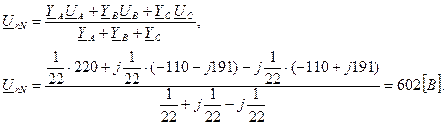
Определяем значения напряжений на зажимах фаз приемника:

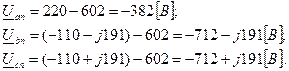
Определяем значения фазных (линейных) токов:

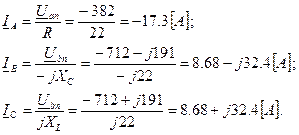
Векторная диаграмма токов с топографической диаграммой потенциалов изображена на рис. 3.3(при построении диаграммы комплексную плоскость поворачивают на 90° против часовой стрелки). Из рассмотрения этой задачи следует, что значения напряжений на зажимах фаз приемника получаются неодинаковыми. Поэтому несимметричные приемники (бытовые и др.) соединяют либо четырехпроводной звездой, либо треугольником.

На приведенной топографической диаграмме точка «n» попала на ось действительных. Однако она может быть и далеко в стороне от нее в задачах других вариантов. Ведь не везде модули комплексных сопротивлений всех фаз одинаковы.

Надо заметить, что это не единственный метод решения задачи. Студент может воспользоваться любым другим, известным ему методом, например, методом контурных токов. В самом деле, представив напряжения источника в виде ЭДС фаз генератора или трансформатора, можно рассматривать цепь как достаточно простую двухконтурную.

Как видим, для решения задачи предстоит составить и решить систему двух уравнений относительно контурных токов I₁₁ и I₂₂ , после чего находим значения силы токов в ветвях I _А = I ₁₁ , I _В = I ₂₂ , I _С = - ( I ₁₁ + I ₂₂ ).

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Борисов, Ю. М. Электротехника. Учебник для вузов - 2-е изд., перераб. и доп. /Ю. М. Борисов и др. - М.: Энергоатомиздат, 1985 (и все последующие издания).

Касаткин, А. С. Электротехника. Учебное пособие для вузов. - 4-е изд. /

А. С. Касаткин, М. В. Немцов: - М.: Энергоатомиздат, 1983 (и последующие издания).

Бессонов, Л. А. Теоретические основы электротехники /Л. А. Бессонов. - М.: Высшая школа, 1973 (и все последующие издания).

Нейман, Л. Р. Теоретические основы электротехники т.1/Л. Р. Нейман, К. С. Демирчян. - М. - Л.: Энергия, 1965 (и все последующие издания).

СОДЕРЖАНИЕ

ВВЕДЕНИЕ…………………………………………………………

Задача 1. Расчет цепи постоянного тока……………………………

Задача 2. Расчет цепи синусоидального тока………………………

Задача 3. Расчет трехфазной цепи…………………………………

БИБЛИОГРАФИЧЕСКИЙ СПИСОК……………………………….