Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Использование комплексных токов, сопротивлений, напряжений и ЭДС при расчете цепей синусоидального тока символическим методом позволяет использовать все методы, известные нам, для расчета цепей постоянного тока. Только вместо алгебраических уравнений с действительными коэффициентами придется составлять и решать уравнения с комплексными коэффициентами. Это касается и законов Кирхгофа, и метода узловых напряжений и т. д.

Пример. Рассчитать электрическую цепь синусоидального тока со смешанным соединением приемников.

 

 

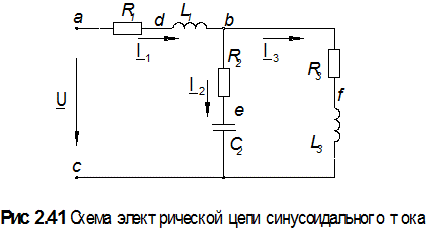
Для схемы, изображенной на рис. 2.41, известно, что:

U = 120 B, R₁ = 10 Ом,              R ₂ = 24 Ом,     R ₃ = 15 Ом,

L ₁ = 19,1 мГн,              L ₃ = 63,5 мГн, C ₂ = 455 мкФ, f = 50 Гц.

Определить значения силы токов I ₁ , I ₂ , I ₃ в ветвях цепи, составить баланс мощностей и построить векторную диаграмму токов, совмещенную с топографической диаграммой потенциалов.

 

Решение методом преобразования

Рассмотрим это на примере расчета токов в электрической цепи синусоидального тока методом, известным нам со школьного курса физики, методом преобразования, когда параллельное соединение сопротивлений заменяется их общим сопротивлением, последовательное соединение тоже одним эквивалентным ему сопротивлением, и таким образом схему упрощают, пока не получат нагрузку источника в виде одного единственного сопротивления. Дальше решение сводится в основном к использованию закона Ома.

Выражаем сопротивления ветвей цепи в комплексной форме:

 

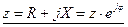
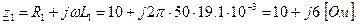
Переходя от алгебраической формы записи комплексного числа к показательной, получаем:

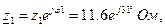
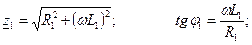где

 

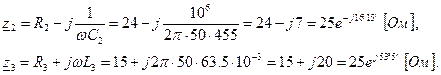Выражаем заданное напряжение в комплексной форме. Если начальная фаза напряжения не задана, то ее можно принять равной нулю и считать вектор напряжения совпадающим по направлению с положительным направлением действительной оси на комплексной плоскости. В этом случае мнимая составляющая комплексного числа, выражающего значение напряжения, будет отсутствовать (рис. 2.42): U = U = 120 B .

Значение полного комплексного сопротивления цепи:

 

 

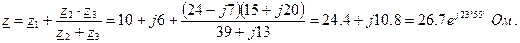Определяем значение силы тока I ₁ в неразветвленной части цепи:

 

 

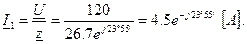Токи в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:

 

 

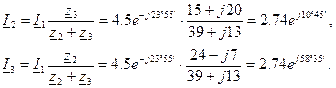Значения силы токов I ₂ и I ₃ можно найти и по-другому:

 

 

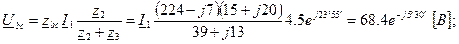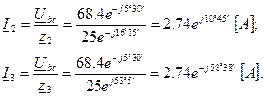Метод контурных токов

Для сравнения приведем решение этой же задачи методом контурных токов.

Подготовим схему к составлению уравнений по методу контурных токов. Для этого на схеме (рис. 2.52) надо показать направления обхода контуров и обозначить сами контурные токи.

 

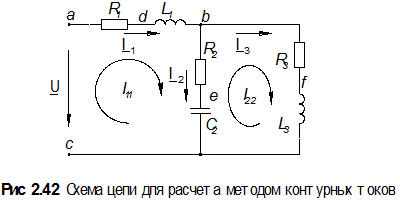Теперь, как и в предыдущей задаче, составляем уравнения, в которые в качестве неизвестных входят контурные токи, а в качестве коэффициентов при них собственные и смежные сопротивления контуров. Разница в том, что и токи, и коэффициенты будут комплексные:

 

 

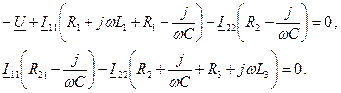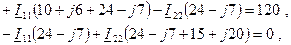Значения активных сопротивлений нам даны в условии задачи, а реактивные сопротивления вычислены при расчетах методом преобразования. Воспользуемся ими и получим уравнения с численными комплексными коэффициентами. Заодно перенесем свободный член - U в правую часть, изменив его знак:

 

 

или

 

 

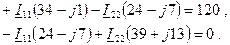Главный определитель системы

 

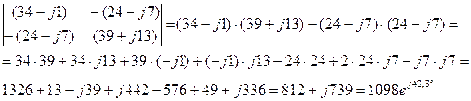
При этих расчетах студенты очень часто забывают, что j · j = j ² =-1, и то, что большинство калькуляторов, для вычисления арктангенса используют только результат деления, выдают ответ для первой четверти при положительном результате деления, тогда как при отрицательных значениях одновременно и числителя, и знаменателя значение угла должно лежать в третьей четверти тригонометрического круга. Если же результат деления отрицательный, то калькулятор выдает ответ для угла в четвертой четверти, хотя при отрицательном знаменателе и положительном числителе правильное значение угла находится во второй четверти. За этим приходится следить самому расчетчику и иногда делать дополнительные поправки. Заметим так же, что показатель степени в последнем выражении записан в градусах, хотя с математической точки зрения это не корректно. Формулы преобразования алгебраической формы комплексного числа в показательную предполагают запись аргумента (показателя степени е) в радианах. В литературе же по использованию комплексного метода в электротехнических расчетах такая «вольность» допускается и привилась достаточно широко.

Найдем значения первого и второго определителей, заменив сначала первый столбец в главном определителе на столбец свободных членов, для нахождения второго определителя второй столбец:

 

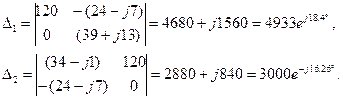
Найдем значения контурных токов и токов в ветвях:

 

 

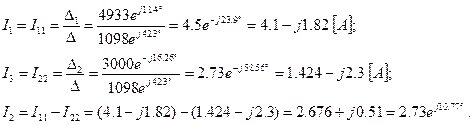
Как видим, отличия очень небольшие, да и те, по-видимому, за счет округлений во время вычислений.

Проверка баланса мощности

Полная комплексная мощность всей цепи равна:

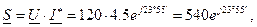
где 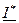– число комплексно-сопряженное комплексу действующего значения тока I ₁ , потребляемого от источника.

Для получения I ^* - надо изменить знак перед мнимой частью I ₁ в алгебраической форме или перед показателем степени е в показательной (экспоненциальной) форме.

Для определения значений активной и реактивной мощностей представим полную комплексную мощность в алгебраической форме. Тогда действительная часть комплекса будет представлять собой активную мощность, а коэффициент при мнимой - реактивную.

 

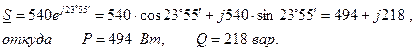
Иная запись этого же действия выглядит так:

 

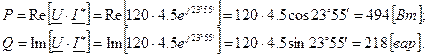
В этом случае Re означает реальную часть комплексного числа (произведения UI^*), а Im - мнимую часть.

Отметим, что значение полной мощности измеряется в вольт-амперах (В·А), а реактивная - в вольт-амперах реактивных (вар).

Значения активной и реактивной мощности можно найти и по-другому, как мощности, потребляемые отдельными потребителями цепи:

 

P₁ = R₁I₁² = 10-4,5² = 202 Вт; P₂ = R₂I₂² = 180 Вт; P₃ = R₃I₃² = 112 Вт;

Q₁ = X1 I₁² = 6·4,52 = 122 вар; Q₂ = X₂ I₂²= -52,5 вар; Q₃=X₃ I₃² =150 вар.

Проверка показывает, что P = P ₁ +P₂+P₃ , что Q ≈ Q ₁ + Q ₂ + Q ₃ .

Эти равенства значений для активной и реактивной мощностей называются балансом мощности и, в частности, могут служить проверкой правильности решения задачи. Суть в том, что в силу закона сохранения энергии суммы активных и реактивных мощностей, выданных источниками, должна быть равна суммам значений активных и реактивных мощностей, израсходованных потребителями.

 

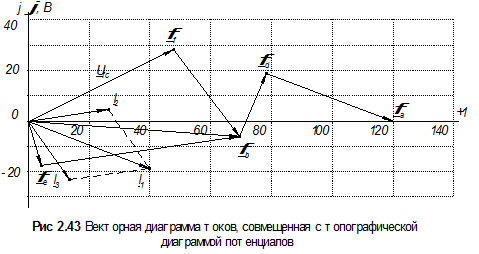
На рисунке (рис. 2.43) приведена векторная диаграмма токов, совмещенная с топографической диаграммой потенциалов цепи. Порядок ее построения следующий.

Строим оси комплексной плоскости: ось действительных (как правило, горизонтальная ось) и ось мнимых (как правило, вертикальная ось). Выбрав удобный масштаб для тока, из начала координат проводим векторы I ₁ , I ₂ и I ₃. Можно воспользоваться алгебраической формой записи, откладывая по осям действительные и мнимые части комплексных изображений этих токов, можно использовать показательную форму, тогда вектор, изображающий соответствующий ток 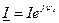, откладывается из начала координат под углом ψ _i к оси действительных (против часовой стрелки, если ψ _i> 0, и по часовой, если ψ _i<0). Это и будет векторной диаграммой токов. Конечно, при правильном решении должен выполняться 1-й закон Кирхгофа в векторной и в комплексной формах: I ₁ = I ₂ + I ₃ или I ₁ + I ₂ = I ₃.

Топографическая диаграмма напряжений показывает на комплексной плоскости значения комплексных потенциалов всех точек цепи, разделенных какими-либо элементами. Отрезки, соединяющие точки на этой диаграмме, представляют собой векторные изображения на комплексной плоскости напряжений между соответствующими точками цепи. Надо только помнить, что в отличие от стрелок, изображающих напряжение на схеме цепи, векторы напряжений на топографической диаграмме направлены в сторону потенциала, обозначенного первым индексом напряжения. Так, вектор U_ab направлен от точки φ _b к точке φ _a.

Расчет самих комплексных потенциалов ведется почти так, как мы это делали для потенциальной диаграммы в задаче 1. Так, приняв потенциал нижней клеммы источника (или, что тоже, точки С) равным нулю, поместим его в начало координат комплексной плоскости. U _bc =φ _b -φ _c =φ _b . Из последнего ясно, что найденное нами ранее значение U _bc как раз и есть потенциал точки «b» и может быть показан на комплексной плоскости в точке, на которую укажет вектор длиной, соответствующей 68,4В, проведенной под углом -5°30' к оси действительных. Путь тока между точками «b» и «c» может лежать через две ветви, в каждой из которых есть своя точка, потенциал которой отличен как от φ _b, так и от φ _c. Это точки «e» и «f». Их потенциалы можно определить как

 

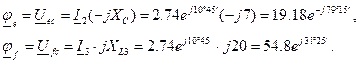
При вычислениях надо помнить, что j = e^{j 90°}, а - j = e ^-j90°. Остается определить положение потенциалов точек «d» и «a». Имеем:

 

 

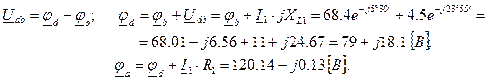
Как видим, мы пришли в точку, лежащую почти на оси действительных на расстоянии, соответствующем 120 В от начала координат (от точки φ). Сюда мы и должны были прийти, если учесть, что напряжение между точками «a» и «c» по условию равно 120 В, а начальную фазу этого входного напряжения мы приняли равной нулю.

 

ЗАДАЧА 3. РАСЧЕТ ТРЁХФАЗНОЙ ЦЕПИ.

 

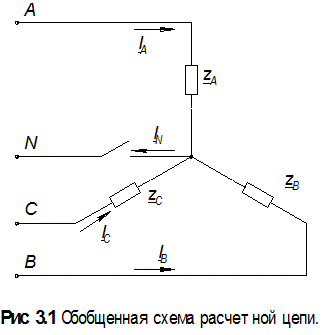1. Выбрать из таблицы 3.1 величины активных и реактивных сопротивлений фаз для цепи, заданной схемой (рис. 3.1).

2. Нарисовать простейшую схему трехфазной цепи с условным изображением активных сопротивлений, индуктивностей и емкостей, соответствующих данным задачи.

3. Рассчитать значения всех токов в цепи с подключенным нейтральным проводом.

4. Рассчитать значения всех токов в цепи при отключении нейтрального провода.

5. Рассчитать значения всех токов при обрыве фазы, указанной, в таблице 3.1 с подключенным нейтральным проводом.

6. Рассчитать значения всех токов при обрыве фазы с отключенным нейтральным проводом.

7. Рассчитать значения всех токов в цепи при коротком замыкании фазы и отключенном нейтральном проводе.

8.  Построить векторную диаграмму

9. Подсчитать активную мощность, потребляемую цепью, для рассчитанных режимов.

 

Таблица 3.1

Вари-анты	Uл В	RА Ом	ХА Ом	RB Ом	ХВ Ом	RC Ом	ХС Ом	Обрыв фазы	КЗ фазы
1	2	3	4	5	6	7	8	9	10
1	127	30	30	30	-	30	-	С	В
2	127	30	-20	40	-	40	-	С	В
3	127	40	30	50	-	-	50	С	В
4	127	20	-40	30	-	-	30	С	В
5	127	40	40	40	-	-	-50	С	В
6	220	20	-20	30	-	-	-30	С	В
7	220	15	15	-	15	15	-	В	С
8	220	20	-15	-	30	30	-	В	С
9	220	20	20	-	-30	30	-	В	С
10	220	30	-30	-	-40	40	-	В	С
11	380	20	20	-	40	-	40	В	С
12	380	20	-30	-	30	-	40	В	С
13	380	40	40	-	-50	-	50	В	С
14	380	40	-40	-	-50	-	50	В	С
15	380	30	40	-	40	-	-40	В	С
16	127	8	-10	-	15	-	-50	В	С
17	127	15	15	-	-20	-	-20	В	С
18	127	15	-20	-	-15	-	-20	В	С
19	127	20	-	30	15	30	-	С	А
20	127	25	-	20	-15	25	-	С	А
21	220	15	-	10	10	-	15	С	А
22	220	20	-	20	-15	-	25	А	С
23	220	50	-	30	40	-	-50	А	С
24	220	50	-	30	-40	-	12	А	С
25	220	-	-20	-	20	16	-	А	В
26	380	-	20	16	12	20	-	А	С
27	380	-	-30	24	18	30	-	А	С
28	380	-	25	20	-15	25	-	А	С
29	380	-	50	40	30	50	-	А	С
30	380	-	40	32	24	-	40	С	А
31	127	-	10	-	-10	8	-6	В	А
32	127	-	-15	-	-15	12	9	В	А
33	127	-	-20	-	-20	12	-16	В	А
34	127	-	30	-	-30	24	-18	В	А
35	127	-	45	-	-45	27	36	В	А
36	220	-	45	27	36	-	-45	В	С
37	220	-	-50	40	-30	-	-50	А	С
38	220	-	-30	-	30	24	-18	А	В
39	220	-	35	-	35	21	-28	В	А
40	220	-	25	-	25	16	20	В	А