 |
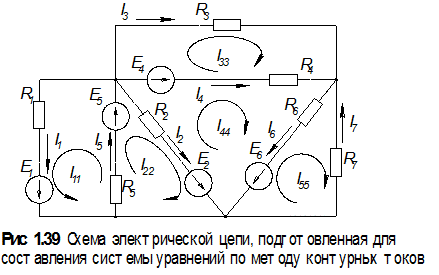
Воспользуемся уже имеющимися стрелками в схеме (рис. 1.38) для обозначения условных положительных направлений токов в ветвях и обходов контуров. Будем считать, что в каждом из контуров в направлении обхода течет свой контурный ток: I11 в контуре 1; I22 в контуре 2 и т. д.
Система уравнений относительно контурных токов выглядит так:
| R11·I11 | +R12·I12 | =E11 | |||
| R11·I11 | +R22·I22 | +R24·I44 | =E22 | ||
| R33·I33 | +R34·I44 | =E33 | |||
| R42·I22 | +R43·I33 | +R44·I44 | +R45·I55 | =E44 | |
| R54·I44 | +R55·I55 | =E55 |
где собственные сопротивления контуров равны
R11=R1+R5, R22=R2+R5, R33=R3+R4, R44=R2+R4+R6, R55=R6+R7.
Общие сопротивления смежных контуров равны
R12=R21=R5; R24=R42=-R2; R34=R43= -R4; R45=R54= -R6.
Контуры 1-й и 3-й; 1-й и 4-й; 1-й и 5-й, а также 2-й и 3-й; 2-й и 5-й; 3-й и 5-й не имеют общих сопротивлений, поэтому не являются смежными, и в уравнениях пустуют места, предназначенные для членов с соответствующими общими сопротивлениями.
Сразу заметим, что при одинаковом выборе направлений контурных токов (все по часовой стрелке или все против часовой стрелки) вероятность сделать ошибку в знаке общих сопротивлений смежных контуров уменьшается.
Контурные ЭДС равны:
E11= E1+ E5; E22= E2+ E5; E33= - E4; E44= - E2+ E4+ E6; E55= - E6.
Как видим, система уравнений оказалась менее громоздкой, однако ее решение дает значение пока только контурных токов. После этого предстоит дополнительная работа по отысканию значений токов в ветвях. Так, I 1 состоит только из контурного тока I 11 ; I 5 – из I 11 и I 22, т. е. I5= I11+ I22, а значение силы тока I 4 представляет алгебраическую сумму значений силы токов I 44 и I 33 : I 4 = I 44 - I 33 и т. д. (следите за знаками).
Решение задачи методом узловых напряжений
Оставив ранее принятые условные положительные направления токов в ветвях, обозначим цифрами узлы цепи, отличающиеся потенциалами.
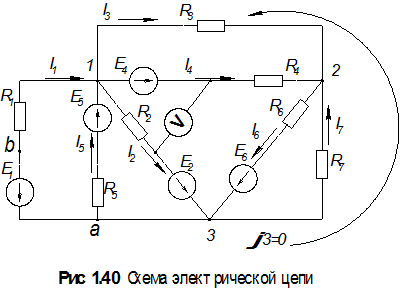 |
Точка «a» имеет, очевидно, потенциал узла 3 и не выделяется нами в особый узел, потенциал которого надо искать, хотя к ней подходит более двух проводников. Точка «b» имеет отличный от них потенциал, но не является узлом. Потенциал одного из узлов принимаем равным нулю.
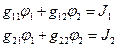 |
В нашем случае выбор (произвольно) пал на узел 3, составим систему уравнений
проводимости, входящие в уравнения, равны:
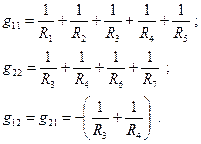 |
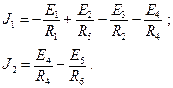 |
Узловые токи равны:
Как видим, слагаемые, содержащие ЭДС, направленные от соответствующего узла, входят в сумму со знаком «минус», к узлу - со знаком «плюс».
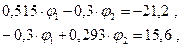 |
Система уравнений в числовой форме имеет вид:
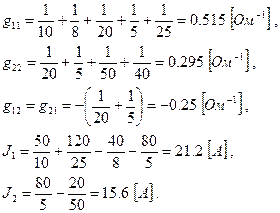 |
где
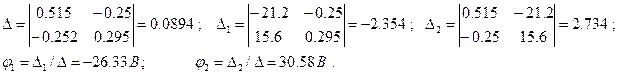 |
Решение системы методом определителей дает значение потенциала узлов 1 и 2:
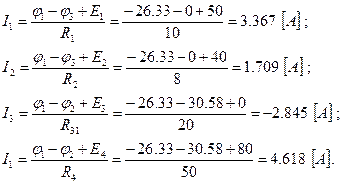 |
Значения силы токов в ветвях найдем по закону Ома с учетом того, что φ3=0:
Остальные значения силы токов определяются аналогично. Результаты представлены в следующей таблице.
Таблица 1.3
| I1, A | I2, A | I3,A | I4, A | I5, A | I6, A | I7, A | Метод |
| 2,367 | 1,709 | -2,845 | 4,618 | 5,853 | 1,011 | -0,763 | Узловых напряжений |
| 2,368 | 1,709 | -2,845 | 4,621 | 5,853 | 1,012 | -0,764 | Контурных токов |
| 2,368 | 1,709 | -2,845 | 4,621 | 5,853 | 1,011 | -0,764 | Законов Кирхгофа |
Дата: 2018-12-28, просмотров: 853.