Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Пример 1

В этом примере вычисления выполнены с использованием широко распространенной программы MathCAD. Соответствующие записи перенесены в текст документа в основном без преобразований и выглядят так же, как в MathCAD. Будем надеется, что студент без труда сопоставит запись E1:=30 с известным ему из программирования выражением «Е1 присвоить значение 30». Кроме того, студенту известно, что в языках программирования довольно часто индексы проставляются «в рост» с основным обозначением величины, так что Е1 в обычном тексте соответствует записи Е₁.

Схема электрической цепи и числовые данные представлены ниже:

Значения ЭДС даны в вольтах, а сопротивлений в Омах.

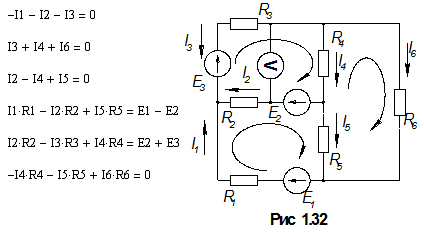Перед составлением уравнения, выберем условные положительные направления токов и положительные направления обходов контуров. Составим уравнения по законам Кирхгофа.

 

При составлении следим за направлениями токов и ЭДС, и в случае их несовпадения с направлениями обхода контуров приписываем напряжениям, созданным этими токами, знак минус. При составлении уравнений по первому закону Кирхгофа входящие в узел токи (по нашим произвольно направленным стрелкам) считаем положительными, а выходящие из узла пишем со знаком минус. Впрочем, если припишем им противоположные знаки, правильность составления уравнений не нарушится, как не нарушается правильность уравнения при умножении левой и правой частей на минус единицу.

Соответствующие этой системе матрицы коэффициентов и свободных членов выглядят так:

Проводим обычные операции для нахождения корней уравнений:

 

Получаем ответ:

 

Вектор значений токов читается элементами сверху вниз I₁, I₂, I₃, I₄, I₅, I₆, т. е. эту запись надо читать так: I₁ = 1,289 А, I₂ = -0,317 А и т. д.

Систему из шести уравнений с шестью неизвестными решать вручную очень громоздко, поэтому лучше найти возможность использовать ЭВМ. Инструмент MATHCAD, например, имеет в составе своих средств вычислений решение систем алгебраических уравнений несколькими методами.

Один из матричных методов приведен выше, другой метод последовательных приближений используем далее. В последнем случае надо только задать (произвольно) нулевое приближение значений неизвестных токов (в процессе решения системы машиной они будут уточняться до заданной точности) и записать систему уравнений в привычном виде. Перед системой обязательно ключевое слово MATHCAD: «Given»

 

Затем указываем, как мы решили обозначить неизвестные (или массив неизвестных если их несколько) с ключевым словом «find» – «найти» и перечисляем в скобках имена неизвестных. Вектор неизвестных мы обозначили Strom (по-немецки ток)

И, наконец, «велим» MATHCAD вывести найденные значения на экран (Пишем: Strom =). После чего на экране появляется вектор вычисленных значений:

Здесь сверху вниз по порядку идут значения вычисленных токов: I1, I2 и т. д.

 

Метод контурных токов

Будем считать (в теории доказано, что этот прием приводит к верным результатам), что в каждом контуре течет свой контурный ток. Пусть они совпадают по направлению с уже выбранными направлениями обходов контуров. Чтобы отличить их в обозначениях от токов в ветвях, будет отмечать их двойной индексацией: I_kk, где индекс kk показывает номер (k -й) рассматриваемого контура. Представим, что токи в ветвях состоят из контурных токов. Так, во внешних ветвях протекают (при выбранных нами конурах) только по одному контурному току: через сопротивление R ₃ контурный ток I ₁₁, навстречу току I ₃. Так что, по-видимому, I ₃ = – I ₁₁ , аналогично I ₁ = I ₂₂ и I ₆ = I ₃₃.

Последние пары токов (контурных токов и токов в ветвях) совпадают по направлению, и потому знаки минус отсутствуют.

По сопротивлениям R ₂, R ₄, R ₅ протекают по два контурных тока в противоположных направлениях. Их разности (или алгебраические суммы) и составляют истинные значения силы токов в ветвях.

При составлении алгебраических сумм положительным считается контурный ток, совпадающий по направлению с выбранным изначально положительным направлением тока в ветви. Имеем:

I ₂ = I ₁₁- I ₂₂ , I ₄ = I ₁₁- I ₃₃ и I ₅= I ₂₂ – I ₃₃ .

Таким образом, достаточно нам знать всего три контурных тока для нахождения значения силы токов в ветвях. Значит, если мы сумеем правильно составить систему уравнений относительно контурных токов, то придется решать систему трех уравнений вместо шести. Такую систему уже несложно решать вручную.

Введем понятие собственного сопротивления контура, представляющее сумму всех сопротивлений данного контура (в тексте показаны знаки присваивания, как это записывается в MATHCAD и часто на языках программирования высокого уровня:

Введем также понятие смежного сопротивления контуров, это сопротивление, входящее одновременно в два контура. Смежные сопротивления имеют разные индексы:

Знаки «-» в правой части обусловлены тем, что контурные токи смежных контуров протекают по сопротивлениям R 2, R 4 и R 5 в противоположные стороны. Если бы мы решили направить обход третьего контура и сам ток I₃₃ против часовой стрелки, то писали бы:

R 12 : = - R 2, R 23 : = R 4, R 13 : = R 5.

Отметим, что всегда:

R 21= R 12 R 32= R 23 R 31 = R 13

Введем понятия контурных ЭДС, представляющие алгебраические суммы всех ЭДС соответствующего контура:

 

Для решения на MATHCAD зададим любые начальные значения контурных токов (например, все по одному амперу):

 

Составим систему уравнений по методу контурных токов и решим ее.

 

Если бы мы не вводили понятий собственных и смежных сопротивлений и контурных ЭДС, то уравнения выглядели бы так:

I 11·(R1 + R2 + R5) - I22·R2 - I 33·R5 = E1 - E 2,

-I 11 · R2 + I22· (R2 + R3 + R4) - I33·R4 = E2 + E3,

- I 11 · R 5 - I 22 · R 4 + I 33 · ( R 4 + R 5 + R 6) = 0.

В некоторых случаях такая запись даже более наглядна. Решение системы трех уравнений несложно провести и вручную. Значения контурных токов оказались равными:

I 11 = 1,289 А, I22 = 0,972 А, I33 = 0,768 А.

Теперь находим значения силы токов в ветвях:

I1= I11 = 1,289 A ,          I3 = -I22 = -0,972 A , I6 = I33 = 0,768 A,

I2= I 22 - I11 = -0,317 А , I4 = I22 - I33 = 0,204 A , I5 = 0,521 A.

Полученные значения токов совпадают с ранее полученными по законам Кирхгофа.

Метод узловых напряжений (или потенциалов)

Оставим ранее принятые условные положительные направления токов в ветвях. Направления обходов контуров нам теперь не понадобятся.

Обозначим цифрами номера узлов. Выберем точку нулевого потенциала в узле номер 4, т. е. положим   φ 4=0. Первый этап метода и главная его идея состоят в том, чтобы отыскать потенциалы остальных узлов: φ 1, φ2, φ3.

Введем новые обозначения. Будем называть сумму значений роводимостей всех ветвей, подходящих к К-му узлу, узловой проводимостью К-го узла и обозначать Gkk.

Сумму значений проводимостей всех ветвей, соединяющих два узла с номерами k и m, будем обозначать Gkm. Заметим, что в схемах нашего задания каждую пару узлов соединяет не более одной ветви, т. е. в нашем случае Gkm будет представлена всего одним членом.

Кстати, для обозначения потенциалов в учебниках часто используют буквы латинского алфавита V и U . Будем и мы обозначать потенциалы буквой V , оставив U для обозначения напряжений. Тогда потенциалы узлов у нас будут обозначены V 1, V 2, V 3 и V 4. Такая замена обозначений не носит принципиального характера. Просто при использовании ЭВМ на написание букв греческого алфавита, как правило, тратится больше времени, а при использовании разных программных инструментов могут встретиться и другие сложности. Кроме того, нам понадобится понятие узлового тока, представляющего собой алгебраическую сумму произведений значений проводимостей ветвей, подходящих к узлу на ЭДС соответствующих ветвей. Если ЭДС направлена от узла, произведение входит в эту сумму со знаком минус. Обозначать узловые токи будем J.

 

Итак:

Заметим, что:

Узловые токи:

Зададим произвольные начальные значения потенциалов для решения на MATHCAD методом итераций:

Запишем систему уравнений для узловых потенциалов и найдем значения:

Таким образом, мы определили потенциалы узлов в вольтах. Токи в ветвях будем искать по общей формуле:

Здесь I_km , V_km , R_km ток, ЭДС и сопротивление в ветви, соединяющей k -й и m -й узлы. При этом ЭДС E_km считается положительной, если направлена от k -го узла к m -му. В противном случае ее значение пишется со знаком «-». Если же ток оказался отрицательным, то это означает, что он переносит положительные заряды от m-го узла к k-му (или отрицательные в направлении, обозначенном нами стрелкой).

Итак:

I1=I41, I2=I31, I3=I21, I4=I24,  I5=I34, I6=I24.

 

Числовые значения, полученные по этим формулам:

Разумеется, здесь значения потенциалов приведены в вольтах, а значения силы токов в амперах.