 |
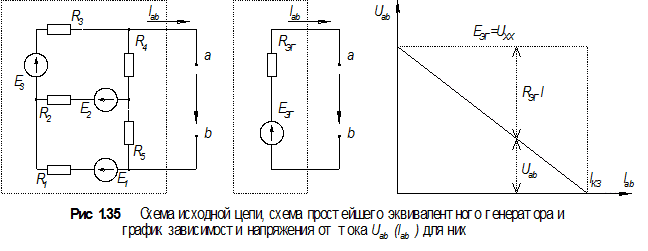
Метод состоит в том, что вся цепь, к которой подключается заданная ветвь (в нашем случае ветвь с сопротивлением R 6), заменяется всего двумя элементами: R эг и Еэг, которые называются сопротивлением, и ЭДС эквивалентного генератора соответственно. Если правильно подобрать эти элементы, то такая простейшая эквивалентная схема замещения цепи (рис. 1.35) ведет себя так же по отношению к выделенной ветви, как исходная, т. е. при тех же значениях сопротивления R 6 на нем выделится такое же значение напряжения и протечет такой же силы ток, как при включении R 6 в заданную исходную цепь.
Пунктиром на схемах (рис 1.35) показаны преобразуемый участок цепи (слева) и преобразованный в эквивалентный генератор (см. средний рисунок).
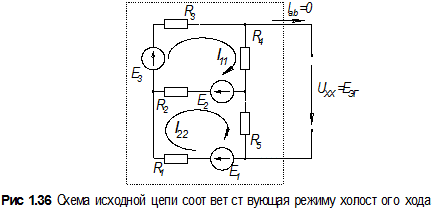 |
В теории [1] показано, что при постоянных сопротивлениях и ЭДС зависимость между током и напряжением U а b ( Iab ) имеет линейный характер, график этой зависимости – прямая линия. Так, что достаточно найти две точки на этой прямой, как можно будет определиться со всей зависимостью U а b ( Iab ) целиком. Выберем такие значения R 6, при которых нам будет легче рассчитать значения Еэг и R эг. Во-первых, это случай холостого хода, когда R 6 равно бесконечности или, попросту, обрыв шестой ветви. Ток I 6 = Iab при этом не пойдет вовсе (он будет равен нулю), а схема упростится до двухконтурной.
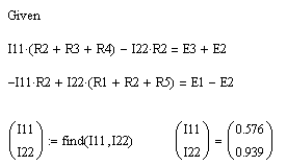 |
Как видим, при этом не будет тока и через сопротивление Rab , или в нашем случае R 6 , напряжение Uab станет равным Uxx= Еэг. Его-то мы и найдем из упрощенной схемы, превратившейся в двухконтурную. Уравнения, составленные по методу контурных токов для нее, выглядят так:
Отсюда ток I 11_хх = 0,576 А, а I 22 _хх = 0,939 А.
Дополнительные индексы контурных токов хх показывают, что это не те токи, которые ранее протекали в этих контурах до исключения из исходной схемы сопротивления R 6.
Значение напряжения холостого хода (или что то же Eэг) равно:
Uab _ xx = R 4⋅I 11 _xx + R5⋅I 22_xx = 25⋅0,576 + 5⋅0,939 = 19,1 В.
Кстати, имея доступ к решению систем уравнений на ЭВМ, например в среде MATHCAD, Exel или Тсalk, можно воспользоваться заготовкой системы уравнений для расчета методом узловых напряжений, которая уже составлена и даже записана на соответствующей странице и, положив в ней проводимость шестой ветви равной нулю, решить систему заново и получить значение
Uab _ xx = V 2_хх.
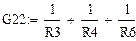 | |||
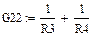 | |||
Итак, заменим на
 |
Как видим, V 2 хх стало равным 19,1 В, т. е. то же, что и рассчитанное предыдущим способом.
Rэг можно рассчитать как сопротивление обведенной пунктиром части исходной схемы между точками a и b (или что то же между точками 2 и 4 в обозначениях, использованных в методе узловых потенциалов).
Для этого надо положить равными нулю все ЭДС и, например, методом преобразования рассчитать сопротивление между точками a и b получившейся мостовой схемы, преобразовав предварительно треугольник сопротивлений R 2, R 3, R 4 в эквивалентную звезду.
Мы же для примера воспользуемся расчетом режима короткого замыкания, т.е. положим R 6 = 0 и найдём значение силы тока через него, в этом случае
I6 кз = I33 кз.
 Итак:
Итак:
Решив подновленную систему (вернее, с подновленными данными), получаем для I 33 кз значение 1,286 А.
Такой же силы ток короткого замыкания должен проходить и в упрощенной цепи с эквивалентным генератором при R 6 =0, если она действительно эквивалентна исходной. Но в этом случае:
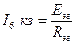 | 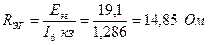 |
, откуда
Теперь, подставив найденные значения Еэг и R эг в выражение для тока в преобразованной цепи, найдем окончательно:
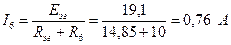 |
Итак, отличие от решения методом контурных токов или по законам Кирхгофа только в последнем знаке.
Конечно, предложенные вычисления I 6 методом эквивалентного генератора могут навести на мысль: «А зачем этот метод нужен, в чем же здесь выигрыш?». Ведь нам пришлось ради одного значения силы тока рассчитывать по ходу дела три режима цепи: холостой ход, короткое замыкание и только потом реальный ток в шестой ветви! Здесь надо сказать, что метод эквивалентного генератора выгоден не для одноразового расчета, как это задано в качестве учебного примера в этой РГР. Он выгоден для анализа поведения цепи при различных сопротивлениях R 6 . Ведь зная простейшую схему замещения реальной цепи (зная R эг и Еэг), по этой преобразованной схеме значительно легче предвидеть реакцию цепи на изменение R 6, а при случае и многократно просчитать вручную I 6 ( R 6 ). Это тем более удобно, важно и выгодно для цепей переменного тока, где расчет исходной сложной цепи достаточно громоздок.
Сравним результаты, полученные разными методами (см. таблицу 1.2).
Таблица 1.2
| I1, A | I2, A | I3, A | I4, A | I5, A | I6, A | Метод |
| 1,289 | -0,317 | -0,972 | 0,203 | 0.520 | 0,768 | Узловых напряжений |
| 1,289 | -0,317 | -0972 | 0,204 | 0,521 | 0,768 | Контурных токов |
| 1,289 | -0,317 | -0,972 | 0,203 | 0.520 | 0,768 | Законов Кирхгофа |
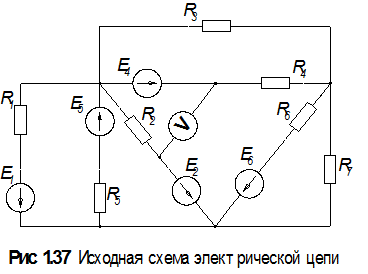 |
Пример 2
Параметры элементов схемы: R1=10 Ом, R2=8 Ом,
R3=20 Ом, R4= 5 Ом, R5=25 Ом, R6=50 Ом, R7=40 Ом,
E1=50 В, E2=40 В, E4=80 В, E5=120 В, E6=20 В.
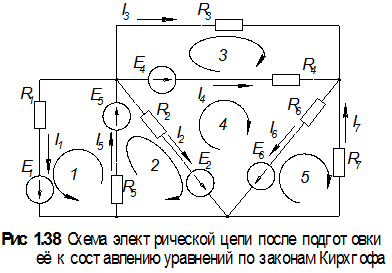 |
Составление системы уравнений по законам Кирхгофа
Прежде чем приступить к составлению уравнений по законам Кирхгофа, надо обязательно указать выбранные направления для токов, которые будем считать положительными и направления обходов контуров (см. рис. 1.38).
В этом примере не выдерживался принцип однообразия выбора обхода контуров. Часть из них обходятся по часовой, часть против часовой стрелки. Более того, в некоторых ветвях номера токов не совпадают с номерами сопротивлений и ЭДС. Всё это допустимо, однако заставляет внимательней следить за правильностью составления уравнений, что студент, видимо, почувствует сам, следя за изложением, и наученный этим опытом будет изначально стараться избегать таких выборов.
Система уравнений будет иметь вид:
| I1 | +I2 | +I3 | +I4 | -I5 | =0 | ||
| I3 | +I4 | -I6 | +I7 | =0 | |||
| R1I1 | +R5I5 | =E1+E5 | |||||
| R2I2 | +R5I5 | =E2+E5 | |||||
| R3I3 | -R4I4 | =-E4 | |||||
| -R2I2 | +R4I4 | +R6I6 | =-E2+E4+E6 | ||||
| -R6I6 | -R7I7 | =-E5 |
Система оказалась довольно громоздка, однако решение ее сразу дает значения искомых токов в ветвях. Вид у нее незаполненный из-за того, что члены, содержащие одинаковые неизвестные, записаны в разных уравнениях друг под другом.
В случае отсутствия члена с соответствующим неизвестным, оставлялось свободное место. Так потом легче составлять матрицу из коэффициентов и свободных членов: сразу видно, где проставлять нули.
Если подставить в нее числовые значения сопротивлений и ЭДС, в том числе и нулевые она будет выглядеть так:
| 1·I1 | +1·I2 | +1·I3 | +1·I4 | -1·I5 | +0·I6 | +0·I7 | =0 |
| 0·I1 | +0·I2 | +1·I3 | +1·I4 | +0·I5 | -1·I6 | +1·I7 | =0 |
| 10·I1 | +0·I2 | +0·I3 | +0·I4 | +25·I5 | +0·I6 | +0·I7 | =50+120 |
| 0·I1 | +8·I2 | +0·I3 | +0·I4 | +25·I5 | +0·I6 | +0·I7 | =40+120 |
| 0·I1 | +0·I2 | +20·I3 | -5·I4 | +0·I5 | +0·I6 | +0·I7 | =-80 |
| 0·I1 | -8·I2 | +0·I3 | +5·I4 | +0·I5 | +50·I6 | +0·I7 | =-40+80+20 |
| 0·I1 | +0·I2 | +0·I3 | +0·I4 | +0·I5 | -50·I6 | -40·I7 | =-120 |
Матрица коэффициентов и свободных членов выглядит так:
| 1 | 1 | 1 | 1 | -1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | -1 | 1 | 0 |
| 10 | 0 | 0 | 0 | 25 | 0 | 0 | 170 |
| 0 | 8 | 0 | 0 | 25 | 0 | 0 | 160 |
| 0 | 0 | 20 | -5 | 0 | 0 | 0 | -80 |
| 0 | -8 | 0 | 5 | 0 | 50 | 0 | 60 |
| 0 | 0 | 0 | 0 | 0 | -50 | -40 | -120 |
Первые семь столбцов этой матрицы составлены из коэффициентов при неизвестных токах, а последний столбец из правых частей (свободных членов) уравнений представленной выше системы.
Главный определитель системы, полученный из этой таблицы без последнего столбца, равен ∆ = -35 770 000.
Остальные по порядку ∆1 = -84 690 000, ∆2 = -61 150 000, ∆3 = 101 740 000,
∆4 = -165 280 000, ∆5 = -209 360 000, ∆6 = -36 180 000, ∆7 = 27 340 000.
Напомним, что остальные определители получаются из главного определителя путем подстановки столбца свободных членов вместо столбца с номером, равным номеру определителя.
Например, таблица для вычисления ∆1 выглядит так:
| 0 | 1 | 1 | 1 | 1 | -1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | -1 | 1 |
| 170 | 10 | 0 | 0 | 0 | 25 | 0 | 0 |
| 160 | 0 | 8 | 0 | 0 | 25 | 0 | 0 |
| -80 | 0 | 0 | 20 | -5 | 0 | 0 | 0 |
| 60 | 0 | -8 | 0 | 5 | 0 | 50 | 0 |
| -120 | 0 | 0 | 0 | 0 | 0 | -50 | -40 |
Вычисляем токи в ветвях:
I1 = ∆1/∆ = 2,367, I2 = ∆2/∆ = 1,709, I3 = ∆3/∆ = -2,845,
I4 = ∆4/∆ = 4,621, I5 = ∆5/∆ = 5,853, I 6 = ∆6/∆ = 1,011, I 7 = ∆7/∆ = -0,764.
Дата: 2018-12-28, просмотров: 962.