Разрушение происходи от излома по наклонному сечению от доминирующего действия изгибающего момента.

От действия М главные растягивающие напряжения достигают прочности бетона на растяжении 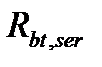, образуется трещина с max раскрытием в крайне растянутом нижнем сечении.

Бетон в сечении с трещиной из работы исключается, и растягивающее усилие воспринимает только арматура A_s и A_sw. Происходит поворот разделенных частей элемента относительно друг друга вокруг мгновенного центра вращения (точка О) - центра тяжести сжатой части. При этом плохо заанкерованная арматура A_s (мало 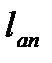п.333) плохо препятствует повороту, то есть напряжение в ней 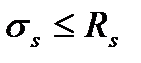, но она исключается из работы - выдергивается, сжатая зона сокращается и разрушается. При хорошей анкеровке арматура A_s препятствует повороту, и разрушение возможно, только если напряжения в ней достигнут R_s ( 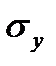или 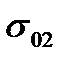) после этого деформации превысят , сечение поворачивается, сжатая зона сокращается, происходит разрушение.

Поэтому прочность наклонного сечения на действие момента обычно обеспечивается конструктивными мероприятиями повышающими длину анкеровки 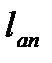. Если главные растягивающие напряжения не достигают R_bt , _ser., то трещина не образуется, соответственно нет трещины, нет поворота, нет разрушения. Прочность обеспечена бетоном.

Основное условие прочности имеет тот же вид, что и по нормальным сечениям 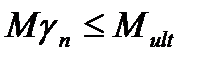(4.4).

                  (4.4)

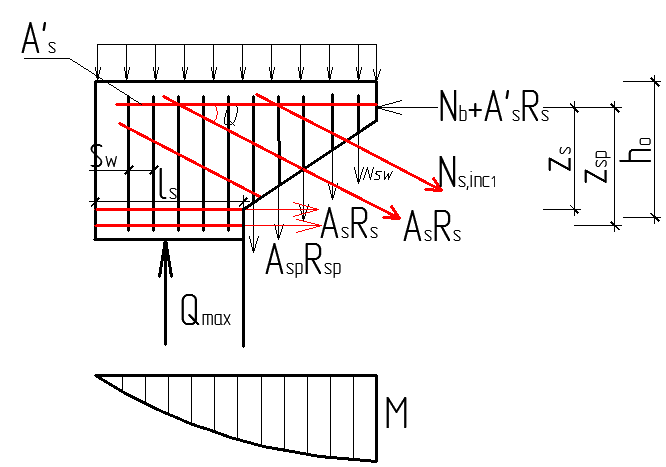В условии М-момент от всех внешних сил на участке элемента длиной равной проекции  относительно точки О.

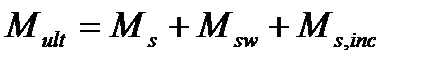        (4.63)

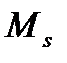 - момент воспринимаемый продольной арматурой A_s в наклонном сечении.

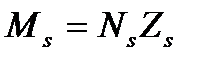                                              (4.64)

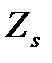 и 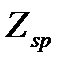 плечо внутренней пары определимое по формуле

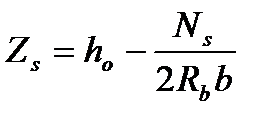                                        (4.65)

При наличии 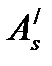 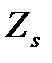принимается  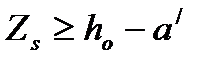и допускается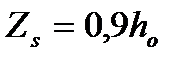

                           (4.66)

Если наклонное сечение пересекает продольную напрягаемую арматуру A_sp и не напрягаемую арматуру A_s без анкеров, то в формуле (4.66)

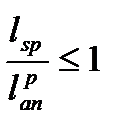и ,

где  и  - фактическая заделка соответственно A_sp и A_s за сечение.

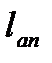 и 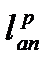 - требуемая длина анкеровки определяемая по формуле (3.9) и (3.11) при .

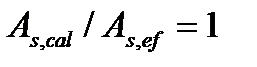Пр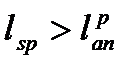и  или 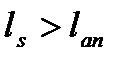, то есть сечение не перестает зону анкеровки, принимают:

                                         (4.67)

 - момент воспринимаемый хомутами.

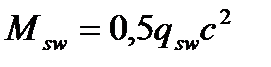   при 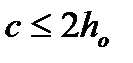                       (4.68)

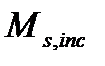- момент воспринимаемый отгибами.

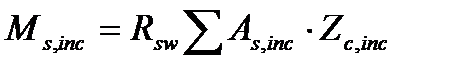 при           (4.69)

Расчет проводят в случае:

1) для сечений в местах обрыва продольной арматуры A_s.

2) у свободной опоры балок и концов консолей при отсутствии специальных анкеров.

3) 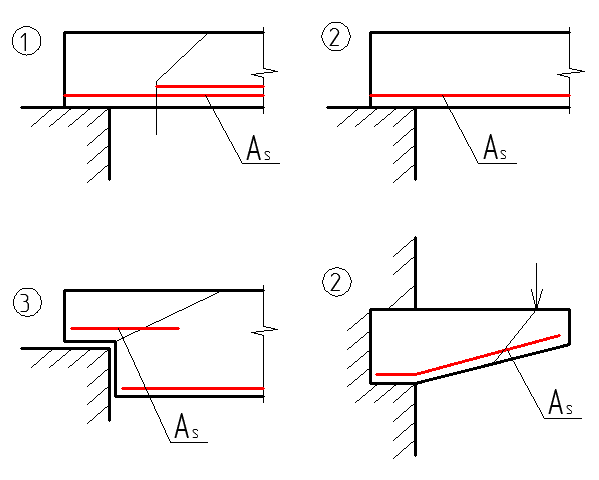сечения в местах резкого изменения высоты.

Длина проекции невыгодного наклонного сечения  начинающегося от опоры определяется.

А) при действии равномерно распределенной нагрузки :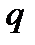

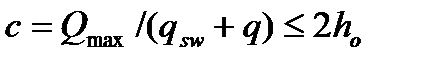        (4.70)

Б) при действии сосредоточенных сил принимается равным расстояниям до сил , а так же

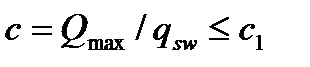
Во всех случаях: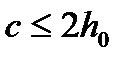

Если к арматуре A_s приваривается поперечная арматура A_sw или распределенная арматура, N_s по формуле (4.66), должно быть увеличено на:

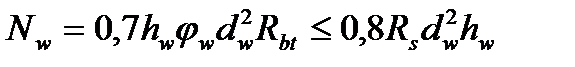                      (4.71)

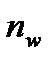 и 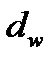 - количество и диаметр поперечных горизонтальных и вертикальных стержней на длине 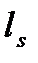,  коэффициент зависящий от 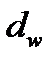.  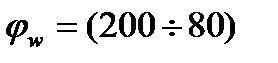при 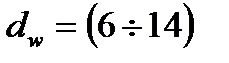 (табл. 3.4 СП 52-101)