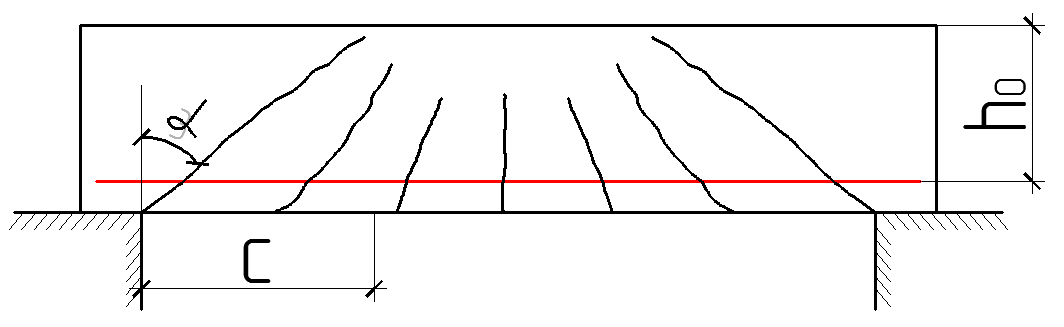
 В изгибаемых элементах по длине могут иметься сечения, в которых одновременно действуют два силовых фактора М и Q. Суммарное воздействие их в сечениях по длине элемента неодинаково, а трещины и расчетные сечения направлены перпендикулярно главным растягивающим усилиям. Ось, совпадающая с главным растягивающим напряжениям имеет наибольший наклон в сечении.
В изгибаемых элементах по длине могут иметься сечения, в которых одновременно действуют два силовых фактора М и Q. Суммарное воздействие их в сечениях по длине элемента неодинаково, а трещины и расчетные сечения направлены перпендикулярно главным растягивающим усилиям. Ось, совпадающая с главным растягивающим напряжениям имеет наибольший наклон в сечении.
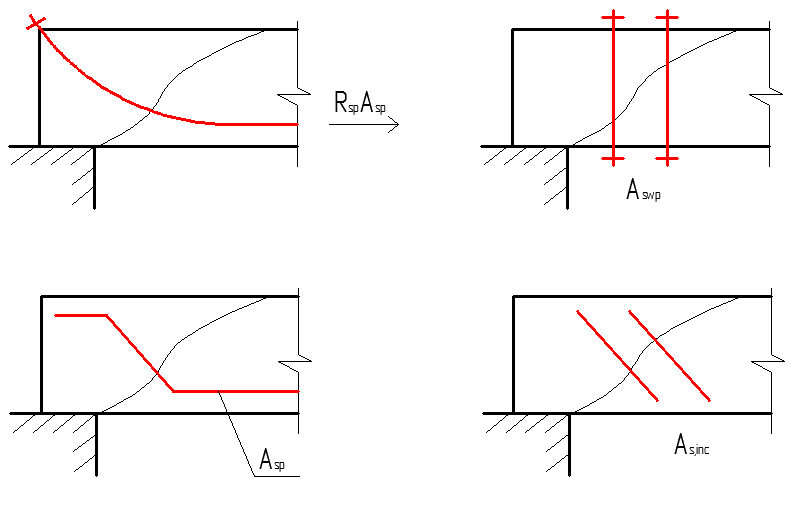 Сечения с высоким значением Q должны быть рассмотрены как наклонные, в которых может произойти исчерпание несущей способности. При этом напряжение в продольной арматуре Аs может быть значительно ниже Rs, т.к ее расположение относительно главных растягивающих напряжений, не дает возможности существенно влиять на работу сечения. Исчерпание несущей способности может произойти по бетону и поперечной арматуре (если она есть) в наклонном сечении (трещине) от действия Q и по наклонному сечению от действия M. Результат расчета сводится к определению достаточности несущей способности бетона и продольной арматуры для восприятия Q и M по наклонным сечениям. В случае если несущей способности бетона и As недостаточно устанавливают рабочую арматуру Asw. В отдельных случаях устанавливают Asw конструктивно, даже если она не требуется по расчету. См. п.5.18-5.28 СП 52-101-2003.
Сечения с высоким значением Q должны быть рассмотрены как наклонные, в которых может произойти исчерпание несущей способности. При этом напряжение в продольной арматуре Аs может быть значительно ниже Rs, т.к ее расположение относительно главных растягивающих напряжений, не дает возможности существенно влиять на работу сечения. Исчерпание несущей способности может произойти по бетону и поперечной арматуре (если она есть) в наклонном сечении (трещине) от действия Q и по наклонному сечению от действия M. Результат расчета сводится к определению достаточности несущей способности бетона и продольной арматуры для восприятия Q и M по наклонным сечениям. В случае если несущей способности бетона и As недостаточно устанавливают рабочую арматуру Asw. В отдельных случаях устанавливают Asw конструктивно, даже если она не требуется по расчету. См. п.5.18-5.28 СП 52-101-2003.
Для ограничения ширины раскрытия наклонных трещин применяют наклонную Аsinc, напрягаемую Аswp, отгиб части Аsp или Аs. Пн в любой арматуре не влияет на прочность наклонных сечений, т.к ПН в наклонной трещине при ее максимальном раскрытии полностью гасится ( кроме ПН обычной Asp в растянутой зоне), т.е она рассчитана на раскрытие нормальных трещин от действия максимального M, а не Q.
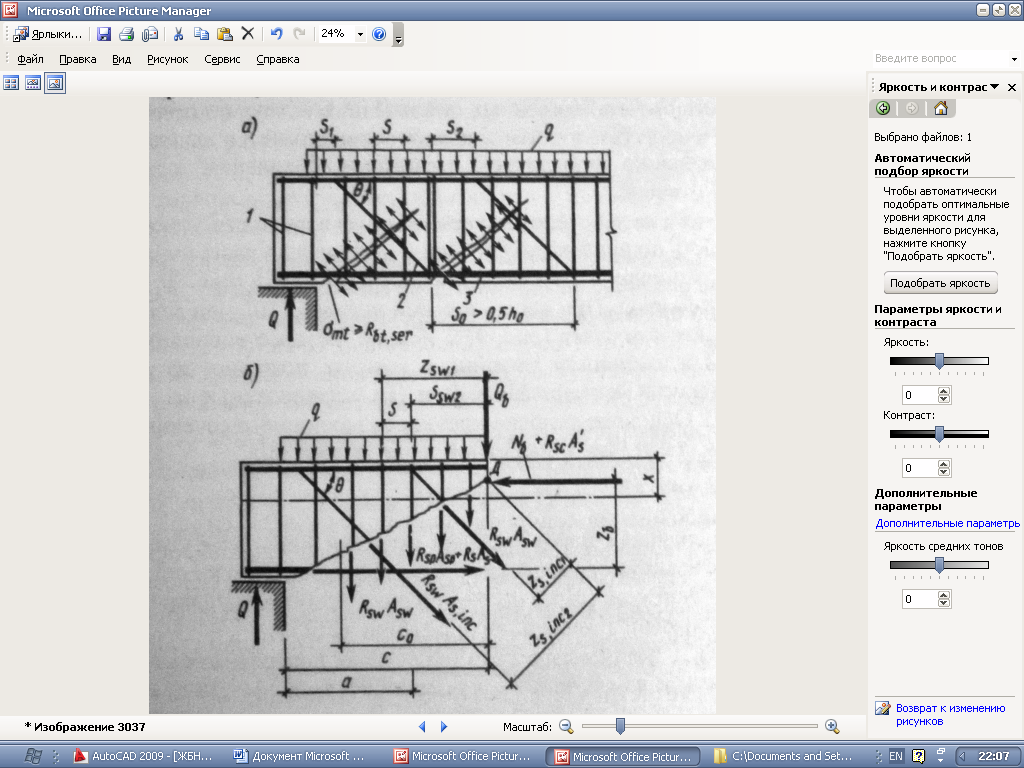
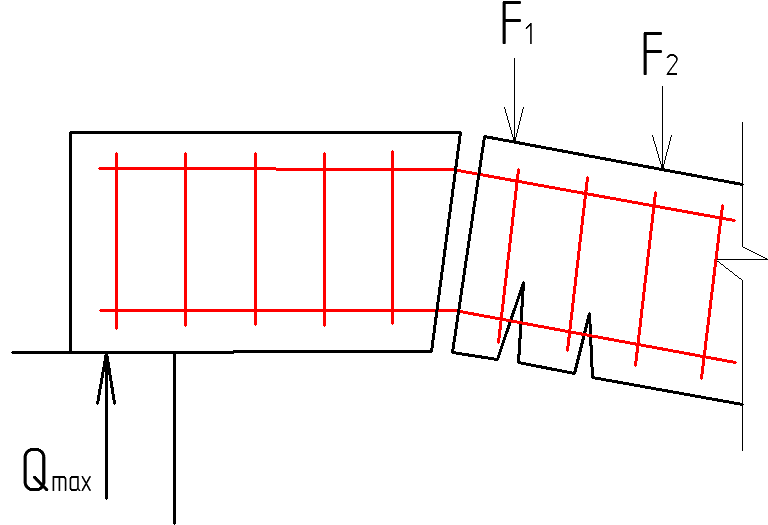 Разрушение по наклонному сечению от действия Q происходит от ее доминирующего действия. Вблизи границы Х (высоты) возникают максимальные касательные напряжения, и образуется трещина. Касательные напряжения распределяются равномерно по длине трещины, и она раскрывается одинаково по всей длине. Это возможно при хорошей анкеровке арматуры As, т. к она препятствует повороту в сечении одной части относительно другой.
Разрушение по наклонному сечению от действия Q происходит от ее доминирующего действия. Вблизи границы Х (высоты) возникают максимальные касательные напряжения, и образуется трещина. Касательные напряжения распределяются равномерно по длине трещины, и она раскрывается одинаково по всей длине. Это возможно при хорошей анкеровке арматуры As, т. к она препятствует повороту в сечении одной части относительно другой.
На уровне Х: 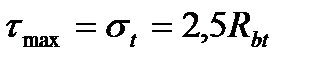 .
.
В сжатой зоне одновременно действует сжимающие и касательные напряжения. первые вызваны под действием М, вторые под действием Q.
При 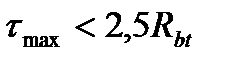 трещины не образуется и Q воспринимает бетон, в противном случае Asw – поперечная арматура.
трещины не образуется и Q воспринимает бетон, в противном случае Asw – поперечная арматура.
 4.2.2.1 Проверка прочности наклонных сечений при действии Q .
4.2.2.1 Проверка прочности наклонных сечений при действии Q .
Основное условие прочности имеет вид:
 , где (4.28)
, где (4.28)
Q – Поперечная сила в нормальном сечении проходящем через конец наклонного сечения с длиной проекции с, от действия сил приложенных за пределами длины с, с учетом
возможного отсутствия временной нагрузки на участке от опоры до с.
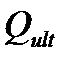 – несущая способность наклонного сечения
– несущая способность наклонного сечения
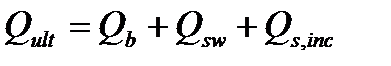 (4,29)
(4,29)
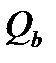 – поперечная сила воспринимаемая бетоном.
– поперечная сила воспринимаемая бетоном.
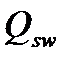 – поперечная сила воспринимаемая поперечными стержнями, попавшими в сечение длиной
– поперечная сила воспринимаемая поперечными стержнями, попавшими в сечение длиной 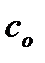 .
.
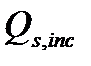 – поперечная сила воспринимаемая наклонными стержнями, попавшими на участок наклонной трещины не более
– поперечная сила воспринимаемая наклонными стержнями, попавшими на участок наклонной трещины не более 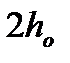 от ее конца.
от ее конца.
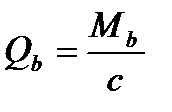 (4.30)
(4.30)
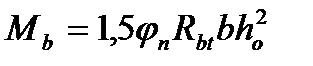 (4.31)
(4.31)
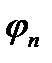 - коэффициент, учитывающий обжатие сечения ПН арматурой Аsp, сжатие при наличии сжимающих и растяжение при наличии растягивающих сил.
- коэффициент, учитывающий обжатие сечения ПН арматурой Аsp, сжатие при наличии сжимающих и растяжение при наличии растягивающих сил.
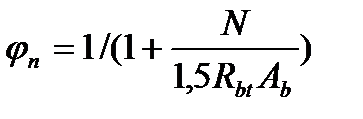 (4.32)
(4.32)
Растяжение, N- растягивающая сила,  .
.
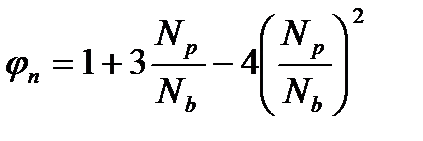 (4.32)
(4.32)
При сжатии и ПН Asp.
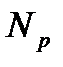 - усилие сжатия при центральном или внецентренном сжатии,
- усилие сжатия при центральном или внецентренном сжатии,
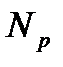 = 0,7P при ПН арматуре Аsp, где P – усилие ПН с учетом всех потерь, то есть
= 0,7P при ПН арматуре Аsp, где P – усилие ПН с учетом всех потерь, то есть 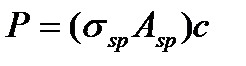 .
.
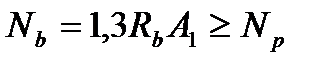 ;
;
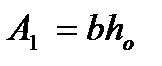 - без учета свесов таврового сечения.
- без учета свесов таврового сечения.
Коэффициент 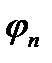 может быть определен следующей формулой:
может быть определен следующей формулой: 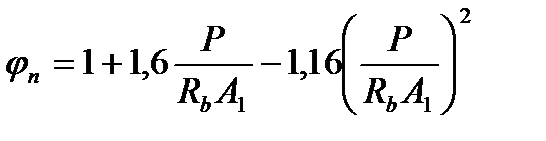 (4.34)
(4.34)
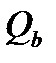 принимается не более
принимается не более 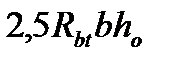 при
при 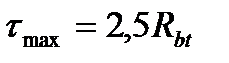 и не менее
и не менее
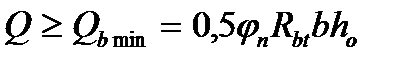 (4.35)
(4.35)
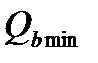 - это минимальная сила Q воспринимаемая бетоном при длине наклонной трещины с, определяемая в зависимости от загружения элемента.
- это минимальная сила Q воспринимаемая бетоном при длине наклонной трещины с, определяемая в зависимости от загружения элемента.
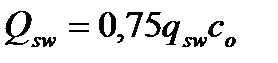 (4.36)
(4.36)
где 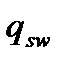 - интенсивность поперечного армирования или усилие в хомутах на единице длины, имеющая физический смысл распределенное по длине усилие в поперечной арматуре (размерность аналогична нагрузке q kH/м) Asw.
- интенсивность поперечного армирования или усилие в хомутах на единице длины, имеющая физический смысл распределенное по длине усилие в поперечной арматуре (размерность аналогична нагрузке q kH/м) Asw.
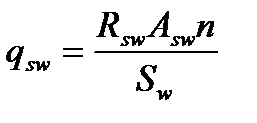 (4.37)
(4.37)
Rsw-расчетное сопротивление поперечной арматуры Аsw
Asw – площадь первого поперечного стержня.
n – количество рядов поперечных стержней(число стержней в первом сечении по длине)
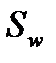 - шаг поперечной арматуры (см: п.п. 5.21 СП 52-101-2003).
- шаг поперечной арматуры (см: п.п. 5.21 СП 52-101-2003).

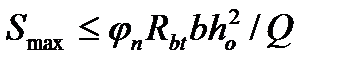 (4.38)
(4.38)
Величина 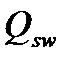 учитывается в уравнении (4.29) при выполнении условия:
учитывается в уравнении (4.29) при выполнении условия:
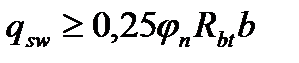 (4.39)
(4.39)
В противном случае Qsw = 0, кроме случая, когда 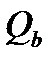 вычислен при условии (4.39) обращенный в равенство, т.е
вычислен при условии (4.39) обращенный в равенство, т.е  , (то есть заниженная прочность бетона на растяжение -
, (то есть заниженная прочность бетона на растяжение - 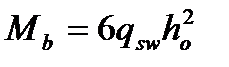 ;
; 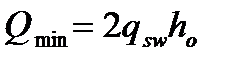 при
при 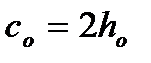 . где
. где  – участок проекции
– участок проекции  на котором расположены хомуты, учитываемые расчетом, то есть
на котором расположены хомуты, учитываемые расчетом, то есть  - это длина проекции опасной части проекции
- это длина проекции опасной части проекции  . Поэтому
. Поэтому  принимается:
принимается:

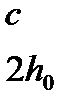 (4.40)
(4.40)
 Определение длины
Определение длины  .
.
В общем случае задаются для проверки (4.28) рядом возможных длин  , не превышающих расстояние до Mmax и не превышающих Сmax = 3h0.
, не превышающих расстояние до Mmax и не превышающих Сmax = 3h0.
При действии на элемент равномерно распределенной нагрузки 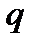 ,невыгодное значение
,невыгодное значение  :
:
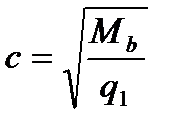
При 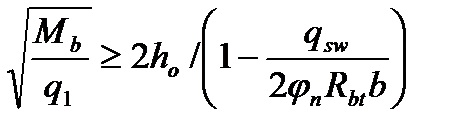 или
или 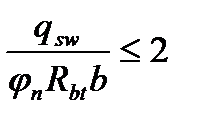 (4.41)
(4.41)
В противном случае: 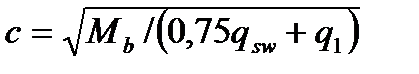 (4.42)
(4.42)
Принимают в формуле (4.41) 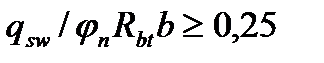 .
.
Условная нагрузка 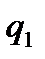 определяется:
определяется:
А) если расчетная нагрузка является сплошной, (то есть временная нагрузка тоже сплошная постоянная и сплошная, например бассейн-плита), то 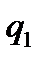 =
=  (4.43)
(4.43)
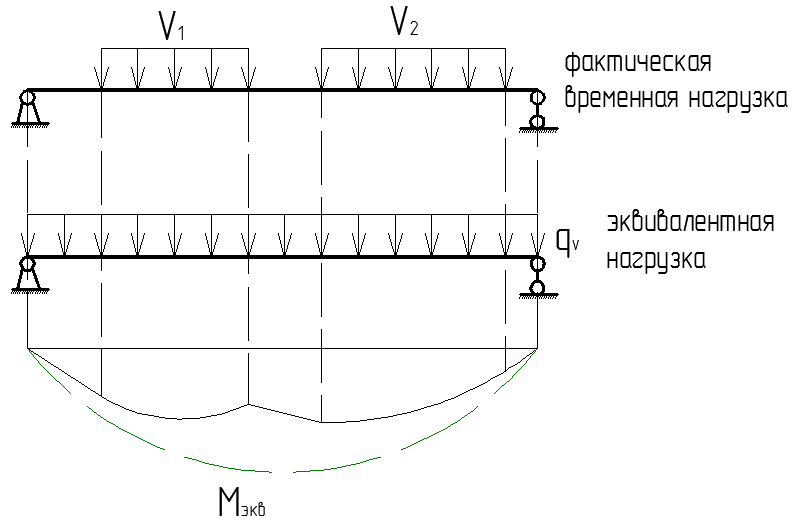 Б) если в нагрузку
Б) если в нагрузку 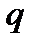 входят равномерная нагрузка
входят равномерная нагрузка 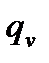 эквивалентная фактической/им временной/ым несплошной/м нагрузке/ам Vi по моменту, (т.е эп. от
эквивалентная фактической/им временной/ым несплошной/м нагрузке/ам Vi по моменту, (т.е эп. от 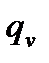 огибает эп. от любой Vi ).
огибает эп. от любой Vi ).
То учитывается отсутствие (возможное) временной фактической нагрузки на участке  от опоры и
от опоры и 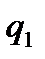 :
:
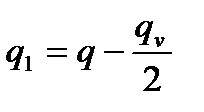 (4.44)
(4.44)
Так как это увеличит расчетную Q и уменьшит 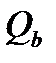 ; при этом значение Q в формуле (4.28) принимают
; при этом значение Q в формуле (4.28) принимают
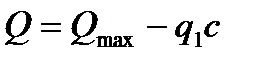 , (4.45)
, (4.45)
где  - поперечная сила в опорном сечении от нагрузки
- поперечная сила в опорном сечении от нагрузки 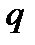 .
.
Б. При действии на элемент сосредоточенной силы F,  принимается равным расстояниям до сил
принимается равным расстояниям до сил 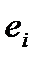 , но не менее
, но не менее 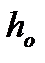 если
если 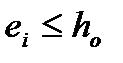 , а так же
, а так же
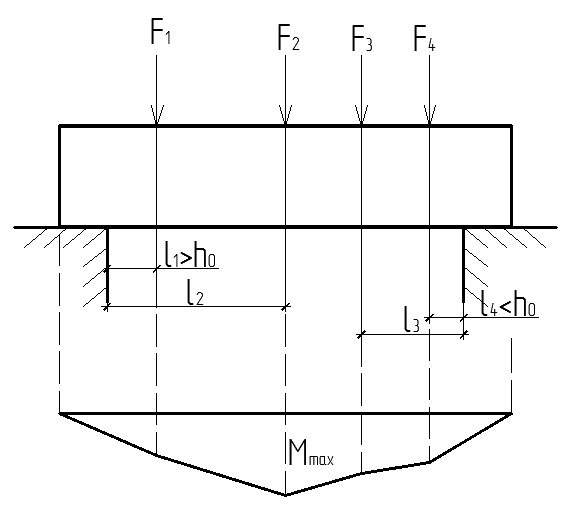
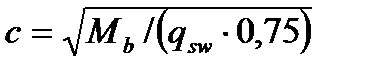 (4.46)
(4.46)
Дата: 2018-12-28, просмотров: 522.