Для решения многих практических задач часто бывает достаточно знать значения лишь нескольких характеристик (параметров) случайной величины, которые дают менее полное, но более наглядное представление об её распределении. Важнейшие из них: среднее (ожидаемое) значение, дисперсия и стандартное (среднее квадратичное) отклонение.
Среднее (ожидаемое) значение случайной величины
Концепция среднего широко используется практически во всех сферах человеческой деятельности. Средний возраст, средние объемы потребления, средняя заработная плата, средняя доходность – все это далеко не полный перечень показателей, ежедневно встречающихся в средствах массовой информации. Концепция среднего не только полезна, но и интуитивно понятна. Говоря о средних величинах, часто используют термин «ожидаемое значение».
Средним, или ожидаемым, значением (математическим ожиданием) дискретной величины Е называется сумма произведений ее значений на их вероятности:
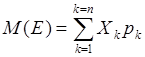
Выделяют следующие свойства этого показателя:
1. постоянный множитель С можно выносить за знак математического ожидания:
М(СЕ)=СМ(Е)
2. математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
M(E+G)= M(E)+M(G)
3. математическое ожидание постоянной величины С равно этой величине:
М(С) = С
4. математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
M(E*G) = M(E)*M(G)
В случае равной вероятности наступления каждого из событий математическое ожидание вычисляется как арифметическое среднее:
= 
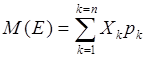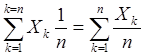
Математическое ожидание (среднее, или ожидаемое, значение) важнейшая характеристика случайной величины, так как служит центром распределения ее вероятностей.
Дисперсия и стандартное отклонение
Случайной величины
Дисперсия и стандартное отклонение служат характеристиками разброса (вариации) случайной величины от ее центра распределения (среднего значения М(Е)). Необходимость и полезность применения этих показателей хорошо иллюстрирует анекдот про математика, который свято верил в значимость средних величин и утонул в речке, средняя глубина которой не превышала половины его роста.
Дисперсией называется сумма квадратов отклонений случайной величины от ее среднего значения, взвешенных на соответствующие вероятности:
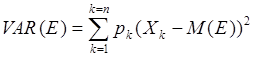
Отметим следующие свойства этого показателя:
1. Дисперсия постоянной величины равна 0
2. Для любой неслучайной постоянной С:
VAR(C+E) = VAR(E),
VAR(CE) = C2VAR(E)
Применение дисперсии не всегда удобно. Размерность дисперсии равна квадрату единицы измерения случайной величины.
На практике результаты анализа более наглядны, если показатель разброса случайной величины выражен в тех же единицах измерения, что и сама случайная величина. Для этих целей в качестве меры разброса случайной величины удобно использовать другой показатель – стандартное (среднее квадратическое) отклонение, рассчитываемое по формуле:
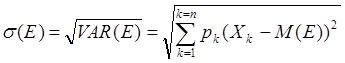
Отсюда следует, что величина s представляет собой средневзвешенное отклонение случайной величины от ее математического ожидания, при этом в качестве весов берутся соответствующие вероятности. Будучи выражено, в тех же единицах, стандартное отклонение показывает, насколько значения случайной величины могут отличаться от ее среднего.
Коэффициент вариации
Еще одним полезным показателем является коэффициент вариации, исчисляемый по формуле:
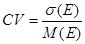
В отличие от стандартного отклонения коэффициент вариации – относительный показатель. В случае одинаковых или нулевых средних значений вычисление этого показателя теряет смысл. Очевидно, что при равных средних, чем больше величина стандартного отклонения s , тем больше коэффициент вариации. Помимо среднего значения и стандартного отклонения, асимметричные распределения часто требуют знания дополнительного параметра – коэффициента асимметрии (скоса).
2.4(4). Коэффициент асимметрии (скоса)
Коэффициент асимметрии (скоса) представляет собой нормированную величину и определяется по формуле:
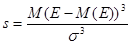
Коэффициент асимметрии может использоваться для приблизительной проверки гипотезы о нормальном распределении случайной величины. Его значение в этом случае должно быть равно 0.
Эксцесс
Некоторые симметричные распределения могут характеризоваться четвертым нормированным центральным моментом – эксцессом, вычисляемым по формуле:
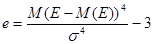
Если значение эксцесса больше нуля, кривая распределения более остроконечна, чем нормальная кривая. В случае отрицательного эксцесса кривая распределения более полога по сравнению с нормальной.
. Закон нормального распределения вероятностей
Нормальное распределение широко используется в различных сферах человеческой деятельности для приближенного описания случайных явлений, так как требует знания всего двух параметров среднего значения М(Е) и стандартного отклонения s(Е).
Случайная величина имеет нормальное распределение вероятностей с параметрами а и s ,если плотность ее распределения задается формулой:
, 
.
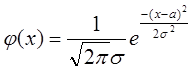
Математическое ожидание и дисперсия нормальной случайной величины Е соответственно равны а и s 2:
М(Е) = а VAR(E) = s 2
Нормальное распределение обладает рядом важнейших свойств:
· Вероятность больших отклонений нормальной случайной величины от центра ее распределения (параметра а) ничтожно мала;
· График функции плотности нормального распределения симметричен относительно средней (параметра а);
· Стандартное отклонениеs характеризует степень сжатия или растяжения графика функции плотности распределения вероятностей;
· Нормальная случайная величина Е с математическим ожиданием а и стандартным отклонением s с вероятностью близкой к 1 попадает в интервал :
(а-3s )<= E <=( a +3 s ) (правило трех сигм)
Закон нормального распределения вероятностей широко используется в процессе анализа рисков финансовых операций. Его важнейшие свойства, такие как симметричность распределения относительно средней, ничтожно малая вероятность больших отклонений значений случайной величины от центра ее распределения, правило 3-х сигм, позволяет существенно упростить проведение анализа и проведение сопутствующих расчетов.
Вид нормального распределения представлен на Рисунок 1. Нормальное распределение.
Рисунок 1. Нормальное распределение
 |
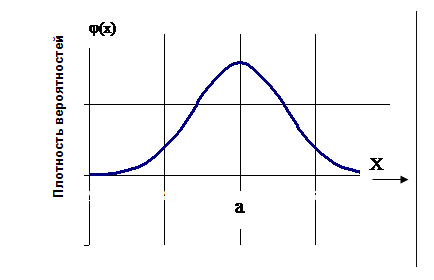Рисунок 2
Где а – математическое ожидание М(Е)
. Построение имитационной модели методом Монте-Карло
При вычислениях методом Монте-Карло статистические результаты получаются путем повторяющихся испытаний. Вероятность того, что эти результаты отличаются от истинных не более, чем на заданную величину, есть функция количества испытаний.
В основе вычислений по методу Монте-Карло лежит случайный выбор чисел из заданного вероятностного распределения. При практических вычислениях эти числа берут из таблиц или получают путем некоторых операций, результатами которых являются псевдослучайные числа с теми же свойствами, что и числа, получаемые путем случайной выборки. Имеется большое число вычислительных алгоритмов, которые позволяют получить данные последовательности псевдослучайных чисел.
Обозначим P{} теоретическое распределение, для которого мы хотим генерировать последовательность случайных чисел. Для любого отрезка [a,b] по определению P{[a,b]} равно вероятности того, что случайная величина, подчиняющаяся данному распределению, попадет в отрезок [a,b].
Пусть N количество чисел в последовательности, полученной с помощью датчика случайных чисел. Обозначим PN{} соответствующее эмпирическое распределение. ( По определению,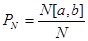 
, где N[a,b] количество чисел последовательности, попавших в отрезок [a,b].) Если последовательность случайных чисел распределена в соответствии с теоретическим распределением P{} , то для любого отрезка [a,b] при достаточно большом количестве N чисел в последовательности имеет место приблизительное равенство PN{[a,b]}= P{[a,b]}. (В пределе должно выполняться строгое равенство lim PN{[a,b]}= P{[a,b]}
N®¥
Покажем, каким образом, зная теоретические распределения входных параметров модели, можно построить эмпирическое распределение выходного параметра.
Пусть модель задана в виде Y=f (X1, X2,…. Xm). На основании известных теоретических распределений входных параметров X1, X2,…. Xm для каждого входного параметра Xk с помощью датчика случайных чисел строится последовательность чисел Xk1, Xk2,…. XkN, подчиняющаяся соответствующему теоретическому распределению. Затем с помощью последовательностей Xk1, Xk2,…. XkN , k=1,m ,строится последовательность чисел Y1,Y2, Y N для выходного параметра Y по формуле Yj=f(X1j, X2j,…. Xmj), где j=1,N.
Полученная последовательность Y1,Y2, Y N естественным образом задает эмпирическое распределение выходного параметра Y.
Дата: 2019-02-02, просмотров: 280.
