Часть 1. Основы построения имитационных систем для принятия экономических решений

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

УДК

ББК

Имитационное моделирование: Курс лекций. Часть 1. Сост: :А.М. Сидоренко, О.А. Дыкман, А.М. Якушева, Ю.С. Усова. - Н.Новгород: НКИ, 2002.- с. 113

Курс лекций предназначен для студентов НКИ, обучающихся по специальности «Прикладная информатика в экономике»

ББК

Нижегородский коммерческий институт, 2002

Составление, Сидоренко А.М.

Дыкман О.А.

Якушева А.М.

Усова Ю.С., 2002

Содержание

ВВЕДЕНИЕ............................................................................................................................. 5

Часть 1. Основы построения имитационных систем для принятия экономических решений........................................................................................ 7

Глава 1. Применение имитационных систем в экономических исследованиях......... 7

1.1. Понятие экономико-математической модели........................................................ 7

1.2. Роль моделей в экономической теории и принятии решений............................ 7

1.3 Структура системы экономико-математических моделей и требования, предъявляемые к математическим моделям................................................................................................. 8

1.4. Классификация экономико-математических моделей......................................... 8

1.5. Основы разработки имитационных моделей....................................................... 10

1.6. Предпосылки использования имитационных систем в экономических исследованиях............................................................................................................................................... 15

1.7. Этапы конструирования имитационных систем................................................ 18

Глава 2. Статистическое имитационное моделирование, как метод анализа экономических систем...................................................................................................................................... 19

2.1. Основы вероятностных методов анализа и моделирования экономических систем 19

2.2. Случайные события. Понятие вероятности........................................................ 20

2.3. Случайные величины и законы их распределений............................................ 21

2.4. Числовые характеристики случайных величин................................................. 22

2.4(1). Среднее (ожидаемое) значение случайной величины.................................... 23

2.4(2). Дисперсия и стандартное отклонение.............................................................. 24

случайной величины...................................................................................................... 24

2.4(3). Коэффициент вариации..................................................................................... 25

2.4(4). Коэффициент асимметрии (скоса).................................................................... 25

2.4(5) Эксцесс................................................................................................................. 25

2.5 . Закон нормального распределения вероятностей........................................ 26

2.6 . Построение имитационной модели методом Монте-Карло........................ 27

Глава 3. Применение имитационных моделей в финансово-экономической сфере. 29

3.1.Основные понятия об инвестициях, инвестиционной политике на предприятии и методах оценки инвестиционных проектов................................................................................ 29

3.2. Инвестиции как денежные потоки, применение финансового моделирования для оценки денежных потоков............................................................................................................ 32

3.2(1). Косвенный метод................................................................................................ 33

3.2(2). Прямой метод...................................................................................................... 33

3.3. Основные показатели экономической оценки инвестиционных проектов, являющиеся базой для финансового моделирования....................................................................... 38

3.3(1). Чистая текущая (дисконтированная) стоимость.............................................. 39

3.3(2). Внутренняя норма прибыли (доходности)....................................................... 41

3.3(3). Индекс рентабельности...................................................................................... 44

3.4. Анализ альтернативных проектов, оценка инвестиций в условиях дефицита финансовых ресурсов.............................................................................................................................. 48

3.5. Применение финансового моделирования для анализа эффективности инвестиционных проектов в условиях инфляции..................................................................................... 52

Глава 4. Имитационное моделирование для анализа рисков инвестиционных проектов. 55

4.1. Общая концепция риска.......................................................................................... 55

4.2. Виды предпринимательского риска...................................................................... 57

4.3. Методы количественного анализа рисков инвестиционных проектов.......... 58

4.4. Метод корректировки нормы дисконта................................................................ 59

4.5. Анализ чувствительности критериев эффективности....................................... 60

4.6. Метод сценариев........................................................................................................ 61

4.7. Деревья решений....................................................................................................... 62

4.8. Метод Монте-Карло (имитационное моделирование)........................................ 63

4.9. Алгоритм метода имитации Монте-Карло........................................................... 64

Глава 5. Количественный анализ рисков инвестиционных проектов с использованием финансовых функций MS Excel......................................................................................... 73

5.1. Чистая текущая (дисконтированная) стоимость................................................ 73

5.2. Индекс рентабельности проекта (PI)..................................................................... 75

5.3. Внутренняя норма доходности (IRR)..................................................................... 75

Глава 6. Технология имитационного моделирования в среде MS Excel................... 79

6.1 Имитационное моделирование с применением функций MS Excel.................. 80

6.2 Имитация с инструментом генератор случайных чисел.................................... 89

6.3. Статистический анализ результатов имитации.................................................. 93

6.4 Инструмент анализа данных - Корреляция.......................................................... 94

6.5. Инструмент анализа данных - Описательная статистика................................ 97

Глава 7. Основы построения дискретных имитационных моделей........................... 98

7.1. Имитационная модель опроса прохожих.............................................................. 98

7.2. Имитационная модель управления запасами.................................................... 104

ЛИТЕРАТУРА.................................................................................................................... 109

ВВЕДЕНИЕ

Управление в современном мире становится все более трудным делом, поскольку организационная структура общества постоянно усложняется. Эта сложность объясняется характером взаимоотношений между различными элементами организаций и физическими системами, с которыми они взаимодействуют. Хотя эта сложность существовала давно, только сейчас приходит понимание ее истинного значения. Теперь становится очевидно, что изменение одной из характеристик системы может легко привести к изменениям или создать потребность в изменениях в других частях системы.

В связи с этим одним из наиболее важных и полезных орудий анализа сложных процессов и систем стало имитационное моделирование. Имитировать, согласно словарю Вебстера, значит "вообразить, постичь суть явления, не прибегая к экспериментам на реальном объекте".

По существу, каждая модель или представление вещи средствами, отличными от ее реального содержания есть форма имитации. Имитационное моделирование является весьма широким и недостаточно четко определенным понятием, имеющим очень большое значение для лиц, ответственных за создание и функционирование практически любых систем. Вместе с тем, сама идея имитационного моделирования проста и в то же время интуитивно привлекательна. Она дает возможность экспериментировать с системами (существующими или предлагаемыми) в тех случаях, когда делать это на реальном объекте практически невозможно или нецелесообразно. Каждый современный руководитель, если он хочет добиться максимальной эффективности своего предприятия, должен периодически обращаться к методам имитационного моделирования, потому что оно является наиболее универсальным методом исследования систем и количественной оценки характеристик их функционирования.

При имитационном моделировании динамические процессы системы-оригинала подменяются процессами, имитируемыми в абстрактной модели, но с соблюдением основных правил (режимов, алгоритмов) функционирования оригинала. В процессе имитации фиксируются определенные события и состояния или измеряются выходные воздействия, по которым вычисляются характеристики качества функционирования системы.

Имитационное моделирование позволяет рассматривать процессы, происходящие в системе, практически на любом уровне детализации. При этом в имитационной модели можно реализовать практически любой алгоритм управленческой деятельности или поведения системы. Кроме того, модели, которые допускают исследование аналитическими методами, также могут анализироваться имитационными методами. Все это служит причиной того, что имитационные методы моделирования в настоящее время становятся основными методами исследования сложных систем.

Случайной величины

Дисперсия и стандартное отклонение служат характеристиками разброса (вариации) случайной величины от ее центра распределения (среднего значения М(Е)). Необходимость и полезность применения этих показателей хорошо иллюстрирует анекдот про математика, который свято верил в значимость средних величин и утонул в речке, средняя глубина которой не превышала половины его роста.

Дисперсией называется сумма квадратов отклонений случайной величины от ее среднего значения, взвешенных на соответствующие вероятности:

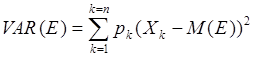
Отметим следующие свойства этого показателя:

1. Дисперсия постоянной величины равна 0

2. Для любой неслучайной постоянной С:

VAR(C+E) = VAR(E),

VAR(CE) = C²VAR(E)

Применение дисперсии не всегда удобно. Размерность дисперсии равна квадрату единицы измерения случайной величины.

На практике результаты анализа более наглядны, если показатель разброса случайной величины выражен в тех же единицах измерения, что и сама случайная величина. Для этих целей в качестве меры разброса случайной величины удобно использовать другой показатель – стандартное (среднее квадратическое) отклонение, рассчитываемое по формуле:

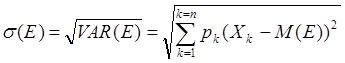
Отсюда следует, что величина s представляет собой средневзвешенное отклонение случайной величины от ее математического ожидания, при этом в качестве весов берутся соответствующие вероятности. Будучи выражено, в тех же единицах, стандартное отклонение показывает, насколько значения случайной величины могут отличаться от ее среднего.

Коэффициент вариации

Еще одним полезным показателем является коэффициент вариации, исчисляемый по формуле:

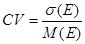
В отличие от стандартного отклонения коэффициент вариации – относительный показатель. В случае одинаковых или нулевых средних значений вычисление этого показателя теряет смысл. Очевидно, что при равных средних, чем больше величина стандартного отклонения s , тем больше коэффициент вариации. Помимо среднего значения и стандартного отклонения, асимметричные распределения часто требуют знания дополнительного параметра – коэффициента асимметрии (скоса).

2.4(4). Коэффициент асимметрии (скоса)

Коэффициент асимметрии (скоса) представляет собой нормированную величину и определяется по формуле:

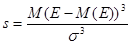
Коэффициент асимметрии может использоваться для приблизительной проверки гипотезы о нормальном распределении случайной величины. Его значение в этом случае должно быть равно 0.

Эксцесс

Некоторые симметричные распределения могут характеризоваться четвертым нормированным центральным моментом – эксцессом, вычисляемым по формуле:

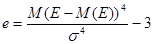
Если значение эксцесса больше нуля, кривая распределения более остроконечна, чем нормальная кривая. В случае отрицательного эксцесса кривая распределения более полога по сравнению с нормальной.

. Закон нормального распределения вероятностей

Нормальное распределение широко используется в различных сферах человеческой деятельности для приближенного описания случайных явлений, так как требует знания всего двух параметров среднего значения М(Е) и стандартного отклонения s(Е).

Случайная величина имеет нормальное распределение вероятностей с параметрами а и s ,если плотность ее распределения задается формулой:

, .

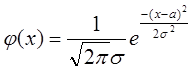
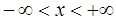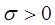Математическое ожидание и дисперсия нормальной случайной величины Е соответственно равны а и s ²:

М(Е) = а VAR(E) = s ²

Нормальное распределение обладает рядом важнейших свойств:

· Вероятность больших отклонений нормальной случайной величины от центра ее распределения (параметра а) ничтожно мала;

· График функции плотности нормального распределения симметричен относительно средней (параметра а);

· Стандартное отклонениеs характеризует степень сжатия или растяжения графика функции плотности распределения вероятностей;

· Нормальная случайная величина Е с математическим ожиданием а и стандартным отклонением s с вероятностью близкой к 1 попадает в интервал :

(а-3s )<= E <=( a +3 s ) (правило трех сигм)

Закон нормального распределения вероятностей широко используется в процессе анализа рисков финансовых операций. Его важнейшие свойства, такие как симметричность распределения относительно средней, ничтожно малая вероятность больших отклонений значений случайной величины от центра ее распределения, правило 3-х сигм, позволяет существенно упростить проведение анализа и проведение сопутствующих расчетов.

Вид нормального распределения представлен на Рисунок 1. Нормальное распределение.

Рисунок 1. Нормальное распределение

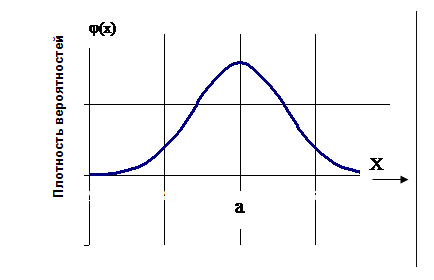Рисунок 2

Где а – математическое ожидание М(Е)

. Построение имитационной модели методом Монте-Карло

При вычислениях методом Монте-Карло статистические результаты получаются путем повторяющихся испытаний. Вероятность того, что эти результаты отличаются от истинных не более, чем на заданную величину, есть функция количества испытаний.

В основе вычислений по методу Монте-Карло лежит случайный выбор чисел из заданного вероятностного распределения. При практических вычислениях эти числа берут из таблиц или получают путем некоторых операций, результатами которых являются псевдослучайные числа с теми же свойствами, что и числа, получаемые путем случайной выборки. Имеется большое число вычислительных алгоритмов, которые позволяют получить данные последовательности псевдослучайных чисел.

Обозначим P{} теоретическое распределение, для которого мы хотим генерировать последовательность случайных чисел. Для любого отрезка [a,b] по определению P{[a,b]} равно вероятности того, что случайная величина, подчиняющаяся данному распределению, попадет в отрезок [a,b].

Пусть N количество чисел в последовательности, полученной с помощью датчика случайных чисел. Обозначим P_N{} соответствующее эмпирическое распределение. ( По определению, 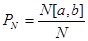, где N[a,b] количество чисел последовательности, попавших в отрезок [a,b].) Если последовательность случайных чисел распределена в соответствии с теоретическим распределением P{} , то для любого отрезка [a,b] при достаточно большом количестве N чисел в последовательности имеет место приблизительное равенство P_N{[a,b]}= P{[a,b]}. (В пределе должно выполняться строгое равенство lim P_N{[a,b]}= P{[a,b]}

N®¥

Покажем, каким образом, зная теоретические распределения входных параметров модели, можно построить эмпирическое распределение выходного параметра.

Пусть модель задана в виде Y=f (X₁, X₂,…. X_m). На основании известных теоретических распределений входных параметров X₁, X₂,…. X_m для каждого входного параметра X_k с помощью датчика случайных чисел строится последовательность чисел X_k₁, X_k₂,…. X_kN, подчиняющаяся соответствующему теоретическому распределению. Затем с помощью последовательностей X_k₁, X_k₂,…. X_kN , k=1,m ,строится последовательность чисел Y₁,Y₂, Y _N для выходного параметра Y по формуле Y_j=f(X₁_j, X₂_j,…. X_mj), где j=1,N.

Полученная последовательность Y₁,Y₂, Y _N естественным образом задает эмпирическое распределение выходного параметра Y.

Основные понятия об инвестициях, инвестиционной политике на предприятии и методах оценки инвестиционных проектов.

Согласно Федеральному закону " Об инвестиционной деятельности в РФ, осуществляемой в форме капитальных вложений" под инвестициями понимаются денежные средства, ценные бумаги, иное имущество, в том числе имущественные права, иные права, имеющие денежную оценку, вкладываемые в объекты предпринимательской и (или) иной деятельности в целях получения прибыли и (или) достижения иного полезного эффекта.

Инвестиции предполагают использование капитала для вложения в материальные активы или в ценные бумаги. В первом случае это могут быть вложения в основные фонды с длительными сроками амортизации (fixed capital investment). Это могут быть вложения в товарно-материальные запасы (inventory investment) или суммарные вложения в производственные фонды, включая землю (tоtа1 р1аnt investment). Во втором случае инвестиции называют финансовыми (financial investment). Ценные бумаги, как правило, это акции, облигации, векселя и др.

В качестве инвесторов могут выступать юридические или физические лица. Целью помещения их средств является прибыль или доход, прирост капитала или рост стоимости активов.

Вложения в материальные активы являются рискованными и не всегда возможными для большинства инвесторов с небольшим капиталом. Дело в том, что при строительстве или реконструкции дорогостоящих объектов прибыль на вложенный капитал не будет получена инвесторами до ввода этих объектов в эксплуатацию и расчетов этих объектов за полученные ссуды и проценты по ним.

Финансовые инвестиции также всегда связаны с определенным риском, поэтому вопрос определения эффективности инвестиций, как в материальные активы, так и финансовых имеют большое значение.

Важное значение имеет управление инвестициями на предприятии, которое находит свое отражение в инвестиционной политике фирмы.

Под инвестиционной политикой коммерческой организации следует понимать комплекс мероприятий, обеспечивающих выгодное вложение собственных, заемных и других средств в инвестиции, с целью обеспечения стабильной финансовой устойчивости работы предприятия в ближайшей и дальней перспективе.

Инвестиционная политика на предприятии должна вытекать из стратегических целей его бизнес-плана, т.е. из перспективного, а в конечном итоге она должна быть направлена на обеспечение финансовой устойчивости предприятия не только на сегодня, но и на будущее.

При разработке инвестиционной политики на предприятии необходимо придерживаться следующих принципов:

нацеленность инвестиционной политики на достижение стратегических планов предприятия и его финансовую устойчивость;

учет инфляции и фактора риска;

экономическое обоснование инвестиций;

формирование оптимальной структуры портфельных и реальных инвестиций;

ранжирование проектов и инвестиций по их важности и последовательности реализации исходя из имеющихся ресурсов и с учетом привлечения внешних источников;

выбор надежных и более дешевых источников и методов финансирования инвестиций.

Для решения всех этих задач на предприятии и должно использоваться финансовое моделирование.

Цель оценки инвестиционного проекта заключается в представлении информации лицу, принимающему решение, в виде позволяющем ему сделать вывод о целесообразности или нецелесообразности инвестирования. Для этого служит коммерческая (финансово-экономическая) оценка. Известны два основных подхода к оценке коммерческой привлекательности инвестиционного проекта: "финансовая состоятельность" (финансовая оценка) и экономическая оценка. Оба указанных подхода взаимно дополняют друг друга. В первом случае анализируется ликвидность проекта в ходе его реализации. Во втором - акцент ставится на потенциальной способности проекта сохранить покупательную ценность вложенных средств и обеспечить достаточный темп их прироста.

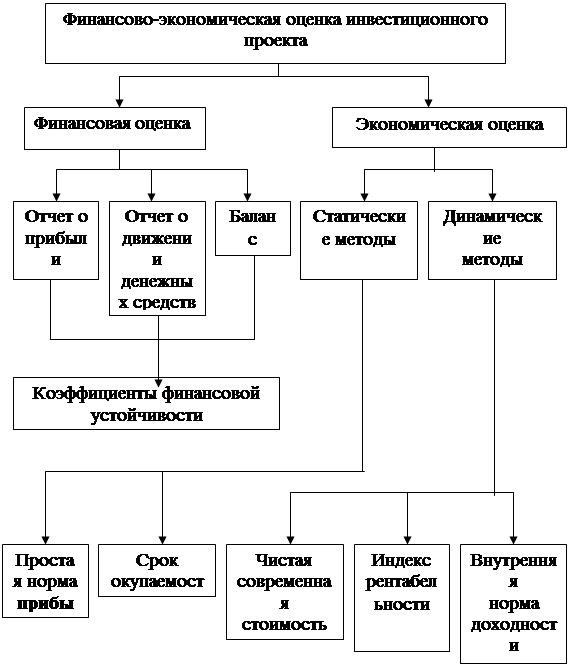
На рисунке 2 представлены некоторые из методов оценки по каждому из критериев.

Рисунок 2

Следует отметить, что помимо чисто формализованных, количественных методов, чрезвычайно важно учесть весь комплекс условий внешней и внутренней среды.

Косвенный метод

Чистая прибыль + Амортизационные отчисления + (—) Изменения в оборотном капитале = Чистый денежный поток от операционной деятельности.

Изменения в оборотном капитале представляют собой рост или сокращение значений: дебиторской и кредиторской задолженностей, стоимости производственных запасов, полученных авансов и других текущих активов и краткосрочных обязательств.

Прямой метод

Поступления от реализации продукции и услуг — Выплаты (производственные и другие операционные затраты) = Чистый денежный поток от операционной деятельности.

При формировании отчета о движении денежных средств прямым методом в статье «Выплаты (производственные и другие операционные затраты)» не должна учитываться сумма амортизационных отчислений. Понимание роли амортизационных отчислений как источника финансирования капитального ремонта и восстановления основных фондов предприятия является одним из самых распространенных и устойчивых заблуждений в российской практике финансового анализа. Тем более ошибаются те специалисты, которые считают, что амортизационные отчисления являются источником денежных средств для капитальных вложений.

Амортизационные отчисления относятся к особому типу затрат, которые называются калькуляционными. Само название типа затрат говорит о том, что амортизационные отчисления не приводят к реальному движению денежных средств. Величина этих затрат просто рассчитывается по определенным правилам, установленным законодательством. Единственный эффект, который дают амортизационные отчисления, — это изменение величины налогооблагаемой прибыли.

Однако при формировании отчета о движении денежных средств косвенным методом мы учитываем сумму амортизационных отчислений. Это объясняется очень просто. При расчете чистой прибыли как разницы между объемом продаж, прямыми производственными и общими расходами предприятия, а также налогами была уже учтена сумма амортизационных отчислений. Мы увеличиваем значение чистой прибыли на сумму амортизационных отчислений, чтобы компенсировать эту величину, которая фактически никуда не выплачивалась и ниоткуда не была получена предприятием.

Исторически в практике российских и зарубежных специалистов более распространен косвенный метод. Для анализа финансового состояния предприятия текущего и предыдущих периодов построение отчета денежных потоков косвенным методом не вызывает никаких проблем. Однако попытки применения косвенного метода для построения прогноза будущих денежных потоков, а именно эта задача стоит перед финансовыми аналитиками, оценивающими эффективность инвестиций и стоимость бизнеса, приводят к серьезным погрешностям и ошибкам.

Проблема состоит в том, что для построения отчета о движении денежных средств косвенным методом требуются исходные данные, полученные из отчета о прибылях и убытках (значение прибыли и амортизации), а также из баланса (изменения оборотного капитала).

Если вы прогнозируете деятельность предприятия, которое не предполагает существенных изменений; в своей деятельности, то это можно корректно сделать, используя историческую информацию.

Но большинство российских компаний представляют свои проекты, содержащие планы значительных изменений в своей деятельности: инвестиций для организации производства новых продуктов или услуг; изменений в системе продвижения и распределения продукции; реструктуризации предприятия, включая закрытие неприбыльных бизнес единиц и развитие прибыльных. Другими словами, подавляющее большинство российских компаний планируют изменения, которые можно отнести к революционным.

Попытки прогнозировать финансовое состояние такой компании с использованием только исторических данных теряют всякий смысл. Можно, используя финансовое моделирование, предсказать изменения в объеме продаж, издержках, амортизационных отчислениях и спрогнозировать величину прибыли, а также построить прогноз изменений текущих активов и краткосрочных обязательств, которые будут иметь место при изменении стратегии деятельности компании.

Построение прогноза отчета о движении денежных средств прямым методом является не чем иным, как моделированием реальных финансовых транзакций предприятия. Проанализируем на примерах отличия в отображении операций предприятия в различных финансовых отчетах.

Пример 1. Реализация продукции на сумму 1000 руб. в кредит на 100 дней (Таблица 3,4,5).

Пример 2. Реализация продукции на сумму 1000 руб. с предоплатой за 100 дней до поставки (Таблица 6,7,8).

Приведенные выше примеры наглядно демонстрируют, что первичным документом является не отчет о прибылях и убытках, а отчет о движении денежных средств. Отчет о движении денежных средств формируется в соответствии с условиями осуществления предприятием платежных операций и регистрирует события (платежные операции) только в тот период времени, когда эти события фактически происходят или должны произойти в будущем. При этом отчет о прибылях и убытках и баланс предприятия формируются в соответствии с общепринятыми правилами бухгалтерского учета. Другими словами, моделируя будущие платежные операции предприятия, мы делаем не что иное, как описываем движение денежных средств (Таблица 9).

Проблема выбора прямого или косвенного метода построения отчета о движении денежных средств нашла свое отражение в Международных стандартах финансовой отчетности ( IAS }. В Стандарте № 7 настоятельно рекомендуется применять при прогнозировании денежных потоков предприятия прямой метод построения отчета о движении денежных средств, так как использование косвенного метода для будущих периодов не позволяет получить корректные результаты.

Имеющиеся сегодня на рынке компьютерные системы финансового моделирования позволяют строить детальные корпоративные модели, адекватно описывающие финансовые операции предприятия без серьезных сложностей (Project Expert).

Таблица 3

Отчет о прибылях и убытках

(операции в кредит), руб.

Позиция

Период

1-й мес 2-й мес 3-й мес 4-й мес Объем продаж 1 000

Таблица 4


Баланс *(операции в кредит), руб.*
Позиция	Период
	1-й мес	2-й мес	3-й мес	4-й мес
Дебиторская задолженность Счет				1 000

Таблица 6


Отчет о прибылях и убытках *(операции с предоплатой), руб.*
Позиция	Период
	1-й мес	2-й мес	3-й мес	4-й мес
Объем продаж				1000

Таблица 7


Баланс *(операции с предоплатой), руб.*
Позиция	Период
	1-й мес	2-й мес	3-й мес	4-й мес
Дебиторская задолженность Счет	1000			1 000

Таблица 9

Пример отчета о движении денежных средств, Статья						Периоды
1	2	3	4	5
Поступления от реализации продукции		8000	10000	12000	14000
Выплаты на операционную деятельность		6000	7000	9000	10000
Денежный поток от операционной деятельности		2 000	3 000	3 000	4 000
Выплаты на приобретение активов	10000			2000
Поступления от реализации активов					1000
Денежный поток от инвестиционной деятельности	-10000			-2000	1 000
Поступления от размещения ценных бумаг	8000
Поступления в виде займов	4000
Выплаты в погашение займов			4000
Выплаты дивидендов			1 000	2000	2000
Денежный поток от финансовой деятельности	12 000		-5 000	-2000	-2000
Баланс наличности на начало периода	0	2000	4000	2000	1 000
Баланс наличности на конец периода	2 000	4 000	2 000	1 000	4 000

Для каждого отдельного инвестиционного проекта необходима информация об ожидаемых потоках наличности с учетом налоговых платежей.

Индекс рентабельности.

Индекс рентабельности ( profitability index - PI )

Метод расчета данного показателя является как бы продолжением метода расчета чистого приведенного дохода - NPV . Показатель PI в отличие от показателя NPV является относительной величиной.

Если инвестиции осуществлены разовым вложением, то данный показатель рассчитывается по формуле:

(6)

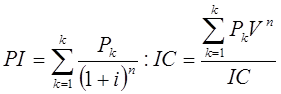
где Р _k — чистый доход;

I С— стартовые инвестиции;

Vⁿ — дисконтный множитель.

Если инвестиции представляют собой некоторый поток, то

(7)

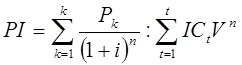
где I С— размеры инвестиционных затрат в периоды t = 1, 2,..., п.

Пример 6. Показатели современных величин вложений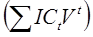

равны 5,1568 млн. руб., а современная величина чистых доходов составляет 5,4452 млн. руб.

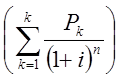
При этих условиях индекс рентабельности будет равен:

PI = 5,4452 / 5,1568 = 1,056(105,6%).

Если показатель Р I = 1, то это означает, что доходность инвестиции точно соответствует нормативу рентабельности (ставке сравнения).

При Р I < 1 инвестиции нерентабельны, так как не обеспечивают этот норматив.

3.3(4). Срок окупаемости инвестиций.

Срок окупаемости ( payback period method — РР) — один из наиболее часто применяемых показателей для анализа инвестиционных проектов.

Если не учитывать фактор времени, т.е. когда равные суммы дохода, получаемые в разное время, рассматриваются как равноценные, то показатель срока окупаемости можно определить по формуле:

(9)

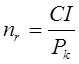
где n _у - упрощенный показатель срока окупаемости;

CI - размер инвестиций;

Р _k — ежегодный чистый доход.

Иначе говоря, период окупаемости (payback period ) — продолжительность времени, в течение которого не дисконтированные прогнозируемые поступления денежных средств превысят не дисконтированную сумму инвестиций, т.е. это число лет, необходимых для возмещения стартовых инвестиционных расходов.

Пример 3. Предположим, произведены разовые инвестиции в размере 38 тыс. руб. Годовой приток планируется равномерным в размере 10,7 тыс. руб.

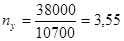года

Если же годовые поступления наличности не равны, то расчет окупаемости осложняется.

Предположим, что годовые притоки наличности распределены по годам следующим образом (см. Таблицу 12).

Таблица 12

Годы	1-й	2-й	3-й	4-й	5-й
Поступление наличности, тыс.руб.	8000	12000	12000	8000	8000

Сумма поступлений за первые 3 года составит:

8000 + 12 000 + 12 000 = 32 000 тыс. руб.,

т.е. из первоначальных инвестиции остается не возмещенными 38 000 — 32 000 = 6000 тыс. руб. Тогда при стартовом объеме инвестиций в размере 38 000 тыс. руб. период окупаемости составит:

3 года+ 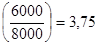года

Если рассчитанный период окупаемости меньше максимально приемлемого, то проект принимается, если нет — отвергается. Если бы в нашем примере необходимый период окупаемости был 4 года, проект был бы принят.

Более обоснованным является другой метод определения срока окупаемости. При использовании данного метода под сроком окупаемости — n_ok (РР) понимают продолжительность периода, в течение которого сумма чистых доходов, дисконтированных на момент завершения инвестиций, равна сумме инвестиций.

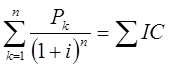
где Р _k — годовые доходы;

Σ IC — сумма всех инвестиций.

Пример 4. Инвестиционный проект характеризуется следующими членами потока платежей, которые относятся к концу года. Ставка процентов для дисконтирования принята 10%.

Таблица 13

Годы	1-й	2-й	3-й	4-й	5-й	6-й
Инвестиции, тыс.руб.	200	250	—	—	—	—
Отдача, тыс. руб.	—	—	150	250	300	300

Порядок решения

1этап. Для определения упрощенного срока окупаемости (Пу) суммируем годовые доходы и решим уравнение:

200+250 = 150+250+300х;

50 = 300х;

x=50/300=0,167

Из условия видно, что окупаемость наступит в период между четвертым и пятым годом, т.е. через 2 года после начала отдачи. Величина х= 0,167 характеризует часть года, в котором будет достигнута окупаемость. Следовательно, n _у = 2 + 0,167 = 2,167 года (2 года 61 день).

2 этап. Для оценки n_ok найдем сумму инвестиций с процентами по ставке i=10%.

ΣIС=200 · 1,1+ 250 = 470.

3 этап. За первые 2 года получения дохода их современная величина составит:

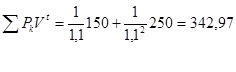
Т.е. эта величина меньше суммы инвестиции с начисленными процентами 342,97 < 470.

За 3 года современная величина дохода будет равна:

т.е. больше, чем стоимость инвестиций.

Отсюда срок окупаемости (при условии, что доход может выплачиваться и за часть года) составит:

n_ok= 2 + [(470 - 342,97) : 225,4] =2,56 года.

Величина 225,4 получена как 300 · 1,1^-3.

Рассмотрим определение срока окупаемости для доходов, которые можно представить в виде некоторых упорядоченных последовательностей (аннуитетов). Начнем с самого простого случая - с равномерного дискретного (один раз в конце года) поступления доходов. Из условий полной окупаемости за срок n_ok при заданной ставке i следует равенство суммы капитальных вложений современной стоимости аннуитета.

Аналогичным путем можно найти срок окупаемости для других видов распределения отдачи. В каждом таком случае капиталовложения приравниваются к современной величине финансовых рент, т.е. I С равно А, а члены денежного потока Р _k равны R - члену ренты (число членов потока в году — Р).

Пример 5. Инвестиции к началу поступления доходов составили 6 млн. руб., годовой доход ожидается на уровне 1,05 млн. руб., поступления ежемесячные, при принятой ставке сравнения i = 10%.

Исходя из формулы для расчета срока постоянных рент постнумерандо будет равно:

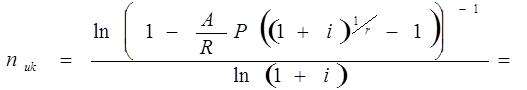
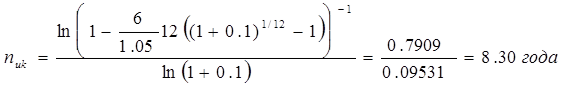
Для сравнения заметим, что без учета фактора времени получения доходов срок окупаемости составит n _у = 5,71 года (6 / 1,05 = 5,71) . Как видим, разница существенная.

Не всякий уровень дохода при прочих равных условиях приводит к окупаемости инвестиций.

Срок окупаемости существует, если не нарушаются определенные соотношения между поступлениями и размером инвестиций. Так, при ежегодном поступлении постоянных доходов (один раз в году) это соотношение имеет вид: Р _k > I С·i ; при поступлении постоянных доходов несколько раз в году (р - раз в году) Р _k > Р[(1 + i)^1/^p - 1] • I С;

при непрерывном поступлении доходов Р _k > In(1 + i ) IC .

Если перечисленные требования не выполняются, то капиталовложения не окупаются за любой срок, точнее, этот срок равен бесконечности.

Приведенные неравенства, вероятно, окажутся полезными для быстрой оценки ситуации.

Пример 6. i = 10%. Капиталовложения составляют 6 млн. руб., ожидаемая годовая отдача от инвестиций — 0,5 млн. руб. Исходя из приведенного неравенства, отдача должна быть больше, чем I С · i =0,1 • 6,0 = 0,6 млн. руб., но 0,5 < 0,6. Таким образом, при заданном уровне отдачи инвестиций не окупаются.

В то же время упрощенный срок окупаемости (без учета фактора времени) говорит о том, что инвестиции окупятся через 12 лет.

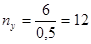
Основной недостаток показателя срока окупаемости n_ok как меры эффективности заключается в том, что он не учитывает весь период функционирования инвестиций и, следовательно, на него не влияет вся та отдача, которая лежит за пределами n_ok. Поэтому показатель срока окупаемости не должен служить критерием выбора, а может использоваться лишь в виде ограничения при принятии решения. То есть если срок окупаемости проекта больше, чем принятые ограничения, то он исключается из списка возможных инвестиционных проектов.

Общая концепция риска.

Концепция риска понятна. Его существование связано с невозможностью во многих случаях со 100% уверенностью прогнозировать будущее. Исходя из этого, следует выделить основное свойство риска: риск имеет место только по отношению к будущему и неразрывно связан с прогнозированием и планированием, а значит и с принятием решений вообще. Категории “риск” и “неопределенность” тесно связаны между собой и зачастую употребляются как синонимы. Однако между этими понятиями есть определённые различия.

Во-первых, риск имеет место только в тех случаях, когда принимать решение необходимо (если это не так, нет смысла рисковать).

Во-вторых, риск субъективен, а неопределённость объективна. Например, объективное отсутствие достоверной информации о потенциальном объёме спроса на производимую продукцию приводит к возникновению спектра рисков для участников проекта. Например, риск, порожденный неопределенностью вследствие отсутствия маркетингового исследования для инвестиционного проекта, обращается в кредитный риск для инвестора (банка, финансирующего этот проект), а в случае не возврата кредита в риск потери ликвидности и далее в риск банкротства, а для реципиента этот риск трансформируется в риск непредвиденных колебаний рыночной конъюнктуры.

Риск присутствует практически во всех сферах человеческой жизни, поэтому точно и однозначно сформулировать его невозможно, т.к. определение риска зависит от сферы его использования (например, у математиков риск – это вероятность, у страховщиков – это предмет страхования и т.д.). Неслучайно в литературе можно встретить множество определений риска.

В общем случае под риском понимают возможность наступления некоторого неблагоприятного события, влекущего за собой возникновение различного рода потерь (например, получение физической травмы, потеря имущества, получение доходов ниже ожидаемого уровня и т.д.).

Предпринимательская деятельность, осуществляемая в жестких условиях рыночной экономики, также не является исключением. Будет ли устойчивым спрос на новую продукцию? Какова будет стоимость акций через определенный промежуток времени? Сможет ли заемщик в срок вернуть кредит? Точные ответы на эти и многие другие вопросы часто не могут быть известны заранее. Риск бизнеса в условиях рынка – своеобразная плата за свободу предпринимательской деятельности.

В зависимости от степени детализации и выбранного подхода могут быть сформулированы различные определения предпринимательского риска. Так, в наиболее общем виде под риском понимают вероятность возникновения убытков или недополучения доходов по сравнению с прогнозируемым вариантом. Можно сформулировать и более детализированные подходы к определению этого понятия. В частности, риск может быть определен как уровень определенной финансовой потери, выражающейся:

а) в возможности не достичь поставленной цели;

б) неопределенности прогнозируемого результата;

в) субъективности оценки прогнозируемого результата.

Предпринимательский риск интерпретируется, как возможность отклонения фактических результатов проводимых операций от ожидаемых (прогнозируемых). Чем шире диапазон возможных отклонений, тем выше риск данной операции. При этом под результатом финансовой операции обычно понимают ее доходность (норму дохода), т.е. сумму полученных доходов, исчисленную в процентном отношении к сумме произведенных затрат.

Рассмотренный подход позволяет сформулировать важнейшее правило, на котором базируются стратегии принятия решений в условиях риска в сфере бизнеса. Оно заключается в следующем. Риск и доходность изменяются в одном направлении: чем выше доходность, тем, как правило, выше риск операции.

Принимая решения относительно проведения той или иной операции, финансовый менеджер обязан учитывать все возникающие при этом риски и их возможные последствия. В зависимости от объективных условий или субъективных предпочтений, основываясь на интуиции, здравом смысле или тщательном анализе имеющейся информации, он должен выбирать адекватную стратегию управления рисками, обеспечивающую достижение поставленных целей, например:

Минимизацию рисков при проведении операций;

Оптимизацию соотношений между степенью риска операции и возможными выгодами от ее проведения;

Компенсацию степени риска операции требованием более высокой нормы доходности и т.д.

Очевидно, что для того, чтобы иметь возможность выбора наименее рискованной операции, необходимо, прежде всего «измерить» степень ее риска, т.е. дать ему количественную оценку.

При оценке инвестиционных проектов большое значение играет фактор неопределенности, т.к. в течение срока реализации этого проекта могут произойти различные события, которые окажут воздействие на величину финансовых потоков по проекту.

Активы, с которыми ассоциируется относительно больший размер возможных потерь, рассматриваются как более рисковые. Возможна и другая интерпретация риска – как степени вариабельности дохода, который может быть получен благодаря владению данным видом активов. Так, государственные ценные бумаги обладают относительно небольшим риском, поскольку вариация дохода по ним практически равна нулю. Напротив, обыкновенная акция любой компании представляет собой значительно более рисковый актив, поскольку доход по такого рода акциям может ощутимо варьировать.

Иначе говоря, именно необходимость принимать решения в условиях неопределённости порождает риск, при отсутствии таковой необходимости нет и риска.

Метод сценариев

В отличие от трех предыдущих метод сценариев позволяет совместить исследование чувствительности результирующего показателя с анализом вероятностных оценок его отклонений. В общем случае процедура использования данного метода в процессе анализа инвестиционных рисков включает выполнение следующих шагов:

1. Определяют несколько вариантов изменений ключевых исходных показателей (например, пессимистический, наиболее вероятный и оптимистический).

2. Каждому варианту изменений приписывают его вероятностную оценку.

3. Для каждого варианта рассчитывают вероятное значение критерия NPV (либо IRR, РI), а также оценки его отклонений от среднего значения.

4. Проводится анализ вероятностных распределений полученных результатов.

Проект с наименьшими стандартным отклонением и коэффициентом вариации считается менее рисковым.

В целом метод позволяет получать достаточно наглядную картину для различных вариантов реализации проектов, а также предоставляет информацию о чувствительности и возможных отклонениях, а применение программных средств типа Excel позволяет значительно повысить эффективность подобного анализа путем практически неограниченного увеличения числа сценариев и введения дополнительных переменных.

Метод сценариев может быть легко реализован в среде EXCEL.

Деревья решений

Деревья решений обычно используются для анализа рисков проектов, имеющих обозримое или разумное число вариантов развития. Они особо полезны в ситуациях, когда решения, принимаемые в момент времени t = n, сильно зависят от решений, принятых ранее, и в свою очередь определяют сценарии дальнейшего развития событий.

Дерево решений имеет вид нагруженного графа, вершины его представляют ключевые состояния, в которых возникает необходимость выбора, а дуги (ветви дерева) - различные события (решения, последствия, операции), которые могут иметь место в ситуации, определяемой вершиной. Каждой дуге (ветви) дерева могут быть приписаны числовые характеристики (нагрузки), например, величина платежа и вероятность его осуществления. В общем случае использование данного метода предполагает выполнение следующих шагов:

1. Для каждого момента времени t определяют проблему и все возможные варианты дальнейших событий.

2. Откладывают на дереве соответствующую проблеме вершину и исходящие из нее дуги.

3. Каждой исходящей дуге приписывают ее денежную и вероятностную оценки.

4. Исходя из значений всех вершин и дуг рассчитывают вероятное значение критерия NPV (либо IRR, РI).

5. Проводят анализ вероятностных распределений полученных результатов.

Примеры

Предположим, что Вы хотите заняться ресторанным бизнесом. Вы оценили первоначальный взнос в 70 000 руб. и ожидаете получить чистый доход в течение пяти лет в следующих размерах: 12 000 руб., 15 000 руб., 18 000 руб., 21 000 руб. и 26 000 руб. Ячейки B1:B6 содержат следующие значения: -70 000, 12 000, 15 000, 18 000, 21 000 и 26 000 соответственно.

Следующая формула вычисляет внутреннюю скорость оборота инвестиции после четырех лет:

ВНДОХ(B1:B5) равняется -2,12 процентам

Внутренняя скорость оборота после пяти лет:

ВНДОХ(B1:B6) равняется 8,66 процентам

Чтобы вычислить внутреннюю скорость оборота после двух лет, придется задать аргумент прогноз:

ВНДОХ(B1:B3;-10%) равняется -44,35 процентам

Функция ЧИСТВНДОХ (платежи; даты; [прогноз])

Эта функция позволяет определить показатель IRR для потока платежей с произвольным распределением во времени, если известны их предполагаемые даты.

Пример

Рассмотрим инвестицию, при которой предполагается выплата наличными 10 000 руб. 1 января 2001 года и поступления: 2750 руб. 1 марта 2001 года, 4250 руб. 30 октября 2001 года, 3250 руб. 15 февраля 2002 года и 2750 руб. 1 апреля 2002 года. Внутренняя скорость оборота (в системе дат 1900) составит:

ЧИСТВНДОХ({-10000;2750;4250;3250;2750};
{"1.1.01";"1.3.01";"30.10.01";"15.2.02";"1.4.02"};0,1) равняется 0,374859 или 37,4859 процентам

К недостаткам IRR следует отнести нереалистичное предположение о ставке реинвестирования, так как предполагается реинвестирование получаемых доходов по ставке IRR, а это вряд ли осуществимо в реальной практике. Для корректного учета предположения о реинвестировании реализована функция МВСД.

Функция МВСД (платежи;ставка;ставка_реин)

Эта функция вычисляет модифицированную внутреннюю норму доходности – MIRR. Данная функция имеет специальный аргумент – предполагаемую ставку реинвестирования. Получаемая модифицированная норма рентабельности значительно ниже предыдущей, поэтому даже при более пессимистичной оценке реальных условий проект можно считать прибыльным.

Замечания

МВСД использует порядок расположения чисел в аргументе значения для определения порядка выплат и поступлений. Убедитесь, что значения выплат и поступлений введены в нужной последовательности и с правильными знаками (положительные значения для получаемых денег и отрицательные значения для выплачиваемых).

Если n - это количество чисел в аргументе значения, f - это ф_ставка, а r - это р_ставка, то формула для вычисления функции МВСД будет иметь вид:

Примеры

Предположим, что Вы занимаетесь рыболовным промыслом и только что завершили пятый год работы. Пять лет назад вы взяли 120 000 руб. под 10 процентов годовых для покупки лодки. Ваши годовые уловы принесли прибыль в 39 000 руб., 30 000 руб., 21 000 руб., 37 000 руб. и 46 000 руб. соответственно. За эти годы Вы реинвестировали получаемую прибыль под 12 процентов годовых. Пусть на рабочем листе Ваш заем введен как -120 000 в ячейку B1 и в ячейки B2:B6 введены значения Вашей прибыли за каждый год.

Тогда модифицированная внутренняя скорость оборота за пять лет вычисляется следующим образом:

МВСД(B1:B6; 10%; 12%) равняется 12,61 процентам

Модифицированная внутренняя скорость оборота за три года вычисляется следующим образом:

МВСД(B1:B4; 10%; 12%) равняется -4,80 процентам

Модифицированная внутренняя скорость оборота за пять лет, если значение аргумента р_ставка равно 14%, вычисляется следующим образом:

МВСД(B1:B6; 10%; 14%) равняется 13,48 процентам

Второй недостаток показателя внутренней нормы доходности связан с возможностью существования его нескольких значений. (В случае чередования притоков и оттоков наличности для одного проекта могут существовать несколько значений IRR). IRR является корнем функции n –ой степени , которая имеет n корней. Можно попытаться найти приемлемое значение IRR варьированием значений аргумента прогноз (от 0,1 до 0,9).

Синтаксис

СРЗНАЧ(значение1,значение2,…)

Значение1, значение2,… – это от 1 до 30 ячеек, интервалов ячеек или значений, для которых вычисляется среднее.

Функция ДИСПР()

Вычисляет дисперсию для генеральной совокупности.

Синтаксис

Функция СТАНДОТКЛОНП()

Вычисляет стандартное отклонение по генеральной совокупности. Стандартное отклонение – это мера того, насколько широко разбросаны точки данных относительно их среднего.

Синтаксис

СТАНДОТКЛОНП(число1; число2; …)

Число1, число2, … – это от 1 до 30 числовых аргументов, соответствующих генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

1. Логические значения, такие как ИСТИНА или ЛОЖЬ, а также текст игнорируются. Если текст и логические значения игнорироваться не должны, следует использовать функцию рабочего листа СТАНДОТКЛОНА.

Замечания

1. СТАНДОТКЛОНП предполагает, что аргументы образуют всю генеральную совокупность. Если данные являются только выборкой из генеральной совокупности, то стандартное отклонение следует вычислять с использованием функции СТАНДОТКЛОН.

2. Для больших выборок СТАНДОТКЛОН и СТАНДОТКЛОНП возвращают примерно равные значения.

3. Стандартное отклонение вычисляется с использованием «смещенного» или «n» метода.

Функции МИН() и МАКС() вычисляют минимальное и максимальное значения для массива данных из блока ячеек, указанного в качестве их аргумента. Функция СЧЕТЕСЛИ() осуществляет подсчет количества ячеек в указанном блоке, значения которых удовлетворяют заданному условию. Функция имеет следующий формат СЧЕТЕСЛИ (блок; «условие»). В данном случае заданная в ячейке F13 эта функция подсчитывает количество отрицательных значений NPV ,содержащихся в блоке ячеек ЧСС.

Функция СУММЕСЛИ() суммирует значения ячеек в указанном блоке, если они удовлетворяют заданному условию. Функция имеет следующий формат: СУММЕСЛИ (блок; «условие»). В данном случае заданные в ячейках F14,F15 функции подсчитывают суммы отрицательных и положительных значений NPV ,содержащихся в блоке ЧСС.

Две последние формулы (ячейки Е18 и F18) предназначены для проведения вероятностного анализа распределения NPV . В нашем примере мы исходим из предположения о независимости и равномерном распределении ключевых переменных Q,V,P . Однако какое распределение при этом будет иметь результирующая величина – показатель NPV - заранее определить нельзя.

Одно из возможных решений этой проблемы – попытаться аппроксимировать неизвестное распределение каким-либо известным. При этом в качестве приближения удобнее всего использовать нормальное распределение. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет распределение, приблизительно соответствующее нормальному. В прикладном анализе для целей аппроксимации широко применяется частный случай нормального распределения – так называемое стандартное нормальное распределение. Математическое ожидание стандартно распределенной случайной величины Е равно 0: М(Е) =0. График этого распределения симметричен относительно оси ординат и оно характеризуется всего одним параметром – стандартным отклонением s , равным 1.

Приведение случайной переменной Е к стандартно распределенной величине Z осуществляется с помощью, так называемой нормализации – вычитания средней и последующего деления на стандартное отклонение:

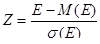
Величина Z выражается в количестве стандартных отклонений. Для вычисления вероятностей по значению нормализованной величины Z используются функции НОРМАЛИЗАЦИЯ() и НОРМСТРАСП()

Функция НОРМАЛИЗАЦИЯ (х; среднее; станд_откл)

Эта функция вычисляет нормализованное значение величины Х, на основании которого затем вычисляется искомая вероятность. Функция требует задания трех аргументов:

Х – нормализуемое значение;

Среднее – математическое ожидание случайной величины Е;

Станд_откл – стандартное отклонение

Полученное значение Z является аргументом для следующей функции НОРМСТРАСП()

Функция НОРМСТРАСП ( Z ) Эта функция вычисляет стандартное нормальное распределение, т.е. вероятность того, что случайная нормализованная величина Е будет меньше или равна Х. Она имеет всего один аргумент, вычисляемый функцией НОРМАЛИЗАЦИЯ().

Эти функции необходимо использовать вместе.

НОРМРАСП (НОРМАЛИЗАЦИЯ (Х; среднее; станд_откл)).

Приступаем к имитационному эксперименту. Для его проведения необходимо выполнить следующие шаги:

Ввести значения постоянных переменных в ячейки В2.В4 и D2.D4 листа «Результаты анализа».

Ввести значения диапазонов изменений ключевых переменных в ячейки В3.С5 листа «Имитация».

Задать в ячейке В7 требуемое число экспериментов.

Скопировать формулы блока А10.Е10 требуемое количество раз.

Перейти к листу «Результаты анализа» и проанализировать полученные результаты.

Рассмотрим реализацию выделенных шагов более подробно. Выполнение первых трех пунктов не должно вызвать особых затруднений. Введите значения постоянных переменных в ячейки В2.В4 листа «Результаты анализа». Введите значения диапазонов изменений ключевых переменных в ячейки В3.С5 листа «Имитация». Укажите в ячейке В7 число проводимых экспериментов, например – 500. Установите табличный курсор в ячейку А11.

На следующем шаге необходимо вставить в шаблон нужное количество строк (500) . Однако выделение такого количества строк при помощи указателя мыши – достаточно трудоемкая операция. EXCEL предоставляет более эффективные процедуры для выполнения подобных операций. В частности, в данном случае можно воспользоваться операцией перехода, которую также удобно применять и для выделения больших диапазонов ячеек.

Нажмите функциональную клавишу [F5]. На экране появится окно диалога «Переход» (Рисунок 8).

Рисунок 8. Окно диалога «Переход»

Для перехода к нужному участку электронной таблицы достаточно указать в поле «Ссылка» адрес или имя соответствующей ячейки (блока). В данном случае, таким адресом будет любая ячейка последней вставляемой строки. Например, в качестве адреса перехода может быть указана ячейка А508.

Введите в поле «Ссылка» адрес: А508 и нажмите комбинацию клавиш [SHIFT] + [ENTER]. Результатом выполнения этих действий будет выделение блока А10.А508.

Теперь необходимо заполнить вставленные строки формулами блока ячеек А10.Е10.

Результатом выполнения этих действий будет заполнение блока А10.Е509 случайными значениями ключевых переменных V, Q, P и результатами вычислений величин NCF и NPV. Фрагмент возможных результатов имитации приведен в Таблице19. Результат имитации

Таблица 19 Результат имитации

Исходные условия эксперимента

Минимум Максимум Перем.расходы 25 35 Количество 150 300 Цена 40 55 Экспериментов= 500 Номер стр.= 508 Переменные расходы (V) Количество (Q) Цена (P) Поступления (NCF) ЧСС (NPV) 26 155 45 1038 1 934,84 27 191 53 1846,4 4 999,31 32 235 54 1928 5 308,64 30 246 43 1139,2 2 318,46 35 280 55 2100 5 960,65 30 253 53 2187,6 6 292,73 26 192 54 2010,4 5 621,00 33 160 43 500 -104,61 34 167 40 260,8 -1 011,36 33 190 47 924 1 502,69 34 271 44 944 1 578,50 27 294 42 1624 4 156,24

Соответствующие проведенному эксперименту результаты анализа
приведены на рисунке 9.

Рисунок 9. Результат анализа

Результаты вероятностного анализа показывают, что шанс получить отрицательную величину NPV не превышает 7%. Еще больший оптимизм внушают результаты анализа распределения чистых поступлений от проекта NCF. Величина стандартного отклонения здесь составляет всего 42% от среднего значения. Таким образом с вероятностью более 90% можно утверждать, что поступления от проекта будут положительными величинами.

Сумма всех отрицательных значений NPV в полученной генеральной совокупности (ячейка F14) может быть интерпретирована как чистая стоимость неопределенности для инвестора в случае принятия проекта. Аналогично сумма всех положительных значений NPV (ячейка F15) может трактоваться как чистая стоимость неопределенности для инвестора в случае отклонения проекта. Несмотря на всю условность этих показателей, в целом они представляют собой индикаторы целесообразности проведения дальнейшего анализа.

Сумма всех отрицательных значений NPV в полученной генеральной совокупности (ячейка F14) может быть интерпретирована как чистая стоимость неопределенности для инвестора в случае принятия проекта. Аналогично сумма всех положительных значений NPV (ячейка F15) может трактоваться как чистая стоимость неопределенности для инвестора в случае отклонения проекта. Несмотря на всю условность этих показателей, в целом они представляют собой индикаторы целесообразности проведения дальнейшего анализа.

В данном случае они наглядно демонстрируют несоизмеримость суммы возможных убытков по отношению к общей сумме доходов (-11691,92 и 1692669,76 соответственно).

На практике одним из важнейших этапов анализа результатов имитационного эксперимента является исследование зависимостей между ключевыми параметрами. Методы оценки степени зависимости, а также технология ее автоматизации путем применения специальных инструментов ППП EXCEL, будут продемонстрированы ниже. Здесь же мы ограничимся визуальным (графическим) исследованием. На Рисунок 10 Распределение значений параметров V, P и Q приведен график распределения значений ключевых параметров V, P и Q, построенный на основании 75 имитаций.

Рисунок 10 Распределение значений параметров V, P и Q

Нетрудно заметить, что в целом, вариация значений всех трех параметров носит случайный характер, что подтверждает принятую ранее гипотезу о их независимости. Для сравнения ниже приведен график распределений потока платежей NCF и величины NPV (Рисунок 11. Зависимость между NCF и NPV.).

Рисунок 11. Зависимость между NCF и NPV .

Как и следовало ожидать, направления колебаний здесь в точности совпадают и между этими величинами существует сильная корреляционная связь, близкая к функциональной. Дальнейшие расчеты показали, что величина коэффициента корреляции между полученными распределениями NCF и NPV оказалась равной 1.

Подводя итоги, отметим, что в целом применение рассмотренной технологии проведения имитационных экспериментов – достаточно трудоемкий процесс, который к тому же ограничивается случаем равномерного распределения исследуемых переменных. Гораздо более удобным и эффективным способом решения таких задач является использование специального инструмента анализа – Генератор случайных чисел.

Синтаксис

НОРМРАСП(x;среднее;стандартное_откл;интегральная)

X - это значение, для которого строится распределение.

Среднее - это среднее арифметическое распределения.

Стандартное_откл - это стандартное отклонение распределения.

Интегральная –0 или 1

В зависимости от заданного параметра интегральная – 0 (ложь) или 1(истина) – она возвращает плотность распределения j (х) или значение функции распределения вероятностей F ( x ) для нормальной случайной величины.

Переходим к следующему листу и присваиваем ему имя Имитация2 . Первая часть этого листа ( блок ячеек А1:Е10) предназначена для ввода исходных данных и расчета необходимых параметров их распределений. Нормальное распределение характеризуется двумя параметрами - математическим ожиданием (средним) и стандартным отклонением. Для расчета стандартных отклонений используются формулы - массивы.

Функция СУММПРОИЗВ()

Перемножает соответствующие элементы заданных массивов и возвращает сумму произведений.

Синтаксис

СУММПРОИЗВ(массив1;массив2;массив3; ...)

Массив1, массив2, массив3, ... - это от 2 до 30 массивов, чьи компоненты нужно перемножить, а затем сложить.

· Аргументы, которые являются массивами, должны иметь одинаковые размерности. Если это не так, то функция СУММПРОИЗВ возвращает значение ошибки #ЗНАЧ!.

· СУММПРОИЗВ трактует нечисловые элементы массивов как нулевые.

Пример

	A	B	C	D	E
1	3	4		2	7
2	8	6		6	7
3	1	9		5	3
4

Следующая формула перемножает все компоненты двух массивов, а затем складывает полученные произведения, то есть выполняются следующие вычисления: 3*2 + 4*7 + 8*6 + 6*7 + 1*5 + 9*3.

СУММПРОИЗВ({3;4:8;6:1;9}; {2;7:6;7:5;3}) равняется 156

Для формирования листа Имитация 2 необходимо определить необходимые имена (Вставка-имя-присвоить) для блоков ячеек и задать требуемые формулы. Затем ввести исходные значения постоянных переменных, ввести значения ключевых переменных и соответствующие вероятности.

Устанавливаем курсор в ячейку Переменные расходы и . приступаем к проведению имитационного эксперимента.

· Выбрать в главном меню Сервис-Анализ данных. Результатом выполнения этих действий будет появление диалогового окна Анализ данных, содержащего список инструментов анализа.

· Выбрать из списка Инструменты анализа пункт Генерация случайных чисел.

· На экране появится диалоговое окно (Рисунок 12. Окно генерация случайных чисел). Указать в списке Распределения требуемый тип - Нормальное. Заполнить остальные поля окна.

Результатом будет заполнение блока ячеек (переменные расходы) сгенерированными случайными значениями.

Рисунок 12. Окно генерация случайных чисел

Первым заполняемым аргументом диалогового окна Генерация случайных чисел является поле Число переменных. Оно задает количество колонок ЭТ, в которых будут размещаться сгенерированные в соответствии с заданным законом распределения случайные величины. В нашем примере оно должно содержать 1 , т.к. ранее мы отвели под значения переменной V одну колонку - А. В случае, если указывается число больше 1, случайные величины будут размещены в соответствующем количестве соседних колонок, начиная с активной ячейки. Если это число не введено, то все колонки в выходном диапазоне будут заполнены.

Следующий обязательный аргумент для заполнения – содержимое поля Число случайных чисел (количество имитаций). Согласно условиям примера оно должно быть равно 500. При этом MS Excel автоматически подсчитывает необходимое количество ячеек для хранения генеральной совокупности.

Необходимый вид распределения задается путем соответствующего выбора из списка Распределения. Как уже отмечалось ранее, могут быть получены семь наиболее распространенных в практическом анализе типов распределений, каждое из которых характеризуется собственными параметрами. В рассматриваемом примере выбор типа распределения Нормальное повлек за собой появление дополнительных аргументов – параметров Среднее Стандартное отклонение, рассчитанных ранее для исследуемой переменной V листа Имитация. Эти аргументы могут быть заданы только в виде констант. Использование адресов ячеек и собственных имен здесь не допускается.

Указание аргумента Случайное рассеивание позволяет при повторных запусках генератора получать те же значения случайных величин, что и при первом. Таким образом, одну и ту же генеральную совокупность случайных чисел можно получить несколько раз, что значительно повышает эффективность анализа. В случае если этот аргумент не задан (равен 0), при каждом последующем запуске генератора будет формироваться новая генеральная совокупность. В нашем примере этот аргумент задан равным 1,что позволит нам оперировать с одной и той же генеральной совокупностью и избежать постоянных перерасчетов таблицы.

Последний аргумент диалогового окна Генерация случайных чисел – Параметры вывода определяет место расположения полученных результатов. При этом можно выбрать три варианта размещения:

Выходной блок ячеек на текущем листе (достаточно ввести ссылку на левую верхнюю ячейку выходного диапазона, при этом его размер будет определен автоматически и в случае возможного наложения генерируемых значений на уже имеющиеся данные на экран будет выведено предупреждающее сообщение;

Новый рабочий лист – в рабочей книге будет открыт новый лист, содержащий результаты генерации случайных чисел, начиная с ячейки А1;

Новая рабочая книга – будет открыта новая книга с результатами имитации на первом листе.

В рассматриваемом примере для проведения дальнейшего анализа необходимо, чтобы случайные величины размещались в специально отведенные для них блоки ячеек. В частности для хранения 500 значений первой переменной ранее был указан блок ячеек: Переменные расходы . Поскольку для этого блока определено собственное имя – Перем_расх, его необходимо указать в качестве выходного диапазона.

Генерация значений остальных переменных Q и Р осуществляется аналогичным образом.

По результатам проведенного имитационного эксперимента необходимо провести статистический анализ.

Рисунок 13. Анализ данных . Список инструментов анализа

Рисунок 14. Заполнение окна диалога инструмента Корреляция

Таблица 21. Результаты корреляционного анализа

	Переменные расходы (V)	Количество (Q)	Цена (P)	Поступления (NCF)	ЧСС (NPV)
Переменные расходы (V)	1
Количество (Q)	0,0527583	1
Цена (P)	0,0523678	-0,0611898	1
Поступления (NCF)	-0,394848848	0,548358	0,672387	1
ЧСС (NPV)	-0,394848848	0,548358	0,672387	1	1

Результаты корреляционного анализа представлены в виде квадратной матрицы (Таблица 21. Результаты корреляционного анализа), заполненной только на половину, поскольку значение коэффициента корреляции между двумя случайными величинами не зависит от порядка их обработки. Эта матрица симметрична относительно главной диагонали, элементы которой равны 1, так как каждая переменная коррелирует сама с собой.

Как следует из результатов корреляционного анализа, выдвинутая в процессе решения гипотеза о независимости распределений ключевых переменных V, Q, P в целом подтвердилась. Значения коэффициентов корреляции между переменными расходами V, количеством Q и ценой Р достаточно близки к 0.

В свою очередь величина показателя NPV напрямую зависит от величины потока платежей (R = 1). Кроме того, существует корреляционная зависимость средней степени между Q и NPV (R = 0,548), P и NPV (R = 0,67). Как и следовало ожидать, между величинами V и NPV существует умеренная обратная корреляционная зависимость (R = -0,39).

Полезность проведения последующего статистического анализа результатов имитационного эксперимента также в том, что во многих случаях он позволяет выявить некорректности в исходных данных либо даже ошибки в постановке задачи.

Следует отметить, что близкие к нулевым значения коэффициента корреляции R указывают на отсутствие линейной связи между исследуемыми переменными, но не исключает возможности нелинейной зависимости. Кроме того, высокая корреляция не обязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значений третьей.

При проведении имитационного эксперимента и последующего вероятностного анализа полученных результатов мы исходили из предположения о нормальном распределении исходных и выходных показателей. Вместе с тем справедливость сделанных допущений, по крайней мере для выходного показателя NPV , нуждается в проверке.

Для проверки гипотезы о нормальном распределении случайной величины применяются специальные статистические критерии: Колмогорова-Смирнова. В целом MS Excel позволяет быстро и эффективно рассчитать требуемый критерий и провести статистическую оценку гипотез.

Однако в простейшем случае для этих целей можно использовать такие характеристики распределения, как асимметрия (скос) и эксцесс. Для нормального распределения эти характеристики должны быть равны 0. На практике близкими к нулевым значениями можно пренебречь. Смысл коэффициента асимметрии заключается в следующем: в случае положительного значения коэффициента (положительного скоса) самые высокие доходы считаются более вероятными, чем самые низкие. Соответственно в случае отрицательного коэффициента асимметрии более вероятными будут считаться самые низкие доходы.

Экономический смысл эксцесса заключается в следующим: Если две операции имеют симметричные распределения доходов и одинаковые средние, менее рискованной считается инвестиция с большей величиной эксцесса.

Для вычисления коэффициента асимметрии и эксцесса реализованы специальные статистические функции – СКОС() и ЭКСЦЕСС().

Рисунок 15. Заполнение полей диалогового окна Описательная статистика.

Таблица 22. Описательная статистика для исследуемых переменных

	Переменные расходы (V)	Количество (Q)	Цена (P)	Поступления (NCF)	ЧСС (NPV)

Среднее	29,94367	211,633	48,66328	1487,224	3637,75
Стандартная ошибка	0,160212	2,46609	0,246654	25,86201	98,03735
Медиана	30,15143	214,8309	48,98313	1478,252	3603,739
Мода	26,03967	151,54	42,65288	867,0263	1286,712
Стандартное отклонение	3,582452	55,14345	5,515357	578,292	2192,182
Дисперсия выборки	12,83396	3040,8	30,41916	334421,7	4805661
Эксцесс	0,209999	0,209999	0,209999	0,59754	0,59754
Асимметричность	-0,03985	-0,03985	-0,03985	0,450358	0,450358
Интервал	22,834	351,4759	35,15404	3791,825	14374
Минимум	19,29853	47,77592	32,27457	107,9769	-1590,68
Максимум	42,13253	399,2518	67,42861	3899,802	12783,32
Сумма	14971,84	105816,5	24331,64	743612,1	1818875
Счет	500	500	500	500	500
Наибольший(1)	42,13253	399,2518	67,42861	3899,802	12783,32
Наименьший(1)	19,29853	47,77592	32,27457	107,9769	-1590,68
Уровень надежности(95,0%)	0,314773	4,845193	0,484608	50,81178	192,6166

Результатом выполнения указанных действий будет формирование отдельного листа, содержащего вычисленные характеристики описательной статистики для исследуемых переменных. (Таблица 22. Описательная статистика для исследуемых переменных)

Многие из приведенных в данной таблице характеристик нам уже хорошо знакомы, а их значения уже определены с помощью соответствующих функций на листе Результаты анализа. Поэтому рассмотрим лишь те из них, которые не упоминались ранее.

Вторая строка таблицы содержит значения стандартных ошибок e для средних величин распределений. Другими словами, среднее, или ожидаемое, значение случайной величины М(Е) определено с погрешностью .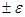

Медиана – это значение случайной величины, которое делит площадь, ограниченную кривой распределения, пополам (т.е. середина численного ряда или интервала). Как и математическое ожидание, медиана является одной из характеристик центра распределения случайной величины. В симметричных распределениях значение медианы должно быть равным или достаточно близким к математическому ожиданию.

Мода – наиболее вероятное значение случайной величины (наиболее часто встречающееся значение в интервале данных). Для симметричных распределений мода равна математическому ожиданию. Иногда мода может отсутствовать.

Эксцесс характеризует остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой. Теоретически эксцесс нормального распределения должен быть равен 0. Однако на практике для генеральных совокупностей больших объемов его малыми значениями можно пренебречь.

Асимметричность (коэффициент асимметрии или скоса –s) характеризует смещение распределения относительно математического ожидания. При положительном значении коэффициента распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания), и наоборот. Для нормального распределения коэффициент асимметрии равен 0. На практике его малыми значениями можно пренебречь. Оставшиеся показатели описательной статистики менее интересны.

Величина Интервал определяется как разность между максимальным и минимальным значениями случайной величины.

Параметры Счет и Сумма представляют собой число значений в заданном интервале и их сумму соответственно.

Последняя характеристика Уровень надежности показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия. По умолчанию уровень надежности принят равным 95%.

Можно указать другой уровень надежности путем ввода соответствующего значения в поле Уровень надежности диалогового окна Описательная статистика. Следует отметить, что чем выше принятый уровень надежности, тем больше величина доверительного интервала для среднего.

Рассчитать доверительный интервал для среднего значения можно также с помощью специальной статистической функции ДОВЕРИТ().

Дополнение Анализ данных содержит целый ряд других полезных инструментов, позволяющих быстро и эффективно осуществить требуемый вид обработки данных.

Имитационное моделирование позволяет учесть максимально возможное число факторов внешней среды для поддержки принятия управленческих решений и является наиболее мощным средством анализа инвестиционных рисков. Необходимость его применения в отечественной финансовой практике обусловлена особенностями российского рынка, характеризующегося субъективизмом, зависимостью от внеэкономических факторов и высокой степенью неопределенности.

Результаты имитации могут быть дополнены вероятностным и статистическим анализом и в целом обеспечивают менеджера наиболее полной информацией о степени влияния ключевых факторов на ожидаемые результаты и возможных сценариях развития событий.

К недостаткам рассмотренного подхода следует отнести:

Трудность понимания и восприятия менеджерами имитационных моделей, учитывающих большое число внешних и внутренних факторов, вследствие их математической сложности и объемности;

При разработке реальных моделей может возникнуть необходимость привлечения специалистов или научных консультантов со стороны;

Относительную неточность полученных результатов по сравнению с другими методами численного анализа и др.

Несмотря на отмеченные недостатки, в настоящее время имитационное моделирование является основой для создания новых перспективных технологий управления и принятия решений в сфере бизнеса, а развитие вычислительной техники и программного обеспечения делает этот метод все более доступным для широкого круга специалистов-практиков.

ЛИТЕРАТУРА

Риск-анализ инвестиционного проекта. Под ред. М,В,Грачевой. – М: Юнити, 2001.

Гультяев . Имитационное моделирование в среде Windows.

Имитационные системы приняти экономических решений, под ред. К.А. Багриновского, Т.И. Конника. – М.: Наука, 1989.

И.Я. Лукасевич. Анализ финансовых операций. – М.: Финансы, 1998.

Н.И. Холод, А.В. Кузнецов, Я.Н. Жихар и др. Экономико-математические методы и модели. – Минск.: БГЭУ, 1999.

О.О. Замков, А.В. Толостопятенко, Ю.Н. Черемных. Математичекие методы в экономике. – М.: ДИС, 1997.

А. Прицкер. Введение в имитационное моделирование и язык СЛАМ. – М.: Мир, 1887.

Статистическое моделирование и прогнозирование, под ред. А.Г. Гринберга. – М.: Финансы и статистика, 1990.

Балабанов и. т. основы финансового менеджмента: учебное пособие. м.:финансы и статистика, 1997.

В.Г. Белолипецкий. Финансы фирмы. - М.: инфра-м, 1998.

В. Беренс, П. Хавранек. Руководство по оценке эффективности инвестиций. - М., 1995.

Абрютина м.с., Грачева..Анализ финансово-экономической деятельности предприятия: :учебно-практическое пособие /абрютина м.с.,грачев а.в. .-м.: изд-во"дело и сервис", 1998 .-256 с.

Бирман Г., Шмидт С. Экономический Анализ Инвестиционных Проектов. - М.: Банки И Биржи, Юнити, 1997.

Бланк И.А.Основы Финансового Менеджмента.Т.1 /Бланк И.А. .-К.: Ника-Центр, 1999 .-592 С.

Экономическая информатика и вычислительная техника : Учебник/ Г.А.Титоренко, Н.И.Черняк, Л.В.Еремин и др.; Под ред. В.П.Косарева, А.Ю.Королева. – Изд. 2-е, перераб. и доп. – М.: Финансы и статистика, 1996.

М. Хэлворсон, М. Янг. Эффективная работа с Microsoft Office 97. СПб: - Питер, 1997.

Р. Персон. Microsoft Excel 97 в подлиннике. СПб: BHV,1997.

А.М. Сидоренко, О.А. Дыкман, А.М. Якушева, Н.В. Сочнева. Компьютерные технологии в финансовом моделировагнии Project Expert5.0. Учебное пособие. Н.Новгород. НКИ, 2001.

А.А.Емельянов, Е.А.Власова, Р.В.Дума. Имитационное моделирование экономических процессов. – М.: Финансы и статистика,2002.

Имитационное моделирование

Курс лекций

Для студентов, обучающихся по специальности

«Прикладная информатика в экономике»

Составитель: Сидоренко А.М, Дыкман О.А., Якушева А.М.

Усова Ю.С

Редактор

Компьютерный набор О.А.Дыкман

Лицензия №

Подписано в печать_______ Формат

Бумага

Уч. – изд___. Усл.-печ.л.

Тираж

Нижегородский коммерческий институт

603140, г. Нижний Новгород. Пр. Ленина, 27

типография НКИ, г. Н.Новгород, пр. Ленина, 25А