Для решения теоретических и практических задач надёжности производственных ЭС и их элементов надо знать законы распределения их отказов. Они получаются посредством обобщения статического материала об отказах. Примем случайную величину (СВ) “Т” за время безотказной работы. За время эксплуатации восстанавливаемых элементов ЭС – «t» величина “Т” принимает “n” значений. Совокупность этих случайных значений величины – статическая выборка объёма “n”. Если значения СВ “Т” расположить в возрастающем (убывающем) порядке и указать относительно каждого как часто оно встречается, то имеем распределение СВ или вариационный ряд на основании которого определяем аналитическую форму неизвестной плотности вероятности f(t) = φ(t) или функцию распределения F(t).

Для построения вариационного ряда диапазон значений СВ “T” разбиваем на интервалы. Подсчитываем количество значений «m» СВ Т, приходящейся на каждый интервал и определяем частоту её попадания в данный интервал:

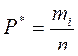                                                                                                (4.77)

где

n – число наблюдений, объём выборки.

Вариационный (статический) ряд

Таблица 4.3

Оптимальная величина интервала:

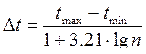                                                                           (4.78)

где

n – число единиц в совокупности (выборке);

(t_max - t_min) – размах вариации СВТ.

Число интервалов :

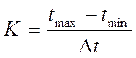                                                                            (4.79)

или проще:

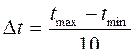                                                                                 (4.80)

Большое значение имеет графический метод изображения вариационного ряда:

§ Полигон распределения (многоугольник): по оси абсцисс откладываем интервалы значений СВ, в их серединах строим ординаты, пропорциональные частотам и концы ординат соединяем.

§ Гистограмма распределения. Над каждым отрезком оси абсцисс, изображающем интервал значений СВ, строится прямоугольник, высота которого пропорциональна частотам интервала.

При уменьшении длинны каждого интервала гистограмма приближается к некоторой плавной кривой, соответствующей плотности распределения величины “T”. Таким образом при построении гистограммы получаем представление о дифференциальном законе распределения СВ Т.

§ Статическая функция распределения F^*(t) – частота событий Т < t в данной выборке:

F^*(t) = p^*(T<t)                                                                          (4.81)

где

t – текущая переменная;

p^* - частота или статическая вероятность события.

F^*(t_i) = n_i/n                                                                                 (4.82)

где

n_i – число отказов, при которых Т < t ;

n – число наблюдений.

Если Т – непрерывная величина, то при увеличении “n” (объёма выборки) F^*(t) – интегральная функция распределения величины Т.

Таким образом, построение статической функции распределения F^*(t) решает вопрос об установлении на основе экспериментальных данных закона распределения СВ.