1. Определим целевую функцию линейной модели:
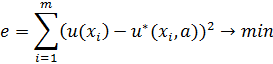
или
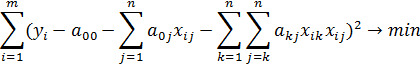
2. Определим систему линейных уравнений
Рассмотрим линейную функцию: u(a,x). Найдем значения a00,....a04 обеспечивающие минимум суммы среднеквадратических ошибок на всех элементах обучающей выборки:
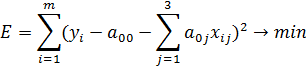
1) Продифференцируем E по переменной a 00
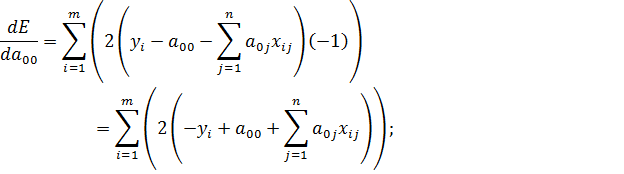
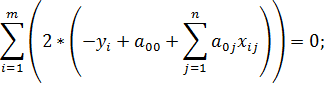
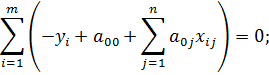
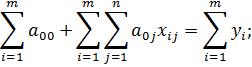
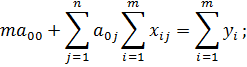
Используя (1), получим первое уравнение системы:
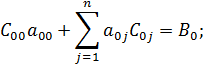
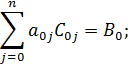
2) Продифференцируем E по переменной a 01
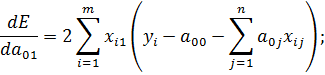
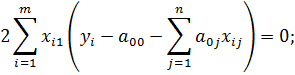
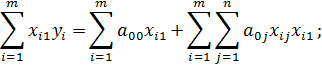
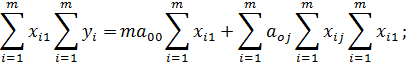
Введем обозначения:
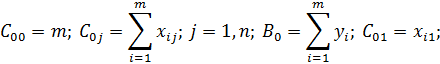
Получим второе уравнение системы:
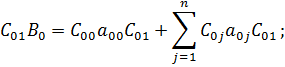
3) Продифференцируем E по переменной a 02
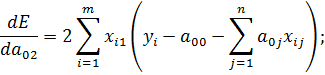
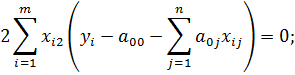
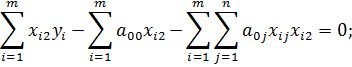
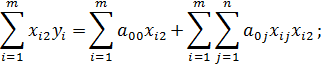
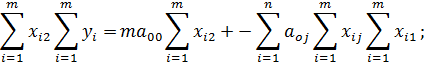
Введем обозначения:
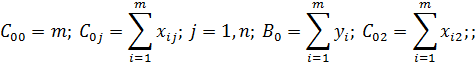
Получим третье уравнение системы:
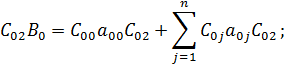
4) Продифференцируем E по переменной a 03
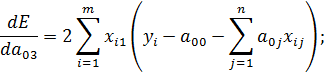
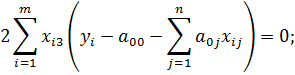
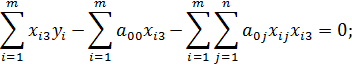
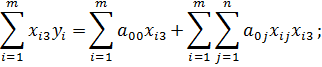
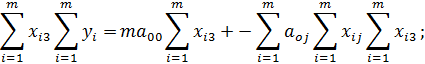
Введем обозначения:
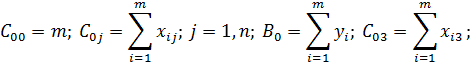
Получим четвертое уравнение системы:
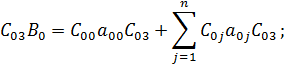
2. Составим систему из 4-х линейных уравнений:
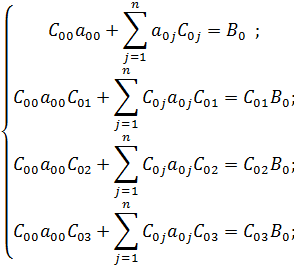
Тогда получаем при n=3:
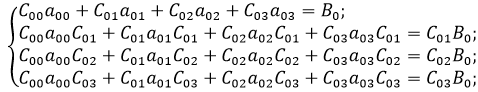
Преобразуем систему при m=32:
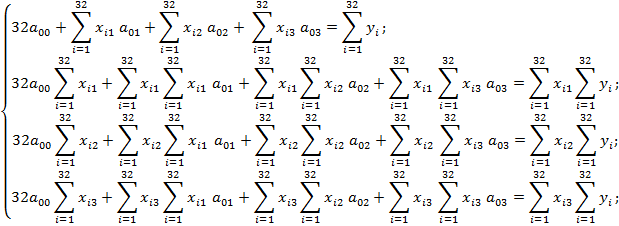
Используя выборку, снова преобразуем систему:
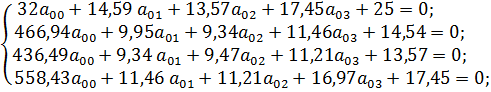
Воспользовавшись методом Гаусса для решения СЛУ, вычислим значения a 00, a 01, a 02, a 03:
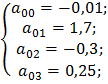
Значения a 00, a 01, a 02, a 03 вставляем в полином первой степени:
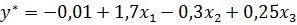
Посчитаем полином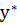 
и найдем ошибку аппроксимации. Результаты представлены в таблице 20. Значение столбца Y** это значение полинома после сравнения с порогом 0,5.
Таблица 20. Значение у* (контролирующая выборка)
| X4 | X5 | X6 | Y | Y* | Y** | |
| 1 | 0,482 | 0,466 | 0,992 | 1 | 0,918 | 1 |
| 2 | 0,431 | 0,408 | 0,996 | 1 | 0,849 | 1 |
| 3 | 0,683 | 0,785 | 1 | 1 | 1,167 | 1 |
| 4 | 0,752 | 1 | 1 | 1 | 1,219 | 1 |
| 5 | 0,689 | 0,894 | 0 | 1 | 0,893 | 1 |
| 6 | 0,810 | 0,773 | 1 | 1 | 1,385 | 1 |
| 7 | 0,505 | 0,276 | 0,203 | 1 | 0,817 | 1 |
| 8 | 0,902 | 0,727 | 1 | 1 | 1,555 | 1 |
| 9 | 0,850 | 0,909 | 1 | 1 | 1,413 | 1 |
| 10 | 0,649 | 0,965 | 0 | 1 | 0,804 | 1 |
| 11 | 0,373 | 0,152 | 0,101 | 1 | 0,604 | 1 |
| 12 | 0,643 | 0,765 | 1 | 1 | 1,104 | 1 |
| 13 | 0,706 | 0,832 | 1 | 1 | 1,191 | 1 |
| 14 | 0,166 | 0,124 | 0,219 | 1 | 0,290 | 0 |
| 15 | 0,333 | 0,130 | 0 | 1 | 0,517 | 1 |
| 16 | 0,413 | 0,176 | 0,239 | 1 | 0,700 | 1 |
| 17 | 0,206 | 0,143 | 0 | 1 | 0,298 | 0 |
| 18 | 0,660 | 0,887 | 0 | 1 | 0,847 | 1 |
| 19 | 0,764 | 0,722 | 1 | 1 | 1,322 | 1 |
| 20 | 0,471 | 0,292 | 0,996 | 1 | 0,952 | 1 |
| 21 | 0,448 | 0,862 | 0 | 1 | 0,493 | 0 |
| 22 | 0,747 | 0,967 | 1 | 1 | 1,219 | 1 |
| 23 | 0,695 | 0,880 | 1 | 1 | 1,157 | 1 |
| 24 | 0,672 | 0,984 | 0,996 | 1 | 1,086 | 1 |
| 25 | 0,568 | 0,961 | 0,996 | 1 | 0,917 | 1 |
| 26 | 0,011 | 0,001 | 0 | 0 | 0,009 | 0 |
| 27 | 0,011 | 0,001 | 0 | 0 | 0,009 | 0 |
| 28 | 0,011 | 0,0006 | 0 | 0 | 0,009 | 0 |
| 29 | 0,0229 | 0,003 | 0 | 0 | 0,028 | 0 |
| 30 | 0,0114 | 0,001 | 0 | 0 | 0,009 | 0 |
| 31 | 0 | 0 | 0 | 0 | -0,01 | 0 |
| 32 | 0 | 0 | 0 | 0 | -0,01 | 0 |
В ходе анализа выявлены три ошибки I-рода и не выявлены ошибки II-рода. Ошибка аппроксимации E вычисляется по формуле:
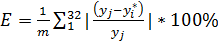= 9,335
Воспользовавшись программой для решения СЛУ, вычислим значения a 00, a 01, a 02, a 03, a 04, a 05, a 06, a 07 a 08, a 09:
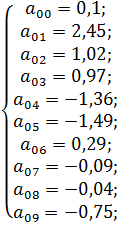
Значения a 00, a 01, a 02, a 03, a 04, a 05, a 06, a 07 a 08, a 09 подставляем в полином второй степени:
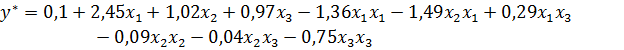
Посчитаем полином 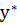и найдем ошибку аппроксимации. Результаты представлены в таблице 21. Значение столбца Y** это значение полинома после сравнения с порогом 0,5.
Таблица 21. Значение у** (контролирующая выборка)
| X4 | X5 | X6 | Y | Y* | Y** | |
| 1 | 0,482 | 0,466 | 0,992 | 1 | 1,431 | 1 |
| 2 | 0,431 | 0,408 | 0,996 | 1 | 1,373 | 1 |
| 3 | 0,683 | 0,785 | 1 | 1 | 1,472 | 1 |
| 4 | 0,752 | 1 | 1 | 1 | 1,380 | 1 |
| 5 | 0,689 | 0,894 | 0 | 1 | 1,064 | 1 |
| 6 | 0,810 | 0,773 | 1 | 1 | 1,417 | 1 |
| 7 | 0,505 | 0,276 | 0,203 | 1 | 1,252 | 1 |
| 8 | 0,902 | 0,727 | 1 | 1 | 1,372 | 1 |
| 9 | 0,850 | 0,909 | 1 | 1 | 1,331 | 1 |
| 10 | 0,649 | 0,965 | 0 | 1 | 1,084 | 1 |
| 11 | 0,373 | 0,152 | 0,101 | 1 | 0,996 | 1 |
| 12 | 0,643 | 0,765 | 1 | 1 | 1,483 | 1 |
| 13 | 0,706 | 0,832 | 1 | 1 | 1,454 | 1 |
| 14 | 0,166 | 0,124 | 0,219 | 1 | 0,751 | 1 |
| 15 | 0,333 | 0,130 | 0 | 1 | 0,832 | 1 |
Таблица 21. Значение у** (контролирующая выборка). Окончание
| X4 | X5 | X6 | Y | Y* | Y** | |
| 16 | 0,413 | 0,176 | 0,239 | 1 | 1,165 | 1 |
| 17 | 0,206 | 0,143 | 0 | 1 | 0,649 | 1 |
| 18 | 0,660 | 0,887 | 0 | 1 | 1,086 | 1 |
| 19 | 0,764 | 0,722 | 1 | 1 | 1,458 | 1 |
| 20 | 0,471 | 0,292 | 0,996 | 1 | 1,384 | 1 |
| 21 | 0,448 | 0,862 | 0 | 1 | 1,162 | 1 |
| 22 | 0,747 | 0,967 | 1 | 1 | 1,395 | 1 |
| 23 | 0,695 | 0,880 | 1 | 1 | 1,448 | 1 |
| 24 | 0,672 | 0,984 | 0,996 | 1 | 1,440 | 1 |
| 25 | 0,568 | 0,961 | 0,996 | 1 | 1,484 | 1 |
| 26 | 0,011 | 0,001 | 0 | 0 | 0,129 | 0 |
| 27 | 0,011 | 0,001 | 0 | 0 | 0,129 | 0 |
| 28 | 0,011 | 0,0006 | 0 | 0 | 0,129 | 0 |
| 29 | 0,022 | 0,003 | 0 | 0 | 0,159 | 0 |
| 30 | 0,011 | 0,001 | 0 | 0 | 0,129 | 0 |
| 31 | 0 | 0 | 0 | 0 | 0,100 | 0 |
| 32 | 0 | 0 | 0 | 0 | 0,100 | 0 |
Ошибка аппроксимации E при обучающей выборке:
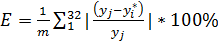=0
В ходе анализа ошибки I и II рода не выявлены.
Таблица 22. Ошибка аппроксимации
| Ошибка аппроксимации на контролирующей выборке | |
| Полином 1 степени | 9,335 |
| Полином 2 степени | 0 |
Полином второй степени допускает меньшее количество ошибок на тестирующей выборке. Полином второй степени в дальнейшем будет использоваться для поиска границы объекта на изображении.
ТЕХНОЛОГИЧЕСКИЙ ПРОЦЕСС ОБРАБОТКИ ДАННЫХ
Технология приобретения знаний
Технологический процесс приобретения знаний представлен на рисунке 4.1.
Рис. 4.1. Технология приобретения знаний
Технология принятия решения
Технологический процесс принятия решений представлен на рисунке 4.2.
Рис. 4.2. Технология принятия решения
ПРОГРАММНЫЕ СРЕДСТВА
Дата: 2018-12-28, просмотров: 408.
