2.1.1. Постановка задачи

На вход системе поступают изображения с выделенными границами грибов. По полученным изображениям необходимо сформировать правила, по которым система будет определять принадлежность пикселя изображения к границе гриба. Правила строятся на основе информационных признаков. Определение множества информационных признаков включает в себя подготовку обучающей и контролирующей выборки для последующего корреляционного анализа. На выходе получим значение, которое будет указывать на принадлежность точки на изображении гриба к границе. Обозначения приведены в таблице 1.

Таблица 1. Обозначения

Обозначение	Название	Диапазон значений переменной
j	Номер признака	1, n
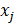
	j признак
	Обучающая выборка
a	Параметры функции u
i	Номер опыта	i = 1,m
ri	Значение коэффициента корреляции
xij	Значение j-го признака в i-ом элементе выборки
О	Множество объектов выборки
С0 ,С1	Классы объектов
е	Целевая функция
Xj	вариация j-го признака

Пусть имеются экспериментально найденные значения случайных величин координат граничных точек и точек, лежащих вне границы X = (x₁, x₂,…x_n)и Y=( y₁,y₂,…y_n).

По следующей формуле находим значения парного коэффициента корреляции.

Таким образом, выявляем зависимость между случайными величинами для выявления наиболее информационных признаков для классификации.

Если коэффициент корреляции принимает значения близкие к 1, то значит, между значениями имеется зависимость (-1 обратная зависимость). Если коэффициент корреляции равен 0, то значит, что значения являются независимыми, но это не является признаком отсутствия или присутствия зависимости.

Классификация представляет собой отнесение объекта к одному из заранее известных классов.

Пусть дано множество объектов О = { o } и n мерное пространство признаков X : X = X ₁ ´ X ₂ ´ … X_n , где X_j – множество значений j–ого признака, j =1, n.

Каждый объект oÎО задан точкой x в n мерном пространстве признаков X : m :  О « X , x = m ( o ), o = m ^-1 ( X ), где x = ( x ₁ , x ₂ ,… x_n ) – вектор значений признаков объекта o , x_ij Î X_j , j = 1, n .

Рассмотрим два класса объектов С₀ и С₁: O = С₀ È С₁, С₀ Ç С₁ = Æ.

Необходимо каждый объект отнести к одному из двух классов С₀ или С₁, т. е. должна быть задана функция

Если известна функция y = u ( x ): 

то k (0) = u ( m ( o )), o Î О.

Необходимо оценить функцию u ( x ) определить ее вид и параметры (а).

Задача определения функции u ( x ) состоит в поиске параметров a функции u *: y * = u *( x , a ), y* Î [0,1], при которой минимизируется значение погрешности для каждого элемента заданной обучающей выборки V = {( x_i , y_i )} , где

y_i = u ( x_i ) – значение функции, полученное в результате проведения i-го опыта( i =1, s ; j =1, n ),

x_i = ( x_{i 1} , x_{i 2} ,… x_in ) – элемент выборки, x_ij – значение j-го признака в i-ом элементе выборки (результата i-го опыта), причем

x_ij Î X_j , где X_j – вариация j-го признака ( i = 1, m , j = 1, n ):

В качестве оценочной функции используется полином второго порядка y *= u *( x , a ):

, где a = (a₀₀, a₀₁, a02, …, a0n, a₁₁, a₁₂, …, a_1n, a₂₂, a₂₃, …, a_nn)

Значение полинома на i-ом элементе обучающей выборки (i=1,m):

Таким образом, мы получаем функцию для оценки значений обучающей выборки.

Окончательная формулировка задачи: необходимо определить множество информационных признаков объекта и значения полинома, найти параметры a функции u *, при которой минимизируется значение погрешности для каждого элемента заданной обучающей выборки V .

2.2. Использование системы для определения границ изображения.

2.2.1. Постановка задачи

На основе полинома второго порядка, определенного ранее, необходимо построить характеристическую функцию g₁(x_i, a), определяющую принятие решение об отнесении пикселя изображения к фону или грибу. Таблица 2 содержит список обозначений.

Таблица 2. Обозначения

Обозначение	Название	Диапазон значений переменной
	Характеристическая функция	[0;1]
	Полином
	i признак
i	Номер признака	1, n
	Параметр
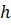
	Порог принятия решений	0-1
	Функция	[0;1]

На основе полученного полинома

формируем принятие решения об отнесении объекта к классу.

Для этого строим характеристическую функцию g ₀ ( x_i , a ), определяющую принятие решения об отнесении объекта o_i ( o_i = m ^-1 ( x_i )) к классу C ₀:

Аналогично строится характеристическая функция g ₁ ( x_i , a ), определяющая принятие решения об отнесении объекта o_i ( o_i = m ^-1 ( x_i )) к классу C ₁:

h может быть равен 0,5, но на практике его значения подбираются для того, чтобы количество ошибочных решений было минимальным.

Ошибки первого и второго рода:

1. ;

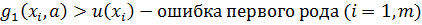2. .

Окончательная формулировка задачи: необходимо подобрать такой h, при котором минимизируются ошибки I и II рода.