Контроль значений признаков и восстановление ошибочных данных
⇐ ПредыдущаяСтр 8 из 10Следующая ⇒
Поможем в ✍️ написании учебной работы
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

 

Для контроля данных найдем:

1. Минимальные и максимальные значения каждого признака в выборке.

2. Оценки математического ожидания значений признаков.

3. Оценку среднего квадратичного отклонения.

4. Стандартные ошибка среднего.

5. Отношение стандартной ошибки среднего к среднему значению.

Результаты представлены в таблице 14.

Таблица 14. Значения признаков

  X1 X2 X3 X4 X5 X6 X7 X8 X9
Мин 0080 0000 0080 0000 0000 0000 0000 0000 0000
Макс 0255 3359 0255 0174 15596 0255 0065 6425 0033
Сред 0216 0710 0222 0080 7232 0132 0017 0643 0006
Откл 37,35 669,48 45,551 53,775 5765,7 123,8879 15,716 1512,7 7,36114
СОШ 4,669 83,685 5,6939 6,72188 720,71 15,48599 1,96461 189,08 0,92014
ОСО 0,021 0,1178 0,0257 0,0844 0,099 0,117 0,116 0,293 0,1517

 

 

Для решения вопроса о «выскакивающих» (ошибочных) значениях необходимо найти диапазон значений фактора [ aj , bj ] ( j =1, M + K ), в котором должно находиться 95% значений фактора выборки:

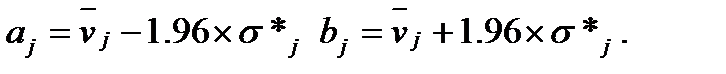
Далее необходимо найти процент значений рассматриваемого фактора непопадающих в этот диапазон. Если таких значений меньше 5%, то считается, что «выскакивающих» значений нет. В противном случае необходимо удалить одно из «выскакивающих» значений (значение наиболее удаленное от оценки среднего) и вновь воспользоваться этой же методикой.

В таблице 15 приведен процент попадающих в диапазон значений фактора [ aj , bj ].

Таблица 15. Диапазон значений

Х1 Х2 Х3 X4 X6 X6 X7  X8 X9
95,3125 95,3125 95,3125 100 100 100 95,3125 95,3125 95,3125

Нормирование значений признаков

 

Нормирование значений - процесс преобразования значений, при котором не изменяется размерность выборки. Нормировать значения факторов необходимо для приведения значений факторов к одному сегменту вариаций значений. Нормализованная выборка приведена в таблице 16.

 

Таблица 16. Нормализованная выборка

  X1 X2 X3 X4 X5 X6 X7 X8 X9 Y
1 0,817 0,184 0,914 0,672 0,561 0,000 0,185 0,012 0,182 1
2 0,749 0,176 0,920 0,483 0,466 0,992 0,308 0,048 0,121 1
3 0,720 0,177 0,897 0,259 0,140 0,996 0,446 0,106 0,333 1
4 0,851 0,170 0,937 0,431 0,409 0,996 0,369 0,079 0,212 1
5 0,800 0,245 0,663 0,598 0,582 0,996 0,415 0,070 0,242 1
6 0,669 0,311 0,851 0,684 0,785 1,000 0,338 0,045 0,121 1
7 0,394 0,316 0,309 0,753 0,748 1,000 0,308 0,053 0,030 1
8 0,623 0,227 0,606 0,753 1,000 1,000 0,200 0,022 0,030 1
9 0,720 0,196 0,937 0,851 0,815 1,000 0,108 0,013 0,030 1
10 0,771 0,208 0,937 0,690 0,895 0,000 0,185 0,024 0,091 1
11 0,800 0,279 0,977 0,684 0,476 1,000 0,231 0,012 0,212 1
12 0,783 0,280 0,657 0,810 0,774 1,000 0,292 0,048 0,121 1
13 0,640 0,581 0,377 0,782 0,724 1,000 0,477 0,106 0,333 1
14 0,509 0,503 0,611 0,506 0,276 0,204 0,338 0,078 0,212 1
15 0,840 0,204 0,983 0,920 0,692 1,000 0,431 0,071 0,242 1
16 0,926 0,172 1,000 0,902 0,727 1,000 0,338 0,045 0,212 1
17 0,943 0,115 0,994 1,000 0,680 1,000 0,338 0,053 0,091 1
18 0,897 0,249 0,994 0,851 0,909 1,000 0,215 0,022 0,091 1
19 0,794 0,308 0,994 0,828 0,864 1,000 0,123 0,013 0,030 1
20 0,726 0,404 0,486 0,649 0,965 0,000 0,185 0,024 0,091 1
21 0,749 0,118 0,709 0,506 0,328 0,122 0,123 0,010 0,061 1
22 0,846 0,167 0,937 0,374 0,153 0,102 0,200 0,024 0,182 1
23 0,754 0,252 0,949 0,224 0,029 0,196 0,292 0,054 0,061 1
24 0,737 0,061 0,703 0,644 0,766 1,000 0,292 0,025 0,121 1
25 0,629 0,085 0,509 0,782 0,806 1,000 0,108 0,010 0,121 1
26 0,874 0,192 0,966 0,707 0,833 1,000 0,138 0,018 0,030 1
27 0,800 0,167 0,709 0,511 0,398 1,000 0,231 0,015 0,758 1
28 0,920 0,162 0,954 0,167 0,124 0,220 0,062 0,003 0,061 1
29 0,800 0,271 0,949 0,172 0,273 0,961 0,200 0,013 0,182 1
30 0,777 0,296 0,937 0,333 0,130 0,000 0,031 0,001 0,061 1
31 0,874 0,102 0,989 0,534 0,138 0,192 0,323 0,018 0,879 1
32 0,909 0,092 0,874 0,414 0,176 0,239 0,292 0,024 0,212 1
33 0,914 0,157 0,994 0,207 0,123 0,000 0,077 0,013 0,030 1
34 0,811 0,216 0,697 0,207 0,144 0,000 0,308 0,015 0,545 1
35 0,886 0,174 0,994 0,190 0,085 0,000 0,215 0,007 0,394 1
36 0,954 0,153 0,994 0,661 0,888 0,000 0,277 0,016 0,515 1
37 0,960 0,049 1,000 0,730 0,860 0,000 0,277 0,024 0,697 1
38 0,920 0,121 0,891 0,764 0,723 1,000 0,338 0,016 0,758 1
39 0,863 0,186 0,794 0,609 0,550 0,996 0,323 0,018 1,000 1
40 0,766 0,182 0,737 0,471 0,293 0,996 0,138 0,006 0,242 1
41 0,137 1,000 0,023 0,713 0,865 1,000 1,000 1,000 0,333 1
42 0,131 0,909 0,029 0,448 0,863 0,000 0,954 0,934 0,121 1
43 0,000 0,045 0,000 0,632 0,974 0,996 0,154 0,128 0,121 1
44 0,777 0,606 0,989 0,747 0,967 1,000 0,785 0,792 0,152 1
45 0,760 0,549 0,983 0,207 0,283 0,000 1,000 0,913 0,061 1
46 0,423 0,382 0,337 0,695 0,881 1,000 0,923 0,795 0,212 1
47 0,669 0,544 0,966 0,420 0,638 1,000 0,354 0,162 0,030 1

Таблица 16. Нормализованная выборка. Окончание

  X1 X2 X3 X4 X5 X6 X7 X8 X9 Y
48 0,554 0,239 0,474 0,672 0,985 0,996 0,338 0,111 0,212 1
49 0,491 0,093 0,486 0,759 0,940 0,996 0,431 0,153 0,061 1
50 0,566 0,201 0,531 0,569 0,961 0,996 0,338 0,144 0,061 1
51 0,931 0,030 0,931 0,000 0,000 0,000 0,092 0,000 0,182 0
52 0,937 0,000 0,937 0,011 0,001 0,000 0,015 0,000 0,061 0
53 0,943 0,000 0,943 0,000 0,000 0,000 0,000 0,000 0,000 0
54 0,869 0,033 0,880 0,011 0,001 0,000 0,031 0,000 0,121 0
55 0,994 0,107 1,000 0,011 0,002 0,000 0,015 0,000 0,030 0
56 1,000 0,000 1,000 0,011 0,001 0,000 0,015 0,000 0,061 0
57 1,000 0,000 1,000 0,000 0,000 0,000 0,015 0,000 0,000 0
58 0,971 0,149 0,977 0,023 0,003 0,000 0,000 0,000 0,000 0
59 1,000 0,000 1,000 0,011 0,001 0,000 0,000 0,000 0,000 0
60 1,000 0,000 1,000 0,011 0,001 0,000 0,000 0,000 0,000 0
61 1,000 0,000 1,000 0,011 0,002 0,000 0,000 0,000 0,000 0
62 1,000 0,000 1,000 0,000 0,000 0,000 0,000 0,000 0,000 0
63 1,000 0,000 1,000 0,017 0,003 0,000 0,000 0,000 0,000 0
64 0,971 0,131 0,960 0,000 0,000 0,000 0,000 0,000 0,000 0

 

Выбор информационных признаков

 

Один из методов выделения информационных признаков – подсчет коэффициентов корреляции между факторами и показателем.

Информативность фактора определяется путем сравнения абсолютной величины коэффициента корреляции с пороговым значением:

,

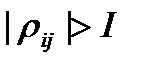где I – задаваемое пороговое значение.

Коэффициент корреляции определяется по формуле:

,

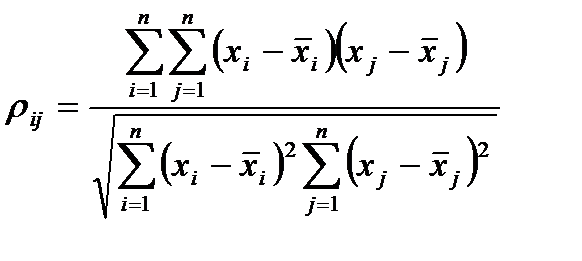 где 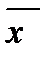- оценка первичных моментов .

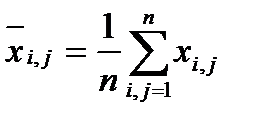При нахождении коэффициентов корреляции необходимо использовать нормированные значения факторов. Пороговым значением I является значение 0,56.

Таблица 17. Коэффициенты корреляций признаков

  X1 X2 X3 X4 X5 X6 X7 X8 X9 Y
X1 1                  
X2 -0,625 1                
X3 0,902 -0,514 1              
X4 -0,426 0,359 -0,350 1            
X5 -0,572 0,438 -0,510 0,889 1          
X6 -0,418 0,263 -0,330 0,710 0,656 1        
X7 -0,586 0,780 -0,488 0,441 0,492 0,370 1      
X8 -0,565 0,765 -0,470 0,159 0,315 0,128 0,877 1    
X9 0,020 0,046 -0,052 0,266 0,124 0,153 0,257 -0,007 1  
Y -0,484 0,479 -0,336 0,774 0,667 0,569 0,540 0,226 0,361 1

 

По результатам корреляционного анализа выбраны три наиболее информативных признака X4, X5, X6. Данные признаки выделены в таблице 17 цветом.

 

Дата: 2018-12-28, просмотров: 443.

⇐ Предыдущая12345678910Следующая ⇒
fb
inst
tw
vk
Материалы представленные на сайте исключительно с целью ознакомления пользователям Интернета и не преследуют коммерческих целей или нарушение авторских прав. © 2018 - 2024