воздушных и кабельных линий

Ток нулевой последовательности ВЛЭП возвращается через землю и по заземленным цепям, расположенным параллельно линии (защитные тросы, рельсовые пути вдоль линии и др.). Главная трудность точного определения сопротивления нулевой последовательности ВЛЭП связана с учетом распределения тока в земле. Достаточно полное и строгое решение в предположении постоянства электрической проводимости земли выполнено Карсоном. Установленные им формулы позволяют вычислить отдельные составляющие и полное сопротивление нулевой последовательности ВЛЭП при токах промышленной частоты и обычно встречающихся значениях проводимости земли.

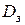Представим себе однопроводную линию переменного тока, обратным проводом которой служит земля (рис 9.8). Плотность тока в земле распределена по мере удаления от линии. Наибольшая плотность тока имеет место на поверхности земли непосредственно под проводником. Индуктивность такой линии может быть определена как индуктивность эквивалентной двухпроводной линии с расстоянием между проводами , которое называется эквивалентной глубиной возврата тока через землю и может

быть определено как

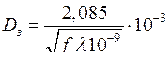, м,                                 (9.25)

где f – частота тока, Гц; λ – удельная проводимость земли, .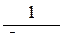

При частоте 50 Гц и среднем значении 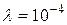 величина 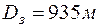. При отсутствии данных о проводимости земли обычно принимают .

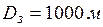Таким образом, индуктивное сопротивление линии находится как

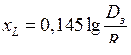.                                      (9.26)

Здесь 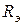 − эквивалентный радиус провода. Для линии с расщепленными проводами вместо  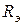следует вводить средний геометрический радиус  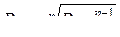системы проводов одной фазы, где n – число проводов в фазе, а_ср – среднее геометрическое расстояние между проводами одной фазы.

Активное сопротивление линии складывается из активного сопротивления провода 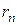 и дополнительного сопротивления 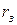, учитывающего потерю активной мощности в земле от протекающего в ней тока. Сопротивление  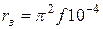практически не зависит от проводимости земли.

Сопротивление, обусловленное взаимоиндукцией между параллельными линиями с расстоянием 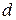 между осями их проводов, определятся как

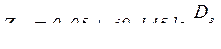.                           (9.27)

Для трехфазной одноцепной линии сопротивление взаимоиндукции между фазами при возврате тока через землю определяется как

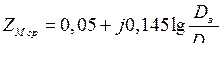                             ,                            (9.28)

где 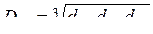 − среднее расстояние между проводами.

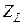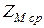Зная  и , можно найти сопротивление нулевой последовательности одноцепной трехфазной линии. Оно численно равно эффективному значению напряжения, которое должно быть приложено к каждому проводу данной линии, чтобы покрыть падение напряжения при протекании в фазах токов нулевой последовательности, т.е.

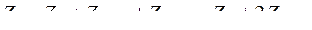.                   (9.29)

После несложных преобразований получим:

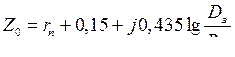.                                (9.30)

Если по линии протекает ток прямой последовательности, то:

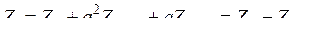.                  (9.31)

После подстановки и преобразования получим:

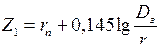.                                       (9.32)

В то время как при токе прямой (или обратной) последовательности взаимоиндукция с другими фазами уменьшает сопротивление фазы, при токе нулевой последовательности она, напротив, увеличивает его. Поскольку 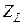 и 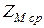 у линии соизмеримы, величины  и 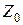 резко различаются между собой.

Сопротивление нулевой последовательности каждой цепи двухцепной линии дополнительно увеличивается благодаря взаимоиндукции с проводами параллельной цепи. Сопротивление взаимоиндукции между проводом одной цепи и тремя проводами другой цепи можно определить по (9.28), где обе составляющие должны быть увеличены в 3 раза. Вместо 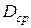 введено среднее геометрическое расстояние  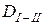между цепями, определяемое через расстояние от каждого провода (a , b , c) цепи I до каждого провода (a ’, b ’, c ’) цепи II:

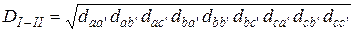.           (9.33)

Тогда искомое сопротивление:

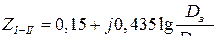.                             (9.34)

В случае, если параллельные цепи одинаковые, т.е. 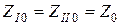, то сопротивление нулевой последовательности каждой из них будет:

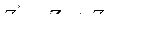.                                       (9.35)

Сопротивление на фазу двухцепной линии будет определяться как

.                        (9.36)

Увеличение сопротивления нулевой последовательности вследствие влияния взаимоиндукции параллельной цепи не превышает 10 % при расстояниях между цепями порядка 400–500 м. При расположении обеих цепей на одной опоре взаимоиндукция проявляется особенно сильно.

Теперь оценим влияния тросов на величину сопротивления нулевой последовательности линии. Тросы используют в качестве средства грозозащиты линии, располагая их в верхней точке опоры. До последнего времени тросы заземляли практически на каждой опоре (рис. 9.4а).

                                   а)                                                                   б)

Рис. 9.4. Влияние тросов

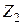При этом в образующихся короткозамкнутых контурах возможно протекание наведенных токов. Они малы при протекании по линии симметричной системы токов, следовательно,  и  практически не зависят от наличия заземленных тросов и могут быть значительными при протекании по линии тока нулевой последовательности. При этом ответная реакция от наведенных токов в тросе может существенно уменьшить сопротивление нулевой последовательности линии.

В последнее время для линий большой протяженности стали применять другую систему заземления защитных тросов. Тросы подвешивают на изоляторах и разрезают на ряд участков (рис. 9.4б). С одного конца каждого участка тросы заземляют, а с другого между тросом и землей оставляют искровой промежуток, пробой которого наступает при возникновении перенапряжения определенной величину. При такой системе заземления тросов они практически не сказываются на сопротивлении нулевой последовательности линии.   

При нескольких заземленных тросах их влияние на сопротивление нулевой последовательности сказывается сильнее.

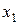 В приближенных расчетах в качестве средних соотношений между индуктивными сопротивлениями  и  для воздушных линий можно принимать значения, приведенные в таблице 9.4.

                                                                                 Таблица 9.4

Средние значения соотношений между  и 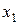для воздушных линий передачи

Характеристика линии	отношение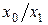
Одноцепная линия без тросов	3,5
Одноцепная линия со стальными тросами	3,0
Одноцепная линия с хорошо проводящими тросами	2,0
Двухцепная линия без тросов	5,5
Двухцепная линия со стальными тросами	4,7
Двухцепная линия с хорошо проводящими тросами	3,0

Реактивное емкостное сопротивление воздушной линии (на 1 км) определяется по следующим выражениям:

− для прямой (обратной) последовательности без учета влияния земли оно оказывается незначительным

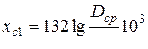,                                     (9.37)

где 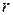 − радиус провода;

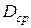   − среднее геометрическое расстояние между проводами фаз;

− для нулевой последовательности

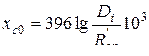,                                     (9.38)

где 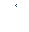 − средний геометрический радиус систем трех проводов линии;

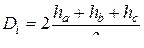   − среднее расстояние проводов фаз до их зеркальных отражений относительно поверхности земл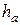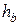и ( ,  и 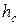 − высоты подвеса проводов фаз относительно земли). Заземленный трос несколько снижает емкостное сопротивление и заметно это лишь в нулевой последовательности.

Кабельные линии. Активное и индуктивное сопротивления нулевой последовательности кабеля можно определить так же, как и для ВЛЭП, используя (9.30). Прокладку кабеля производят на относительно малой глубине. Поэтому распределение тока практически не отличается от ВЛЭП. Это позволяет при определении сопротивления нулевой последовательности кабеля исходить из тех же принципов, что и для ВЛЭП.

Если бы трехжильный кабель не обладал проводящей оболочкой, то его сопротивление 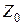 можно определить по (9.30), вводя в выражение среднегеометрический радиус трех жил .

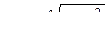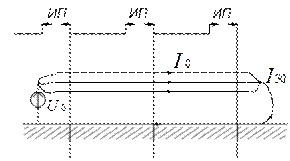
Оболочка кабеля, как правило, заземлена на концах и в промежуточных точках (муфтах), поэтому она образует путь для токов нулевой последовательности, параллельный земле (рис. 9.12). В этом отношении оболочка кабеля аналогична заземленным тросам у ВЛЭП. На распределение тока между оболочкой и землей существенное влияние оказывает не только собственное сопротивление оболочки, но и сопротивление ее заземлений, величины которых зависят от характера прокладки кабеля (траншея, блоки, эстакады и т.д.) и ряда других факторов, что очень затрудняет расчет сопротивления нулевой последовательности кабеля.

В приближенных расчета для трехжильного кабеля принимают:

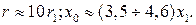                              (9.39)

Единственный путь получения надежных данных о Z₀ кабеля состоит в проведении соответствующих замеров в реальных условиях.

Для трехжильного кабеля с круглыми жилами реактивное емкостное сопротивление нулевой последовательности можно найти по выражению:

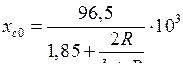                            ,                                 (9.40)

где 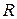 − радиус жилы;

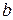 и 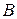 − толщина фазной и поясной изоляции.

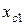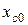Для кабеля с секторными жилами, имеющими ту же поверхность проводника и ту же толщину изоляции, как и у кабеля с круглыми жилами, емкостные сопротивления  и  несколько меньше.