Мгновенные значения фазных величин трехфазной системы можно получить, как проекции трех фазных величин на одну ось времени, так и проектируя один вектор на три оси времени, сдвинутых на 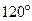 . Этот вектор носит название обобщенного или изображающего вектора (рис. 8.3).
. Этот вектор носит название обобщенного или изображающего вектора (рис. 8.3).
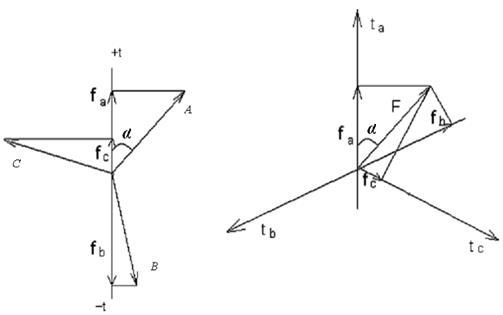
Рис. 8.3. Обобщенный вектор трехфазной системы
Связь между двумя системами определяется соотношениями:

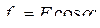
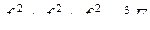
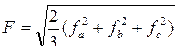
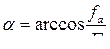
Обобщенный вектор удобно представить в неподвижной декартовой системе координат xy. Такой способ носит название замены переменных. Число переменных при замене не изменяется. Связь между системами определяется соотношениями:
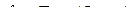
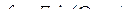
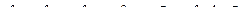
В симметричном режиме:

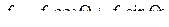
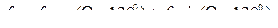
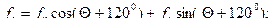
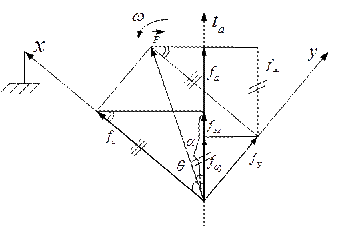
Рис. 8.4. Замена переменных
В несимметричном режиме машины вводится нулевая составляющая  . При этом
. При этом 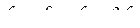 .
.


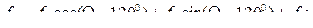 (8.3)
(8.3)
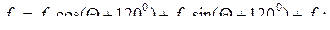
 − частный случай. Симметричный режим машины.
− частный случай. Симметричный режим машины.
В декартовой системе координат (двухфазной машине) число коэффициентов собственных и взаимных индуктивностей уменьшилось, но не устранена переменность коэффициентов. Такая система координат осей х, у, неподвижных в пространстве, используется при анализе переходных процессов в несимметричных режимах синхронных машин. При анализе переходных процессов асинхронных машин вводятся оси, связанные с ротором при переменной скорости вращения. Такие оси носят название осей α, β.
Симметричные переходные процессы в синхронной машине целесообразно исследовать в системе координат, вращающихся вместе с ротором (ось х при этом совмещают с осью d ротора). Эта система осей называется осями d , q. Удобство системы координат, жестко связанных с ротором, для синхронной машины заключается в том, что для наблюдателя, вращающегося вместе с этими осями, машина в магнитном отношении оказывается симметричной независимо от положения ротора. То есть ротор вращается вместе со статором и ротор относительно статора остается неподвижным. В такой модельной машине невозможно образование ЭДС вращения, но они могут быть получены при обратном переходе от двухфазной машины к трехфазной.
Поэтому в системе координат d , q , потокосцепления уже не содержат переменных индуктивностей, а дифференциальные уравнения имеют постоянные коэффициенты, что существенно облегчает исследование. Преобразование к осям
d , q является практически единственным, приводящим дифференциальные уравнения синхронной машины с периодическими коэффициентами к уравнениям с постоянными коэффициентами. Это делает преобразование к осям d , q весьма важным, играющим фундаментальное значение в теории синхронной машины. Это преобразование было предложено Блонделем для установившегося режима и развито для переходных процессов Парком и Горевым. Уравнения носят название уравнений по огибающим (так как в новой системе координат и старой системе координат максимальные значения совпадают) или уравнений Парка−Горева.
Модель преобразованной машины представлена на рисунке 8.5. Если для этой
машины составить дифференциальные уравнения, то это будут дифференциальные уравнения с постоянными коэфицентами, которые можно будет решить и осуществить обратный переход к трехфазной машине по соотношениям (8.3).
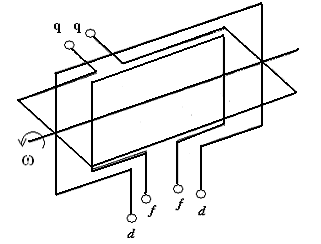
Рис. 8.5. Модель преобразованной синхронной машины
Потокосцепления модели и связь параметров модели и трехфазной машины:

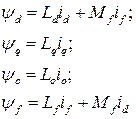
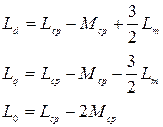 (8.4)
(8.4)
8.4. Вывод уравнений Парка−Горева
Заменим 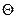 на
на  при этом
при этом 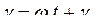 и выразим все входящие в уравнение (8.1) переменные через новые переменные по соотношениям (8.3):
и выразим все входящие в уравнение (8.1) переменные через новые переменные по соотношениям (8.3):


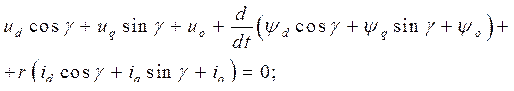
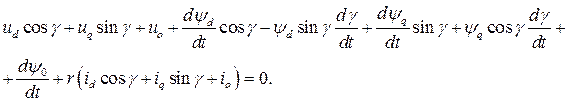
Группируем слагаемые:
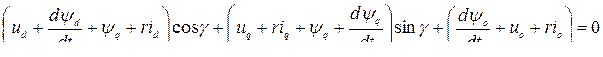 .
.
Приравнивая нулю каждого выражения в скобках и добавляя уравнение для обмотки возбуждения (8.1) и соотношения для потокосцеплений (8.4), получаем дифференциальные уравнения модели, носящие название уравнений Парка−Горева, выражающие основу теории двух реакций:

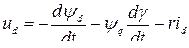
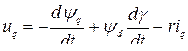
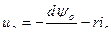
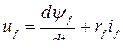 (8.5)
(8.5)
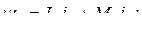
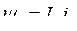
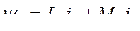
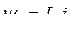
Некоторые допущения, которые имели место, могут быть сняты. Так, если добавить уравнение движения, то уравнения могут быть использованы для решения задач расчета электромеханических переходных процессов.
Например: 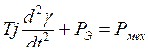 .
.
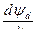 − ЭДС трансформации. С учетом известного выражения для ЭДС вращения
− ЭДС трансформации. С учетом известного выражения для ЭДС вращения  при синхронной скорости вращения
при синхронной скорости вращения 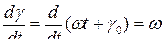 и
и 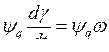 − ЭДС вращения; ri − падение напряжения на активном сопротивлении.
− ЭДС вращения; ri − падение напряжения на активном сопротивлении.
8.5. Уравнения Парка−Горева в системе относительных единиц
При 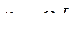 и синхронной скорости
и синхронной скорости 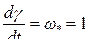 . В дальнейшем опускаем индекс относительной величины *, и уравнения (8.5) принимают вид:
. В дальнейшем опускаем индекс относительной величины *, и уравнения (8.5) принимают вид:


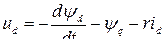

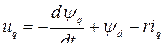
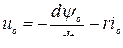
 (8.6)
(8.6)
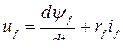
 .
.
В такой форме уравнения применяются для анализа электромагнитных переходных процессов.
8.6. Уравнения Парка−Горева в операторной форме
Решение уравнений Парка−Горева обычно производят в операторной форме с применением преобразования Лапласа. При этом уравнения становятся алгебраическими и решаются стандартными методами. Для упрощения решения его производят при нулевых начальных условиях, то есть для приращений. По принципу наложения полученные решения для приращений суммируются с начальными условиями. С учетом основных соотношений преобразований Лапласа: 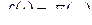 и
и 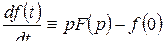 .
.

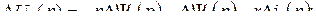
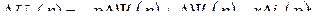
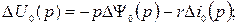
 (8.7)
(8.7)
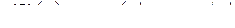

 .
.
Из выражений (8.7) могут быть определены операторные реактивности синхронной машины:
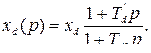
Здесь: 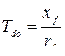 =
= 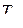 − постоянная времени обмотки возбуждения при разомкнутом статоре;
− постоянная времени обмотки возбуждения при разомкнутом статоре; 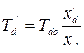 − постоянная времени обмотки возбуждения при короткозамкнутом статоре. В начальный момент времени −
− постоянная времени обмотки возбуждения при короткозамкнутом статоре. В начальный момент времени − 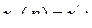 в установившемся режиме −
в установившемся режиме − 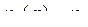 .
.
Дата: 2019-02-02, просмотров: 442.