Выражения для токов и напряжений в месте несимметричного короткого замыкания приведены в таблице 10.1.
Таблица 10.1
Токи и напряжения при различных видах КЗ
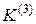
| 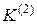
| 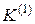
| 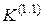
| |
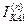
| 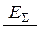
| 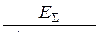
| 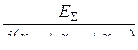
| 
|
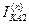
| 0 | 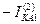
| 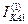
| 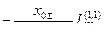
|
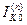
| 0 | 0 | 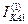
| 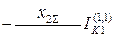
|
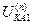
| 0 | 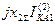
| 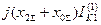
| 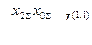
|
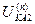
| 0 | 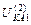
| 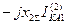
| 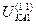
|
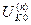
| 0 | − | − 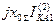
| 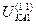
|
Таким образом, обобщая данные таблицы 10.1, можно получить формулы:
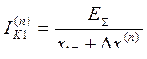 ; (10.37)
; (10.37)
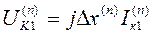 . (10.38)
. (10.38)
На основании анализа таблицы 10.1 и выражения 10.37 можно сформулировать правило эквивалентности прямой последовательности: Ток прямой последовательности любого несимметричного КЗ может быть определен как ток симметричного трехфазного КЗ, удаленного от точки действительного КЗ на дополнительное сопротивление, не зависящее от параметров схемы замещения прямой последовательности и определяемое результирующими сопротивлениями обратной и нулевой последовательности относительно точки КЗ.
При расчетах всех видов несимметричных коротких замыканий, в соответствии с правилом эквивалентности прямой последовательности, достаточно определить лишь прямую последовательность тока 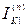 . Все остальные расчетные величины выражаются через
. Все остальные расчетные величины выражаются через 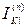 и даны в таблице 10.1.
и даны в таблице 10.1.
Для определения тока прямой последовательности требуется предварительно найти результирующие реактивности схем обратной и нулевой последовательностей и дополнительные реактивности, зависящие от вида КЗ ( 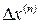 ), которые определяются по таблице 10.2.
), которые определяются по таблице 10.2.
Модуль полного тока в месте КЗ определяется как
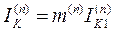 , (10.39)
, (10.39)
где  – коэффициент, зависящий от вида КЗ (табл. 10.2).
– коэффициент, зависящий от вида КЗ (табл. 10.2).
Таблица 10.2
Расчетные соотношения дополнительной реактивности 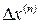 и
и
коэффициента 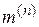 , зависящих от вида КЗ
, зависящих от вида КЗ
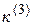
| 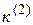
| 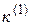
| 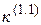
| |
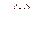
| 0 | 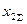
| 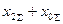
| 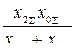
|
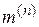
| 1 | 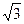
| 3 | 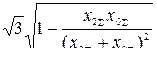
|
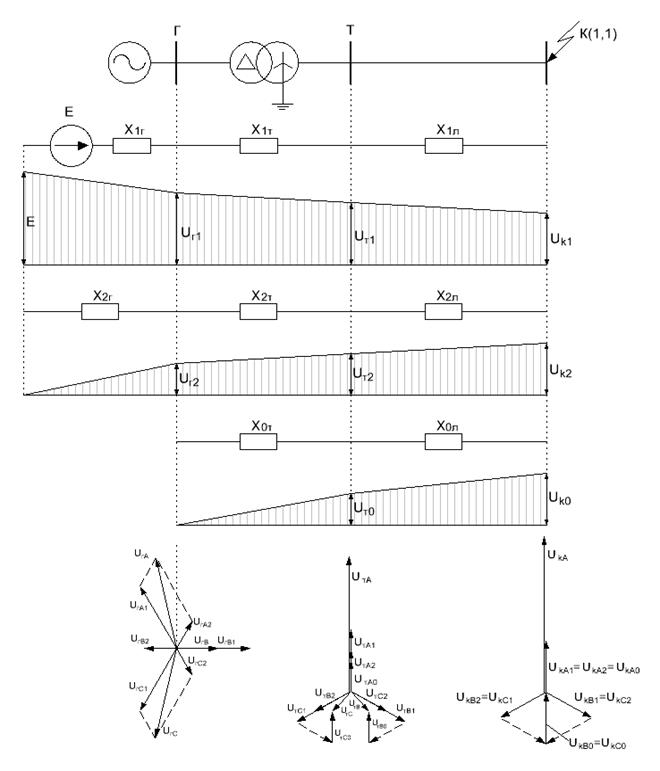
Полученные соотношения справедливы для точки КЗ. По мере удаления от точки КЗ напряжение прямой последовательности увеличивается, а напряжения обратной и нулевой последовательностей уменьшаются. Это иллюстрируется эпюрами распределения напряжений отдельных последовательностей для простейшей схемы при 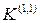 (рис. 10.8). Там же даны векторные диаграммы напряжений. Видно, что по мере удаления от точки КЗ симметрия трехфазной системы восстанавливается.
(рис. 10.8). Там же даны векторные диаграммы напряжений. Видно, что по мере удаления от точки КЗ симметрия трехфазной системы восстанавливается.
а) б) в)
Рис. 10.8. Распределение напряжений в сети при 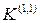 и векторные диаграммы напряжений:
и векторные диаграммы напряжений:
а – на шинах генератора; б – на стороне ВН трансформатора; в – в месте КЗ
Комплексные схемы замещения
Установленные в предыдущих параграфах соотношения между симметричными составляющими напряжений в месте короткого замыкания позволяют для каждого вида несимметричного КЗ соединить схемы отдельных последовательностей и образовать комплексную схему замещения для соответствующего вида КЗ.
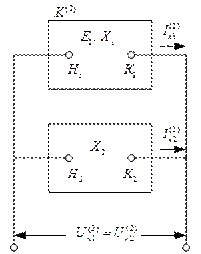
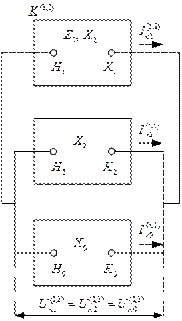
Такие схемы приведены на рисунке 10.9

а) б) в)
Рис. 10.9. Комплексные схемы замещения
а – для однофазного КЗ на землю; б – для двухфазного КЗ;
в – для двухфазного КЗ на землю
Применение комплексных схем замещения удобно при физическом и математическом моделировании. Они позволяют моделирование КЗ любого вида и в любой точке расчетной схемы. При этом могут быть определены симметричные составляющие токов в любой ветви схемы и симметричные составляющие напряжений в любом узле. По полученным значениям симметричных составляющих могут быть синтезированы полные величины токов и напряжений.
Пример составления комплексной схемы замещения при однофазном КЗ для схемы рисунка 10.10 приведен на рисунке 10.11.


Рис. 10.10. Схема электропередачи

Рис. 10.11. Комплексная схема замещения при 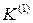
Дата: 2019-02-02, просмотров: 368.