на постоянное напряжение

Простейшим случаем решения уравнений Парка−Горева является исследование переходного процесса при включении обмотки возбуждения на постоянное напряжение. Решение этой задачи имеет большое значение при анализе систем регулирования и форсировки возбуждения, так как выявляет факторы, влияющие на скорость изменения тока возбуждения и скорость изменения ЭДС статора.

Допущения:

1) все начальные условия нулевые ;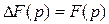

2) режим симметричный ;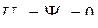

3) постоянное напряжение возбуждения, т.е. нет АРВ ;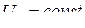

4) статор разомкнут, т.е. токов статора не будет. .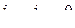

Рис. 8.6. Расчетная модель

С учетом начальных условий уравнения (8.7) принимают вид:

                                                                            (8.8)

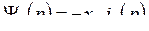
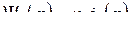
С подстановкой потокосцеплени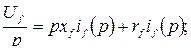й

;  ;                                                     

 и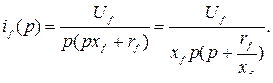

Решение уравнения с учетом табличного соотношения перехода к временной функции :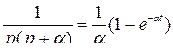                                    

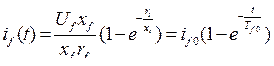− закон изменения тока возбуждения. 

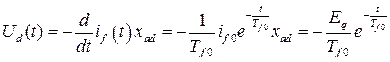 − огибающая ЭДС трансформации;  

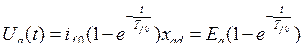− огибающая ЭДС вращения.

С учетом (8.3) , 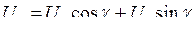− при переходе к трехфазной машине:

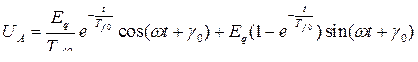.                                 (8.9)

Здесь: 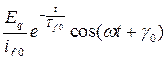 − ЭДС трансформации;

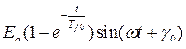 − ЭДС вращения.

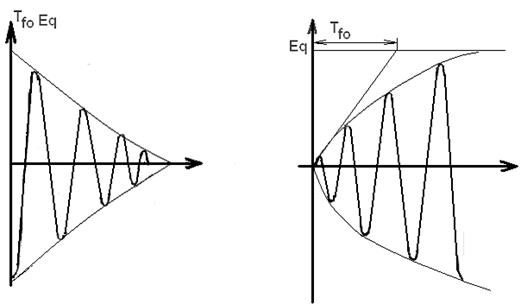
Рис. 8.7. Характер изменения составляющих ЭДС статора

При реальных значениях постоянных времени генераторов , или в относительных единицах 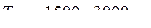 ЭДС трансформации в тысячи раз меньше ЭДС вращения, и поэтому в практике расчетов может не учитываться.
В этом случае 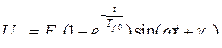 для фазы А.

Для машины с демпферными обмотками вводят: , при этом скорость нарастания ЭДС статора уменьшается.

Внезапное КЗ синхронной машины без демпферных обмоток

Ранее были рассмотрены вопросы определения периодической и апериодической составляющих тока КЗ в первый период и установившемся режиме короткого замыкания исходя из физических соображений. Представляется важным строго исследовать переходный процесс для любого момента времени и уточнить полученные ранее расчетные выражения на основе решения уравнений Парка−Горева для внезапного трехфазного КЗ на шинах синхронной машины  без демпферных обмоток.

Допущения:

1) режим симметричный ;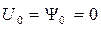

2) КЗ металлическое, т.е напряжение на выводах при КЗ равно нулю; ;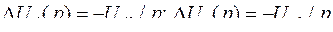

3) отсутствует АРВ и приращение ;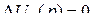

4) индуктивные сопротивления цепи статора намного больше  активных. Уравнения (8.7) с учетом допущений принимают вид:

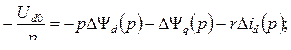
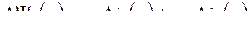
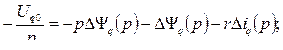
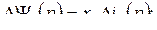                          (8.10)                      

                        .

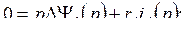
Решение системы (8.10) [9,15] с переходом к трехфазной машине: 

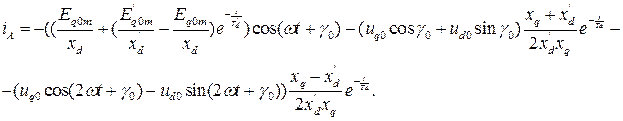
Характер тока статора при трехфазном КЗ приведен на рисунке 8.9.  

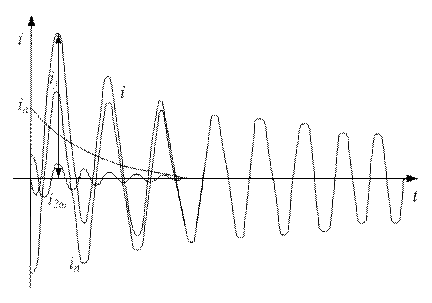
Рис. 8.9. Характер тока статора при трехфазном КЗ

На рисунке 8.9. 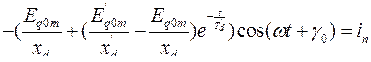− периодическая составляющая тока;

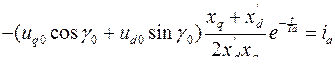− апериодическая составляющая тока;

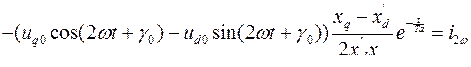− вторая гармоника.

Ток в обмотке возбуждения:

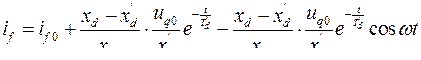            (8.12)    

ОСНОВНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА НЕСИММЕТРИЧНЫХ   

КОРОТКИХ ЗАМЫКАНИЙ