В теорії графів книжковим вкладенням називають вкладення графа в тривимірний простір. Таке вкладення має місце для довільного графа. Нагадаємо, що не кожен граф можна вкласти в площину. Книжкове вкладення являє собою набір півплощин, що мають одну і ту ж пряму в якості межі. Зазвичай потрібно, щоб вершини графа лежали на цій межі, а ребра зображувалися всередині сторінок так, щоб будь-яких два ребра не мали спільних точок, крім належних їм вершин. Книжкова товщина (або кількість сторінок) графа — це найменше число півплощин для всіх книжкових вкладень графа. Найбільше книжкове вкладення має товщину, рівну числу ребер графа. У максимальному книжковому вкладенні в кожній півплощини тільки одне ребро графа.

Макензі і Овербей вивчали застосування книжкової товщини у загальній алгебрі за допомогою графів, отриманих з дільників нуля скінченного локального кільця шляхом створення вершини для кожного дільника нуля і ребра для кожної пари значень, добуток яких дорівнює нулю (тобто з допомогою графів дільників нуля кільця). У своїй роботі [18] вчені помітили, що деякі вузли РНК приймають вигляд чотирьохсторінкового книжкового вкладення і зображуються у вигляді графів дільників нуля скінченних локальних кілець. Макензі і Овербей також припустили, що якщо описати структуру нуклеїнової кислоти у вигляді повного дводольного графа дільників нуля деяких кілець, то використовуючи властивості цих кілець і їх графів дільників нуля, можна буде зрозуміти структуру РНК, а потім описати і структуру ДНК. Наступний крок - запропонувати шляхи зміни цієї структури у людей, схильних до різних захворювань, і тим самим попередити їх виникнення.

Все це припущення, які поки ніхто не зміг ні підтвердити, ні спростувати. Пріоритетним завданням сучасної теорії кілець є дослідження, в тому числі і графів дільників нуля кілець, які можна буде застосувати не тільки для розвитку самої математики, але і в біології, медицині та інших науках.

ВИСНОВКИ

У кваліфікаційній роботі були розглянуті графи, вершинами яких є дільники нуля заданого скінченного кільця. Розглянуто необхідні для викладу матеріалу поняття: «кільце», «граф», «дільник нуля», «граф дільників нуля», «стиснений граф дільників нуля», побудовані приклади графів дільників нуля для різних скінченних кілець. Також було обґрунтовано значення даної теми. Розглянуті властивості кілець, графи дільників нуля яких мають певний тип: однорідні, ейлерові, дводольні, повні дводольні. Також були побудовані звичайні та стиснені графи дільників нуля для кілець конгруентності за модулем 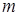, кільця верхньотрикутних матриць другого порядку над кільцем конгруентності за модулем 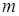. 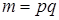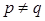Самостійно вдалось отримати загальний вигляд індексів для повного дводольного графа дільників нуля кільця конгруентності за модулем , де  і p , q - прості числа, а також побудувати графи дільників нуля для кілець, які є прямим добутком кілець конгруентності за модулем  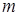та графи дільників нуля для нільпотентних кілець.

Результати можуть бути використані при читанні спецкурсів з алгебри, особливо з теорії кілець, для знайомства із задачами теорії графів, зокрема із книжковими вкладеннями графів, для ознайомлення із застосуваннями у інших галузях знань, зокрема в біології, генетиці.

ПЕРЕЛІК ПОСИЛАНЬ

1. Akbari S. When a zero-divisor graph is planar or a complete r-partite graph [Текст] / S. Akbari, H.R. Maimani, Yassemi

2. Akbari S.  On zero-divisor graphs of finite rings [Текст] / S. Akbari, H.R.Maimani - J. Algebra  314, 2007.

3. Akbari S. On the zero-divisor graph of a non-commutative ring [Текст] / S. Akbari, H.R. Maimani - J. Algebra  274, 2004.

4. Akbari S. On the zero-divisor graph of a commutative ring [Текст] / S. Akbari, H.R. Maimani - J. Algebra  274, 2004.

5. Anderson, The zero-divisor graph of a commutative ring. [Текст] /  D. Anderson, David F. and Livingston, S. Philip  - J. Algebra 217 ,1999.

6. Anderson D. Beck’s coloring of a commutative ring [Текст] /  D. Anderson , D. Naseer - Algebra 159, 1993.

7. Aihua Li Zero divisor graphs of upper triangular matrix rings [Текст] / Aihua Li and Ralph P. Tucci - 2013.

8. Beck I. Coloring of commutative rings [Текст] / Ivar Beck- J. Algebra 116 (1), 1988.

9. Belshoff R. Planar zero-divisor graphs [Текст] / R. Belshoff, J. Chapman - J. Algebra 316 (1), 2007.

10. Bollobas B. Graph theory: an introductory course [Текст] / Bela Bollobas- 1979.

11. Kuz’mina A.S. Nilpotent finite rings with planar zero-divisor graphs [Текст] /  A.S. Kuz’mina, Yu.N Maltsev -  Asian-European J. Math.1 (4), 565–574 (2008).

12. Кузьмина А.С. Описание конечных ненильпотентных колец, имеющих планарные графы делителей нуля [Текст] /  Кузьмина Анастасия Сергеевна- Дискретная математика 4, 2009.

13. Кузьмина А.С. О строении колец с планарными графами делителей нуля [Текст] / Кузьмина Анастасия Сергеевна - 2009.

14. Кузьмина А.С. Конечные кольца, нильпотентные графы которых являются однородными [Текст] / А.С. Кузьмина, Ю.Н. Мальцев - 2015.

15. Кузьмина А.С. Конечные кольца с полными двудольными графами делителей нуля [Текст] / А.С. Кузьмина, Ю.Н. Мальцев - 2012.

16. Кузьмина А.С., Finite rings with Eulerian zero-divisor graphs [Текст] / Кузьмина Анастасия Сергеевна  - J. of Algebra 2012.

17. Кузьмина А.С. Describing ring varieties in which all finite rings have

Hamiltonian zero-divisor graphs [Текст] / А.С. Кузьмина, Ю.Н. Мальцев - 2013

18. Thomas McKenzie Book embeddings and zero divisors [Текст] /  Thomas McKenzie, Shannon Overbay Ars -  Combinatoria, 2010.

19. Nazar H. Shuker The zero divisor ideal graph of the ring Z_N [Текст] / Nazar H. Shuker, Payman A. Rashed - 2015.

20. Weber D. Zero-Divisor Graphs and Lattices of Finite Commutative Rings[Текст] / David Weber -  2011.