Означення 3.7 Нільпотентом кільця 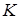 називають такий елемент 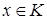, що .

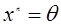Означення 3.8 Ідемпотентом кільця 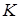 називають такий елемент 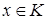, що .

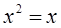Означення 3.9 Кільце називається нільпотентним, якщо у ньому не існує відмінного від нульового ідемпотента.

Приклад 3.6 Розглянемо кільце 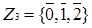. Так як нуль у будь-якому степені дорівнює нулю, то елемент  є і нільпотентом і ідемпотентом кільця 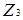. А так як елемент  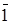 є ідемпотентом кільця, то кільце  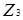не є нільпотентним кільцем за означенням.

Приклад 3.7  Розглянемо кільце 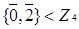. Елемент  є як нільпотентом, так і ідемпотентом за означенням, а елемент 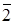 є тільки нільпотентом. Так як в кільці не існує ненульового ідемпотента, то дане кільце є нільпотентним.

Введемо означення нільпотентного графа кільця. Нехай R – довільне ассоціативне кільце і N(R) – множина нільпотентних елементів кільця R. Вершинами нільпотентного графа Γ_N(R) кільця R є елементи множини 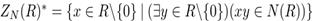, при цьому дві відмінні вершини  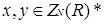з’єднані ребром тоді і тільки тоді, коли .

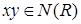Приклад 3.8 Розглянемо кільце .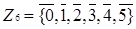

Граф дільників нуля такого кільця виглядає наступним чином:

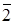
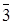
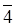
                              Рисунок 3.7  

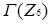
Множина нільпотентних елементів кільця 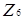 має вигляд 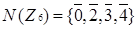, множиною вершин нільпотентного графа є множина 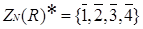. За означенням нільпотентного графа маємо:

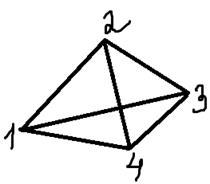
                                         Рисунок 3.8

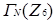
Із означень випливає, що граф дільників нуля Γ(R) є підграфом нільпотентного графа.

Означення 3.10  Однорідний граф – це граф, усі вершини якого мають одну й ту саму степінь. Степеню вершини називається число ребер графа, яким належить ця вершина.

Як бачимо із рис. 3.8, нільпотентний граф 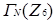 є однорідним.

     Наслідок 3.2 Якщо у кільці 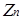 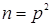і p – просте, то граф дільників нуля кільця буде повним й однорідним з p-1 вершинами.

     Приклад 3.9 Розглянемо кільце 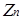, 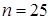. Граф дільників нуля кільця має вигляд:

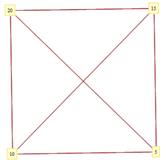
Рисунок 3.9

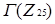
Аналогічно, для усіх 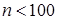 й рівних одному із наступних значень: 9,25 і 49 графи дільників нуля для кільця  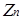будуть повними і однорідними.

     Приклад 3.10 Щоб навести приклад неоднорідного нільпотентного графа, розглянемо знову кільце 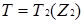. Його елементами є наступні 8 матриць:

.

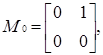
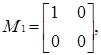
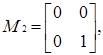
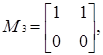
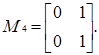
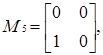
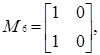
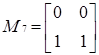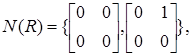
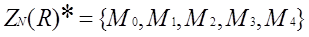
Побудуємо нільпотентний граф кільця :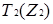

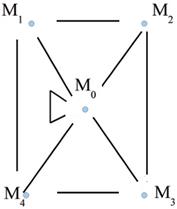
Рисунок 3.10

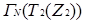
Як бачимо із рис. 3.10, граф 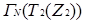 є неоднорідним, так як степінь вершини  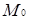більше степені всіх інших вершин нільпотентного графа.

     Теорема 3.6 Нехай R – довільне ненульове асоціативне скінченне кільце, що не є полем. Тоді наступні умови еквівалентні:

 (1) граф Γ_N(R) є повним, причому усі ненульові елементи кільця R є вершинами графа Γ_N(R);

 (2) кільце R є нільпотентним.

     Лема 3.3 Нехай R – довільне кільце і 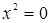 для усіх 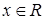. Тоді R - антикомутативне кільце.

Доведення. Нехай R – скінченне кільце, що задовольняє тотожності

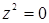.Тоді,  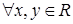виконується 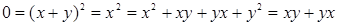. Звідси,  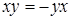для усіх .

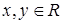     Означення 3.11 Альтернативним називають кільце, у якому кожна пара елементів породжує ассоціативне підкільце.

     Теорема 3.7 Нехай R – скінченне нільпотентне альтернативне кільце. Тоді граф Γ(R) є однорідним у тому і тільки у тому випадку, якщо R² = (0).

Доведення. Нехай R – скінченне нільпотентне альтернативне кільце з однорідним графом дільників нуля, 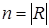 і k – індекс нільпотентності кільця R, 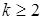. Зауважимо, що для будь якого ненульового елемента a ∈ R^k−1 має deg(a) = n − 2. В силу однорідності графа Γ(R) усі вершини цього графа мають степінь n−2. Доведемо, що кільце R задовольняє тотожності  x² = 0.

Припустимо, що у кільці R існує елемент b, такий, що b² = 0. Тоді вершина b в графі Γ(R) не суміжна з вершинами b і b + b² , тобто, deg(b) ≤ n − 3, чого бути не може. Отже, кільце R задовольняє тотожності x ²= 0 і за лемою 3.3 є антикомутативним. Доведемо, далі, що R² = (0). Припустимо протилежне, тобто що R²= (0). Тоді існують такі різні елементи 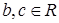, що 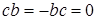. В цьому випадку вершина c не є суміжною з вершинами b і b + c, тобто deg(c) ≤ n − 3 < deg(a); протиріччя.

Отже, R² = (0). Обернене твердження очевидно.

     Наслідок 3.3 Нехай R – скінченне нільпотентне альтернативне кільце. Тоді граф Γ(R) є однорідним тоді і тільки тоді, коли кільце R асоціативне.

     Теорема 3.8 Нехай R – скінченне нільпотентне асоціативне за нулем кільце. Тоді граф Γ(R) є однорідним тільки у тому випадку, коли R² = (0).